tanaka_notes_on_oo-categories

AN INTRODUCTION TO 1-CATEGORIES

HIRO LEE TANAKA

Abstract. These are notes prepared for David Ben-Zvi's 2012 workshop on Categorical Representation Theory. I assume no knowledge of simplicial sets, or of categories enriched in spaces. I do assume people know what a category is, and what limits and colimits are.

As David wrote me, \I'd really like people to accept it as a shiny black box and not get too intimidated by the machine, rather to get a feel for what it's for, how it

1.Introduction

1.1.Some categories have spaces of morphisms. In algebraic topology, things become much easier when we treat the set of maps between X and Y as a space of maps

1

from X to Y . For instance, given two morphisms f0; f1 : X ! Y , it makes sense to ask whether there's a path between them { that is, whether the two maps are homotopic. This makes the fundamental group (and homotopy groups in general) easy to work with, and gives rise to incredibly useful notions like homotopy equivalence. The notion that the set of morphisms is a space is useful in other categories, like the category of chain complexes.1

1.1.1. Finding an appropriate language for such categories. Perusing through Maclane [Maclane72], you see immediately that there's a ton of useful category theory for usual categories. And we know from previous talks that things like the Barr-Beck theorem help us say great things about categories. (For instance, knowing that some mystery category C is all of a sudden a category of modules gives you a lot of information!) It would be wonderful if all the tools from set-enriched categories could transfer over to space-enriched categories.

But to fully embrace the topological, or homotopical nature of these categories, we need a new framework. For instance, any contractible space and the one-point space are homotopy equivalent spaces. But in the language of ordinary category theory, only the one-point space is a terminal object.

1.2. De nition of 1-category. I advocate that the correct framework for all this is the framework of 1-categories. At rst pass it's not clear that the de nition will t all our needs, but hopefully by the end of this talk, and the end of this week, you'll be convinced it's a good notion.

I'll give the de nition of an 1-category now. You won't know what a simplicial set is yet, but don't worry, I'll get there. I just want to leave this de nition on the board so that, as I go through the talk, you'll see some of the motivations as we plow forward.

De nition 1.1 (1-category). Let C be a simplicial set. Let ni be the simplicial set obtained from the n-simplex n by deleting the ith face and the interior. We say that C is an 1-category if any inner horn can always be lled. That is,

n /C

i ~>

~

~ ~ 9

n

for 0 < i < n, n 2. A functor f : C ! C0 is just a map of simplicial sets.

If this de nition remains cryptic, don't worry. For now let's talk about what a simplicial set actually is. I'll motivate it by observing the structure of categories. Then we'll talk about how this actually recovers a notion of a morphism space, how to go from a topologically enriched category to an 1-category, and how to de ne some of the usual notions from category theory (co/limits).

1For instance, homology is useful because it takes homotopies of maps of spaces to homotopies of maps of chain complexes. This is a consequence of the fact that the functor taking a space to its complex of singular chains is in fact a functor which is a continuous map on morphism spaces.

2

2. Categories as certain simplicial sets

The rst time I was introduced to simplicial sets, the de nition seemed a bit arbitrary. Let me make a few observations about categories to motivate the de nition of a simplicial set.

2.1. The simplices of a category. Let C be a category. What does this mean? Well, C has a set of objects.2 I'll denote this set as Ob C = C[0] and I'm going to draw the objects of C as vertices.

C[0] := Ob C

And of course for every pair of objects X0; X1 2 C[0] one also has a set of morphisms C(X0; X1). We will denote by C[1] the set of all morphisms:

And there is more structure { any category C has a composition rule, which is a map of sets

C(X1; X2) C(X0; X1) ! C(X0; X2):

In terms of pictures, this says that the following picture with edges f01; f12 can be lled to form a commutative triangle, with third edge f02 = f12 f01:

The composition rule.

This actually tells us two pieces of information at once { rst, it tells us whether a drawing of a triangle should be considered a commutative triangle. Second, it tells us that one can obtain a commutative triangle from two successive edges. We now separate out these two pieces of data. First, since we know what triangles are commutative, we will set

C[2] = fcommutative triangles in Cg:

The composition rule is something we'll ignore for the moment { as it turns out there will be no such rule in a quasi-category. So we'll come back to the data of two successive edges giving rise to a unique triangle in just a moment. Also, for the moment let me ignore the associativity rule of a category. I'll get back to that too.

By now you probably see a pattern. I drew C[0] as the set of objects in a category, which I think of as a collection of 0-simplices. I de ned C[1] as the set of morphisms,

2I'll assume C is small, since most categories we work with are essentially small.

3

which we've always drawn as arrows. So I've drawn elements of C[1] as a directed 1-simplex, and likewise an element of C[2] is a 2-simplex representing a commutative triangle. So I'm going to de ne

C[n] = fcommutative n-simplices in Cg:

Now I claim that some morphisms among the sets C[n], along with a property similar to the de ning property of 1-categories (De nition 1.1), completely characterize the idea of a category.

2.2. The simplicial relations. Let's say you have a commutative n-simplex. I'll write it as a string

One consequence of the associativity condition is that this string is enough for you to determine the n-simplex entirely. (As it turns out this will not be true for 1-categories.)

I want to note that there's a few natural ways to get a commutative (n 1)-simplex from this n-simplex. Namely, pick an object, and forget it, composing morphisms if necessary. For instance, forgetting the 0th object, we get

while forgetting the ith object for 0 < i < n, we get

Let's denote by di the map `forget the ith object.'

di : C[n] ! C[n 1]:

This exists for any 0 i n, so long as n 1. (There is no set C[ 1].) We'll call it the ith face map. This is because if you draw the n-simplex, di precisely picks out the face opposite the ith vertex. We can summarize these maps in the following diagram:

Going the other way, given an n-simplex, there's actually a way to canonically get an (n + 1)-simplex. Namely, you insert the identity morphism after the ith object:

We'll call this map

si : C[n] ! C[n + 1]

and call it the ith degeneracy map. Note there is a map for 0 i n. These maps can all be drawn as follows:

4

Moreover, if you think about what the maps si and di do, you can prove the following relations. I'll leave the veri cation as an exercise; it's very straightforward.

>

>

:

These are called the simplicial relations.

De nition 2.1 (Simplicial set). A collection of sets D[n], n 2 Z 0, together with maps

si : D[n] ! D[n + 1]; di : D[n] ! D[n 1]

for 0 i n, satisfying the simplicial relations, is called a simplicial set.

Exercise 2.2 (The category of simplicial sets). Let be the category whose objects arenite, non-empty, ordered sets, and whose morphisms are weakly order-preserving maps.

(1) Show that a simplicial set is the same thing as a functor

op ! Sets:

We let sSet denote the category of simplicial sets, where morphisms are given by natural transformations.

We denote by n the functor represented by the ordered set [n] = f0 < 1 < : : : < ng. This means

n[m] = forder-preserving maps [m] ! [n]g:

We call this the n-simplex.

(2) Show that there is a natural isomorphism of sets D[n] sSet( n; D).

=

(3)Write down the simplicial set corresponding to the horn ni .

(4)Let C; D be simplicial sets. We de ne a collection of sets (C D)[n] := C[n] D[n]. Show that (C D)[ ] naturally has the structure of a simplicial set.

(5)Show that sSet is enriched over itself. For instance, show that

sSet(C; D)[n] := sSet(C n; D)[0]

where sSet( ; )[0] is the set of natural transformations, de nes a simplicial set sSet(C; D) with the obvious face and degeneracy maps.

Example 2.3 (BG). Let G be a discrete group. Let BG be the simplicial set such that BG[k] = Gk. The face maps are given by

d0 : (g1; : : : ; gn) 7!(g2; : : : ; gn); dn : (g1; : : : ; gn) 7!(g1; : : : ; gn 1);

The degeneracy maps are given by inserting idG in various places. Note that a functor BG ! C picks out an object in C together with a group action.

5

2.3. Categories as a simplicial set with a hornlling condition. By design every category C gives rise to a simplicial set C[ ]. This simplicial set in fact satis es something very similar to the condition in De nition 1.1. First, let's let 12 be the diagram one obtains by taking a 2-simplex, then deleting the interior and the face opposite the 1st vertex of the 2-simplex. (This is the same data as two successive edges.) Then if the simplicial set C[ ] arises from a category, we can complete this `horn' into a full-blown 2-simplex: one can ll in the diagram

21 /

C

•?

•

• • 9!

2 :

Moreover this lling is unique, as indicated. This is due to the composition law { after all, given two morphisms f01; f12, there is only one way to compose them.

We can go further. Let in denote the diagram one obtains by taking an n-simplex, and deleting the face opposite the ith vertex (we delete the interior of the n-simplex as well). Then an easy exercise using the associativity law shows that we can ll such a horn in uniquely too, provided 0 < i < n:

n /C

i ~>

~

~ ~ 9!

n :

Staring at this commutative diagram and the diagram in De nition 1.1, you see that the only di erence is in the uniqueness of this lling.

2.4. What's it like to work in this setting? I want to take a break at this point. The only di erence between an ordinary/usual category and an 1-category is { I am not kidding you { this uniqueness property of how one can ll in horn. That's it. I'll go into the details of what this means for us in a second, but David wanted me to say what it's like to work in this setting, so let me comment on that in two ways.

2.4.1. As someone who just uses category theory. As I motivated earlier, we want to formulate classical theorems, and be able to prove them, for categories which have more homotopical avor. There are plenty of ways in which one can encapsulate the notion of a homotopical category, like model structures, enriching over spaces, or Segal spaces. But the question is: Can we write a Maclane-type tome of results using those other frameworks? No doubt we one day will, but we haven't. The only setting in which all the useful results from classical category theory have been translated into, and proven in, a homotopical setting is in the 1-category setting. What does this mean for you, practically? In a sense it means you can retain all the algebraic intuitions you had from classical categories and apply them to the 1-category setting. Adjunctions are more or less what you think they are, as are Kan extensions and all that.

6

2.4.2. As someone who wants to prove something in category theory. That being said, what's it like to work with an 1-category? The point is that simplices are just a nice way to encode homotopy-commutative diagrams, just as simplices are a nice way to encode some portion of a topological space. A category is a massive thing, just as a topological space is, but we can reduce the proof of most categorical statements to proofs about how the combinatorics of simplices behave.

Moreover, the lack of uniqueness means we often don't have a composition law. Given two successive edges X0 ! X1; X1 ! X2, all we know is that there exists some edges X0 ! X2 which we'd like to call the composition, but there is no `the' composition. This is the same issue that arises when one tries to de ne the fundamental group { there is no canonical way to compose two paths sharing an endpoint. Indeed, the willingness to depart from a strict composition law is one way in which this whole business becomes easier to deal with.3

2.5. Kan complexes are 1-groupoids are spaces. So what does this 'lack of uniqueness' mean for us? The interpretation I'll promote is that the simplices of an 1-category C are not to be interpreted as commutative diagrams anymore { they should be interpreted as homotopy commutative diagrams, together with prescribed homotopies between the various simplices of the diagram. Here's an example.

Exercise 2.4. Let W be a topological space. Let

Sing(W )[n] = Maps(j nj; W )

where j nj is the topological space corresponding to the standard n-simplex, and Maps is the set of continuous maps. Show that Sing(W )[n] de nes a simplicial set, where the face maps di are given by restriction of maps.

I claim that not only is Sing(W ) a simplicial set, it's also an 1-category. Here's an illustration in the most basic case. It's easy to see that the map 21 ! Sing(W ) corre-

sponds to a pair of maps a; b : j 1j [0; 1] ! W such that a(1) = b(0). And to nd

=

a map 2 ! Sing(W ) extending this is the same thing as nding a map j 2j ! W of spaces which restricts to a and b on the 0th and 2nd faces, respectively.

Filling the horn 21.

This is easy to do, and in fact there are many continuous maps j 2j ! W that ful-ll this condition.

So how do we interpret Sing(W ) as a type of category, and what does the nonuniqueness mean? The interpretation is that the 0-simplices of Sing(W ) are the objects.

3That being said, many times our 1-categories will arise from topologically enriched categories that do have an underlying composition, but as I've advocated, forgetting that structure and simply remembering the simplices of the category is what makes many proofs easier.

7

The 1-simplices { paths from one point to another { are the morphisms, and the higher simplices are homotopies of morphisms (and higher homotopies between these). For instance, a 2-simplex is a homotopy between two paths { the path obtained by concatenating the edges 0 ! 1 and 1 ! 2, and the path obtained by the edge of 2 which goes from 0 to 2. (Here, the numbers 0; 1; 2 are the vertices of 2.) Similarly, a 3-simplex is a homotopy between various 2-simplices.

This 1-category is very special, in that every morphism is invertible up to homotopy.

Exercise 2.5 (Groupoids). Suppose that C is not only a category, but also a groupoid. This means that every morphism has an inverse. Show that the associated simplicial set satis es the lling condition

for any horn { i.e., even when i = 0 or i = n.

Exercise 2.6 (1-groupoids, Kan complexes). Show that Sing(W ) satis es the lling condition

for any horn { i.e., even when i = 0 or i = n. This is the 1-analogue of a groupoid. We call any simplicial set satisfying this lling condition an 1-groupoid, or a Kan complex. (Both terms are used in the literature.)

De nition 2.7. Let @ n denote the simplicial set obtained by deleting the interior of the n-simplex. Let C be a Kan complex. We say that C is contractible if C is non-empty and one can always ll the following diagram:

Exercise 2.8. Show that if W is a contractible space, then Sing(W ) is a contractible Kan complex.

Exercise 2.9. Let Kan denote the full subcategory of sSet consisting of Kan complexes. Note that we have a functor

Sing : Spaces ! Kan:

Moreover, given any simplicial set, we have a functor called geometric realization which produces a topological space. This is done by gluing together the n-simplices of a simplicial set via the face maps di. We denote this functor

j j : Kan sSet ! Spaces:

Convince yourself that there is a natural homotopy equivalence j Sing W j ' W .

8

Remark 2.10. We don't have time to go into the details here, but as a philosophy, \Kan complexes are the same as topological spaces." More precisely, there is a Quillen equivalence between a model category of simplicial sets and a model category of topological spaces, where the model structure on simplicial sets has Kan complexes as brantco brant objects. From hereon, whenever I come across a Kan complex, I will pretend that it has the same mathematical worth as a topological space. I really wish I had more time to go into this, but this will have to do.

Remark 2.11 (Some bearings). By de nition we have the inclusions categories 1-categories sSet: groupoids Kan sSet:

2.6. Identity morphism and equivalences. For every object X 2 C[0] there is a canonical edge s0X 2 C[1]. We call this the identity morphism idX of X. We say that a morphism f : X0 ! X1 is an equivalence if there is a map g : X1 ! X0 and 2-simplices A; B 2 C[2] such that

All this means is that there's two homotopy commutative diagrams in C as follows:

Note that A and B don't just tell you that this diagram is homotopy commutative, they actually specify the homotopies f g idX1 and g f idX0 .

2.7. Morphism spaces. So how does one extract a `space' of morphisms from two vertices X0; X1 2 C[0] in an 1-category? There are two natural ways:

De nition 2.12 (Morphism spaces). Let X0; X1 2 C[0]. Then the right morphism space CR(X0; X1) is de ned to be the simplicial set whose n-simplices are maps u : n+1 ! C satisfying

(1)ujdn+1 n+1 7!X0:

(2)u(n + 1) = X1,

The left morphism space CL(X0; X1) is de ned to be the simplicial set whose n-simplices are maps u : n+1 ! C satisfying

(1)u(0) = X0,

(2)ujd0 n+1 = X1.

Example 2.13. For example, a vertex f 2 CL(X0; X1) = CR(X0; X1) is an edge in C with initial vertex X0 and nal vertex X1.

A 2-simplex e 2 CL(X0; X1) is a triangle whose 0th vertex is X0, and whose face opposite X0 is the degenerate edge s0X1. The triangle has two other edges, d1e and d2e, and one should interpret the 2-simplex e as a homotopy from the morphism d2e to the morphism d1e.

9

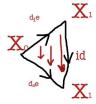
An edge e in CL(X0; X1) represents a triangle in C with a degenerate edge.

If you believe that Kan complexes are like morphism spaces, here's the reason I call the above a morphism space:

Proposition 2.14. CL(X0; X1) and CR(X0; X1) are both Kan complexes, provided that C is an 1-category. Moreover, their geometric realizations are homotopy equivalent spaces.

The last bit of the proposition tells us that it doesn't matter which model we use, CL or CR. Either safeguards all the homotopical information of the space of morphisms from X0 to X1.

Exercise 2.15. Let Sing(W )R(X0; X0) be the Kan complex of right morphisms from a point X0 2 W to itself. Let W be the based loop space of W based at X0. Construct a homotopy equivalence Sing( W ) ! Sing(W )R(X0; X0).

Now we can de ne what it means to be an initial or terminal object of C.

Remark 2.17. In general, wherever you see the word `unique' in classical category theory, in 1-category jargon, you should see the word `contractible.'

Exercise 2.18. Show any two initial objects are equivalent. Show any two terminal objects are equivalent.

3. Cones, limits/colimits.

I've tried to give a brief overview of the landscape of simplicial sets. Kan complexes are spaces, and 1-categories are, well, like imsy versions of categories. At the least they have a notion of morphism spaces, well-de ned up to homotopy equivalence.

It's absurd how much of math comes down to proving a statement about limits and colimits. But it's true. And the rst step in converting classical category theory to 1-category theory is to get a good grasp on what limits and colimits really are. We embark on this task now. For this, you need to know what a cone is.

3.1. Cones. If W is a topological space, we know what its cone is. It's most easily described as the space W [0; 1]= , where the equivalence relation collapses everything every point of the form (w; 0). In the world of simplicial sets, where every simplex has a direction, or an orientation, there are two kinds of cones one can make from a simplicial

10