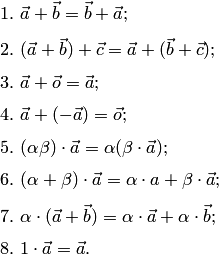шпоры матем (2)
.docx|
24.
Функция. Основные определения.Функция —
математическое понятие,
отражающее связь между элементами
множеств.
Можно сказать, что функция — это
«закон», по которому каждому элементу
одного множества (называемого областью
определения) ставится в соответствие
некоторый элемент другого множества
(называемого областью
значений).Функция Теперь можно дать более точное определениефункции: правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией. Из этого определения следует, что функция считается заданной, если: - задана область определения функции X ; - задана область значений функции Y ;- известно правило ( закон ) соответствия, причём такое, что для каждого значения аргумента может быть найдено только одно значение функции. Непрерывная и разрывная функции. Функция y = f ( x ) называется непрерывной в точке x = a, если :функция определена при x = a, т.e. f ( a ) существует;-существует конечный предел lim f ( x ) и x→a; f ( a ) = lim f ( x )x→a.Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a.Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией. Чётная и нечётная функции. Если для любого x из области определения функции имеет место: f ( x ) = f ( x ), то функция называется чётной; если же имеет место: f ( x ) = f ( x ), то функция называется нечётной. График чётной функции симметричен относительно оси Y, a график нечётной функции симметричен относительно начала координат. Периодическая функция. Функция f ( x ) - периодическая, если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции.Все тригонометрические функции являются периодическими. Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем ) функции. Функция может иметь несколько нулей. Например,
функция y = x ( x +
1 ) ( x3 )
имеет три нуля: x =
0, x = 1, x = 3.
Геометрически нуль
функции – это
абсцисса точки пересечения графика
функции с осью Х .
Монотонная функция. Если
для любых двух значений
аргумента x1 и x2 из
условия x2 > x1 следует f ( x2 )
> f ( x1 ),
то функция f ( x ) называется
возрастающей;
если для любых x1 и x2
из условия x2 > x1 следует f ( x2 ) < f( x1 ), то функция f ( x ) называется убывающей.
Функция, которая только возрастает
или только убывает,
называется монотонной.Ограниченная
и неограниченная
функции. Функция называется ограниченной, если существует
такое положительное число M,
что | f ( x ) | |
25. Точные верхняя и нижняя грани. Максимум и минимум функции. Определение! Функция y=f(x) называется ограниченной (сверху) снизу если существует такое (М) m при которой : m ≤ f(x) – ограничена снизу! Где m – нижняя грань! М ≥ f(x) – ограничена сверху! Где М – верхняя грань! Функция называетсяОграниченной если m ≤ f(x) ≤ М Точная верхняя грань – это наименьшая из верхних граней (супермум) supF(x) ; Точная нижняя грань – это набольшая из всех нижних граней (инфимум) inff(x); Если F(x) не ограничена Cверху supf(x) = + бескон. Снизу inff(x) = - бескон. Наибольшее
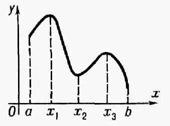
и наименьшее значения функции по
сравнению с её значениями в достаточно
близких точках. На рис. функция y =
f(x) имеет в точках х1 и х3> максимум,
а в точке х2> -
минимум. Точки М. и м. наз. точками
экстремума.
A - это max/ min для y = f(x) если выполняются условия
Обозначение! A = minf(x); x принадлежит X A = maxf(x); x принадлежит X ЗАМЕЧАНИЕ! В общем случае f(x) может иметь supf(x) \ inff(x) но может не иметь max \ min (у любой функции всегда есть sup \ inf ,но не всегда есть max и min.
|
26. Определение предела функции в точке. Свойства предела.
Точка a называется предельной точкой множества X, если в любой её окрестности есть хотя бы одна точка из множества Х, отличная от точки а (если есть хотя бы хотя бы одна, то таких точек будет очень много). Предельная точка может принадлежать множеству, а может и нет. X Определение
предела функции по Коши (через Число
А
Проколотая
Определение предела функции по Гейне (в терминах последовательностей). Число
Теорема (3.1) Определения предела функции в точке по Коши и по Гейне эквивалентны. Свойства пределов функции. 1°
Предел суммы/разности двух функций
равен сумме/разности их пределов: 2°
Предел произведения двух функций
равен произведению их пределов: 3°
Предел частного двух функций равен
частному их пределов, при условии, что
предел знаменателя не равен нулю: 4°
Константу можно выносить за знак
предела: 5°
Предел степени с натуральным
показателем равен степени предела:
|
|
21.
Монотонная последовательность —
это последовательность,
элементы которой с увеличением номера
не убывают, или, наоборот, не возрастают.
Подобные последовательности часто
встречаются при исследованиях и имеют
ряд отличительных особенностей и
дополнительных свойств. Последовательность
из одного числа не может считаться
возрастающей или убывающей.{an}-
произвольная последовательность.{an}
возрастает если an<an+1,{an}
убывает если an>an+1,{an}
не
возрастает если an≥
an+1,{an}
не
убывает если an≤
an+1.ТЕОРЕМА
:Всякая
неубывающая (невозрастающая) ограниченная
сверху (снизу) последовательность
имеет
предел!
Понятие
Монотонной последовательности. Пусть
имеется множество Теорема: limn стремится к ∞ (1+1/n)n= ℮ (важный предел!)
|
22.
{an}
произвольная последовательность!Выберем
множество номеров. Например :
последовательность {a5a6a7
}.Составленная
последовательность из чисел
последовательн ости{an}
называется
Подпоследовательностью!
Примечание!
Обязательно члены подпоследовательности
должны находиться в том же порядке
убывания / возрастания что и в начальной
последовательности!Подпоследовательностью
Теорема Больцано — Вейерштрасса
ТЕОРЕМА :Из всякой ограниченной последовательности можно выделить сходящуюся последовательность. Пусть
предложена последовательность
точек пространства
и пусть эта последовательность ограничена, то есть
где Тогда из данной последовательности можно выделить подпоследовательность
которая сходится к
некоторой точке пространства Теорему Больцано — Вейерштрасса в такой формулировке иногда называют принципом компактности ограниченной последовательности.
|
23.Фундаментальная последовательность Последовательность точек метрического пространства называется фундаментальной или последовательностью Коши, если её элементы становятся ближе друг к другу с увеличением номера. Последовательность
точек Свойства Любая последовательность, имеющая предел, является фундаментальной. Критерий Коши для сходимости функций : Числовая последовательность сходится тогда и только тогда, когда она фундаментальна. Если
фундаментальная последовательность Критерий Коши Пусть
задана числовая последовательность
{xn}.
Эта последовательность сходится тогда
и только тогда, когда для любого
числа ε >
0 существует номер N такой,
что при всех n > N и
любых натуральных m выполняется
неравенство
Итак, взятая последовательность удовлетворяет критерию Коши, поэтому она сходится (имеет предел).
Поскольку
|
||
|
27. Определение предела функции в точке. Односторонние пределы. Теорема существования предела функции в точке. Говорят,
что функция y=f(x)
имеет пределом число a
при x f(a+0)= f(a-0)= Говорят,
что функция y=f(x)
имеет пределом число a
при x Определение по Гейне и определение по Коши эквивалентны. Теорема.
|
28. Монотонные функции. Функция y=f(x) называется:
Теорема. Если функция y=f(x) монотонна на (a;b), то в каждой точке x0 из этого интервала существуют односторонние пределы справа и слева. Теорема.
Если функция y=f(x)
не убывает (не возрастает) на (a;
x0),
где x0 29. Первый и второй замечательные пределы. Предел сложной функции. 1.
Первый замечательный предел
2.
Второй замечательный предел
3.
4.
5.
Замечание: 1.
2. 3.
4.
Предел сложной функции y=f(x)
– функция и z=g(y)
– функция, причем функция g
определена на множестве значений
функции f
(f(x) Теорема.
Если существует предел g(y)
при y
|
30. Бесконечно малые функции. Классификация бесконечно малых функций. Эквивалентные бесконечно малые. Функция
Основные свойства бесконечно малых функций: 1° Сумма конечного числа б.м функций является функцией б.м. 2° Произведение б.м функции на ограниченную есть функция б.м. 3° Произведение двух б.м функций есть функция б.м. 4° Произведение б.м функции на константу является б.м функцией. 5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м. 6°
Функция
Теорема.
Пусть b
– предел функции y=f(x)
в точке a:
Бесконечно малые функции одного порядка. Пусть
Бесконечно малые функции более низкого и высокого порядков. Если
Если
Если
Эквивалентные (равносильные) бесконечно малые функции. Если
Таблица
эквивалентных б.м. функций при
Теорема. Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них. Верно и обратное утверждение. Теорема. Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка. |
||
|
31.Определение непрерывности функции в точке. Функция f(x) называется непрерывной
в точке Следствие. ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ. Определение устранимого разрыва первого рода. В
точке Определение неустранимого разрыва первого рода (точка скачка функции). В
точке Определение разрыва второго рода (бесконечный разрыв). В
точке
|
32. Локальные свойства непрерывных функций: 1.
если функция f(x) непрерывна в точке 2.
если функция f(x) непрерывна в точке 3.
если функции f(x) и g(x) непрерывны в
точке 4.
если функция F(y) непрерывна в точке 33.Глобальные св-ва Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём. Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения. Областью
значений функции Если
функция Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна. Монотонная
функция на
отрезке Если
функции
|
34. Определение производной функции в точке. Пусть
функция f(x) определена
на промежутке (a;
b), Когда
последний предел принимает конкретное
конечное значение, то говорят о
существовании конечной
производной в точке.
Если предел бесконечен, то говорят,
чтопроизводнаябесконечна
в данной точке.
Если же предел не существует, то
и производная
функции в этой точке не
существует.Функцию f(x) называют дифференцируемой
в точке Если
функция f(x) дифференцируема
в каждой точке некоторого промежутка (a;
b), то функцию
называют дифференцируемой на этом
промежутке. Таким образом, любой
точке x из
промежутка (a;
b) можно
поставить в соответствие значение
производной функции в этой точке Операция нахождения производной называется дифференцированием. Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.Геометрический смысл производной.Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x№ 0, причем x+D x О (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x).Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел limD x® 0f (D x) = f 0, который равен углу, образованному касательной с положительным направлением оси OX. Справедливо утверждение: Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции. Тогда уравнение касательной к кривой f(x) в точке x0 имеет вид y = f(x0)+f'(x0)(x-x0)
Формула
нахождения производной сложной
функции.
|
||
|
35.
Функция Δf(x0) = A(x0)(x - x0) + ω(x - x0), (1) где ω(x - x0) = о(x - x0) при x → x0. Отображение Для значения дифференциала функции f принято обозначение df или df(x0), если требуется знать, в какой именно точке он вычислен. Таким образом, df(x0) = A(x0)h. Приращение
где
функция
В
силу того, что второе слагаемое
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике. Для приближенного вычисления значения функции применяется следующая формула:
|
36.Применение дифференциального исчисления (Правило Лопиталя.Формула Тейлора).
Правило Лопиталя – раскрытие неопределенностей вида 0/0, беск/беск. f(x), g(x) дифференцируемы в проколотой окрестности т. Х0 (Х0 – б<x< Х0 + б, х!= Х0). Limf(x) = 0 (при x-> Х0), limg(x) = 0 (при x-> Х0) (limf(x) = +беск(-беск) (при x-> Х0), limg(x) = +беск(-беск) (при x-> Х0). Тогда, если g’(x) != 0 и существует lim (f’(x)/ g’(x)) = A (при x-> Х0) конечный или бесконечный, то существует и lim (f(x)/ g(x)) = A (при x-> Х0) = lim (f’(x)/ g’(x)) = A (при x-> Х0) = А. Если при этом существует f’(Х0), g’(Х0), то А = f’(Х0)/ g’(Х0). Замечания: Правило Лопиталя верно, если выполнены все условия теоремы Имеют место примеры, когда lim (f’(x)/ g’(x)) = A (при x-> Х0) не существует, а lim (f(x)/ g(x)) (при x-> Х0) существует. Вывод: правило Лопиталя дает достаточное условие существования предела. Если f’(x) и g’(x) удовлетворяют тем же условиям, что и функции f(x), g(x), то правило Лопиталя можно применять повторно. Формула Тейлора Теорема.
y
= f(x),
x
= Х0
ϵ (а;в) из R,
имеет все производные до порядка n
включительно, тогда функция f(x)
представима в виде:
Lim 0((x - Х0)n)/ (x - Х0)n=0. Замечание: Многочлен Тейлора из формулы Тейлора определен единственным образом, т.е. единственным образом определены коэффициенты многочлена Тейлора. 37. Локальный экстремум функции. Лемма Ферма. Необходимое и достаточное условия внутреннего экстремума. 1.Условие монотонности функции Теорема: Пусть f(x) – функция, непрерывная на [a;b] и дифференцируемая на (a;b). Для того, чтобы функция f(x) возрастала (убывала) на (a;b) достаточно, чтобы для любого х ϵ (a;b) для возрастания: f’(x)>0; для убывания: f’(x)< 0. 2.Условие внутреннего экстремума y = f(x) –функция, определенная на (a;b) из R, т. Х0 ϵ (a;b) называется точкой локального максимума (локального минимума), а значения называются локальным максимум (локальным минимумом), если найдется окрестность т. Х0 , целиком лежащая в (a;b), в каждой точке которого выполнено неравенство f(x)<= f(Х0) (f(x) >= f(Х0)). Если f(x)< f(Х0) (f(x) > f(Х0)) для всех x != Х0 , x ϵ (Х0 – E; Х0 + E), то т. Х0 называется точкой строгого локального максимума (локального минимума). Точки locmin и locmax называются точками локального экстремума, а значение функции в этих точках – локальным экстремумом. Лемма Ферма: Если f(x), определенная на (a;b) из R имеет локальный экстремум в т. и дифференцируема в т.х0, то производнаяf’(x0) = 0. Замечания: Лемма Ф. дает необходимое условие только внутреннего экстремума функции, т.е. такого экстремума, что f(x) определена в целой окрестности т.х0 (x ϵ (Х0 – E; Х0 + E) из (a;b), E> 0). Лемма Ф. дает лишь необходимое условие, но не достаточное. х ϵ (a;b), х0 – точка locextrf(x), то f’(x0) = 0, либо f’(x0) не существует. (необходимое условие locextr) f(x) непрерывна в т. Х0 ϵ (a;b), то f’(x0) не существует либо f’(x0) = 0, тогда т.х0 будет т. locextr функции f(x), если при переходе через т.х0 знак производной функции f(x) меняется. х0 – точка loсmax, если слева от х0 f’(x) > 0, справа f’(x) < 0. х0 – точка loсmin, если слева от х0 f’(x) < 0, справа f’(x) > 0. (достаточное условие locextr)
|
1.Понятие неопределенного интеграла Функция дифференциального исчисления: нахождение производной или дифференциала данной функции. Функция интегрального исчисления: по данной производной или дифференциалу нужно найти функцию. Говорят, что F является первообразной по отношению к функции f, если F’(x) = f(x) для х ϵ (a;b). Операция нахождения первообразной по данной функции называется интегрированием. Операция интегрирования, в отличие от операции дифференцирования, многозначна. Теорема. Пусть F1 и F2 – первообразные к f из (a;b), тогда существует постоянная С такая, что F1(x) – F2(x) = C, х ϵ (a;b). Совокупность всех первообразных F по отношению к f из (a;b) называется неопределенным интегралом от функции f на (a;b).
Теорема. Справедливы соотношения:
39.Определенный интеграл Римана. Формула Ньютона-Лейбница. Разобьем [a;b] точками a=x0< x1< x2< … <xn – b liϵ [xi-1; xi], i = 1,2,…,n. xi
= xi
- xi-1;
i = 1,2,…,n. f(li)
Lim
Для того, чтобы f(x) была интегрируема достаточно, чтобы на этом отрезке непрерывна или имена на этом отрезке конечное число точек разрыва I рода – кусочно-непрерывная функция. Если f(x) непрерывна на [a;b], то она имеет первообразную ∫f(x) dx = F(x) +C
Геометрически определенный интеграл – площадь криволинейной трапеции, ограниченной линиями: y=f(x), y=0,x=a, x=b. 39.Определенный интеграл Римана. Формула Ньютона-Лейбница. Разобьем [a;b] точками a=x0< x1< x2< … <xn – b liϵ [xi-1; xi], i = 1,2,…,n. xi
= xi
- xi-1;
i = 1,2,…,n. f(li)
Lim
Для того, чтобы f(x) была интегрируема достаточно, чтобы на этом отрезке непрерывна или имена на этом отрезке конечное число точек разрыва I рода – кусочно-непрерывная функция. Если f(x) непрерывна на [a;b], то она имеет первообразную ∫f(x) dx = F(x) +C
Геометрически определенный интеграл – площадь криволинейной трапеции, ограниченной линиями: y=f(x), y=0,x=a, x=b.
|
||
|
11. 1.Векторы. Операции над векторами. Свойства операций. 1) Величины, которые характеризуются только числовым значением, называются скалярными. Величины, которые определяются своим числовым значением и направлением, называются векторными. Всякую векторную величину в физическом пространстве геометрически можно изобразить отрезком определенной длины и определенного направления (направленный отрезок). 2) Вектором АВ называется направленный отрезок, имеющий начало в точке А и конец в точке В. 3) Модулем или длиной вектора АВ называется длина отрезка АВ( |АВ|= АВ) 4) Вектор, начало и конец которого совпадают, называется нулевым, его направление выбирают произвольно. 5) Два вектора a и b называются равными, если: 1) их длины равны (|а|=|b|); 2) векторы параллельны, то есть расположены на параллельных или совпадающих прямых; 3) их направления совпадают (вектора сонаправлены). Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Сложение
векторов. Пусть
Ту
же сумму можно получить иным способом.
Отложим от точки О векторы
Вычитание
векторов. Разностью
Если
векторы
Таким
образом, если на векторах
Умножение
вектора на число. Произведением вектора
1)
11.2.2)
Очевидно,
что при
Построим,
например, векторы Свойства линейных операций над векторами
Для
любых векторов
Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.
Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.
Коллинеарные и компланарные вектора. 1) Векторы a и b называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Т1: Для того, чтобы векторы a и b были коллинеарны, необходимо и достаточно, чтобы они были пропорциональны. 2) 3 вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Т2: Для того чтобы векторы a, b, с были компланарны, необходимо и достаточно, чтобы один был линейной комбинацией 2-х других (с = αа + βb).
10.Теорема Кронекера-Капелли существования решения системы линейных уравнений.
Теоре́маКро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
Теорема Кронекера-Капелли . Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и ` A совпадают, т.е. r(A) = r( ` A) = r. Для множества М решений системы имеются три возможности: 1) M = Æ (в этом случае система несовместна); 2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной ); 3) M состоит более чем из одного элемента (тогда система называется неопределенной ). Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (m ³ n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.
|
16..Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых на плоскости. Угол между двумя прямыми. Допустим, на графике изображены две пересекающиеся прямые а1 и а2 с уравнениями k1x+b1 и k2x+b2 соответственно. Угол между прямой а2 и Ox – о1, угол между прямой а2 и Ox – о2, а угол между прямыми а1 и а2 – о. Тогда k1 = tg (o1), а k2 = tg (o2). Прямая cc1 проходит через точку пересечения прямых а1 и а2 и || Ox. Угол о2 = о+о1 => о = о2-о1. Tg (o) =tg (o2) – tg (o1) = (tg (o2) – tg (o1))/ (1 + tg (o2)*tg (o1)). Получается формула угла между прямыми: tg (o) = (k2 – k1)/(1+k2*k1), при этом o != п/2 и 0 <= o<= п. Замечания:
Условия параллельности и перпендикулярности двух прямых на плоскости.
Если а1 || а2, то угол между ними о = 0 =>tg (o) = 0 =>k1 = k2; Еслиa1перпен. а2, то угол между ними о = п/2 =>k1*k2 = -1;
Прямые ||, если А1/A2 = B1/B2; Прямые перпен., если A1*A2 + B1*B2 = 0; Дополнения:
17.Нормальное уравнение прямой.OZперпен. l, |OZ| = r, r≥0 ∟(OZ;Ox) = α MNперпен. Ox, т.M (x;y) – произвольная, принадлеж. Прямой l. NKперпен. OZ, MJперпен. NK ∟MNJ = ∟ZON = α; |OZ| = OK+KZ = r, KZ = MO =>r = OK + MO; ∆MON: MJ = MN* sinα = y* sinα; MN = y ∆OKN: OK = ON* cosα = x* cosα; ON = x. R = x*cosα + y*sinα =>х* cosα + у*sinα – r = 0 – нормальное уравнение прямой. Приведение общего уравнения прямой к нормальному виду. Ax + By + C = 0 |: (+-√A2+B2) Ax/(+-√A2+B2) + By/(+-√A2+B2) + C/(+-√A2+B2) = 0. Если C< 0 => “+”, если C> 0 => “-”. Расстояние от точки до прямой.-
l: х* cosα + у*sinα – r = 0, r>=0 M0 (x0,y0) d – расстояние от т. M0 до прямой l. d = | х0* cosα + у0*sinα – r|
20. Бесконечно малые и бесконечно большие последовательности. Говорят, что последовательность бесконечно малая, если ее предел равен 0.
Последовательность {an} называется бесконечно большой положительной (отрицательной), если для любого E>0 найдется такой номер, зависящий от E, что для всех элементов больше этого номера an>E и an<-E. Замечание: последовательности, стремящиеся к бесконечности не причисляются к сходящимся. Пусть последовательность {an} – бесконечно большая и все an!=0, тогда последовательность {1/ an} – бесконечно малая. Предельный переход и арифметические операции. Лемма – вспомогательное утверждение, требущее доказательства. Лемма: последовательность {an} имеет своим пределом число а тогда, и только тогда, когда предел (an-a) ({an-a}) – бесконечно малая.
Предельный переход и неравенства
13.Скалярным
произведением двух
ненулевых векторов
|
18. Числовая последовательность. Основные определения. {an}n=1+∞ nϵN, anϵR Говорят, что задана числовая последовательность {an}, если каждому натуральному n поставлено в соответствие вещественное число. А1, а2, …, аn,.. – члены бесконечной числовой последовательности. {an} задана формулой общего члена, если задана формула. an= f (n), nϵN Последовательность также может быть задана в следующем виде:
Замечание: Арифметическая и геометрическая прогрессии являются числовыми последовательностями. Последовательность называется ограниченной сверху, если найдется такое вещественное число M, при котором an<= M. Существует MϵR ɄnϵN: an<=M. Последовательность ограничена снизу, если существует mϵR, что для всех nm<= an Последовательность ограничена, если существует M, m ϵR, что ɄnϵN: a<= ɄnϵN:<=M 0<1/n<=1 – нижняя граница не достигается ни при каком натуральном n ! an=n, an>=1 – ограничена снизу an=-n, an>=-1 – ограничена сверху an=(-1)n – не ограничена нигде Последовательность называется постоянной, если все члены последовательности равны между собой Суммой 2х последовательностей (и разностью соответственно)называется последовательность, общий член которой представляет собой сумму общих членов anи bn. Свойства:
19. Предел числовой последовательности. Свойства (включая арифметические операции и неравенства). Lim (при n→∞) an = a. Если для ɄЕ>0 существует N(E) ϵN (найдется NϵN (зависящее от Е)), что для всех n>N(E) будет выполняться следующее: | an -a|<E – все элементы попадают в эпсилон-окрестность т. А Простейшие свойства предела последовательности
(lim an=A)=>(существует c ϵR, что | an |<=c ɄnϵN) !!!обратное утверждение неверно: не всякая последовательность ограниченная сходится.
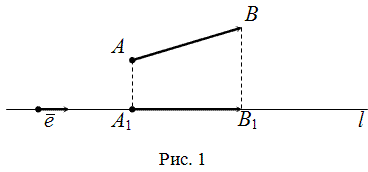
12. Проекция вектора на ось. Разложение вектора по ортам декартовой системы координат.
Проекцией
вектора
Проекция вектора Координаты вектора Пусть
задана прямоугольная декартова система
координат (ПДСК)
Определение
Координатами
вектора
Величина
Система ортов (или базисная система векторов) - это система единичных векторов осей координат. Орт
координатной оси
12.2.Для
любого вектора Если
вектор
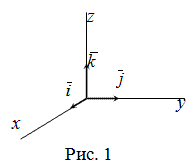
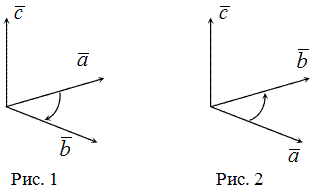
Три некомпланарных
вектора Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка
векторов
Тройка
векторов
|
||

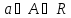
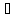 R,
a
– предельная точка множества Х, y=f(x),
x
R,
a
– предельная точка множества Х, y=f(x),
x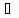 X.
X.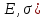 .
.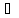 R
является пределом функции y=f(x),
x→a
(
R
является пределом функции y=f(x),
x→a
(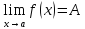 ),
если для любого Е>0 найдется такая
),
если для любого Е>0 найдется такая
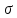 ,
что для х
,
что для х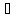 X,
х
X,
х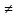 a:
|x-a|<
a:
|x-a|< => |f(x)-A|
<E.
=> |f(x)-A|
<E.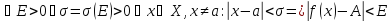
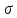 -окрестность
точки a.
-окрестность
точки a.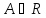 является пределом функции y=f(x),
x→a,
x
является пределом функции y=f(x),
x→a,
x X,
если для любой последовательности
{xn},
xn
X,
если для любой последовательности
{xn},
xn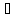 X,
xn
X,
xn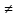 a,
n
a,
n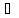 N,
xn
N,
xn a
(n
a
(n ∞),
последовательность функций f(xn)→A.
∞),
последовательность функций f(xn)→A.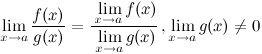
 а
дробь в знаменателе при n →∞
стремится к нулю, её предел равен 3.
а
дробь в знаменателе при n →∞
стремится к нулю, её предел равен 3. справа (слева), если для любой
последовательности точек {xn}
справа (слева), если для любой
последовательности точек {xn} a
(n
a
(n )
таких, что xn>a
справа или xn<a
слева, будет выполнено: {f(xn)}
)
таких, что xn>a
справа или xn<a
слева, будет выполнено: {f(xn)}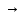 A
(n
A
(n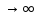 )
(См. определение по Гейне)
)
(См. определение по Гейне) – правый предел <= Односторонний
предел
– правый предел <= Односторонний
предел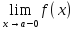 – предел слева <= Односторонний
предел
– предел слева <= Односторонний
предел справа (слева), если для любого E>0
найдется
справа (слева), если для любого E>0
найдется
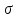 ,
что для всех x
,
что для всех x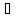 D(y)
σ= σ(E)>0
a<x<a+
σ (правая полуокрестность),
D(y)
σ= σ(E)>0
a<x<a+
σ (правая полуокрестность),
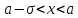 (левая полуокрестность) => |f(x)-A|<E
(См. определение по Коши)
(левая полуокрестность) => |f(x)-A|<E
(См. определение по Коши)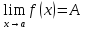 существует тогда, и только тогда, когда
сущ-т левый предел функции в точке,
правый предел функции в точке и они
между собой равны.
существует тогда, и только тогда, когда
сущ-т левый предел функции в точке,
правый предел функции в точке и они
между собой равны.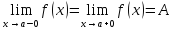
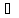 (a;b),
и ограничена сверху (снизу), то функция
имеет предел слева (справа) в точке
x0.
(a;b),
и ограничена сверху (снизу), то функция
имеет предел слева (справа) в точке
x0.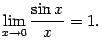

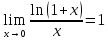
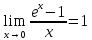
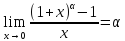
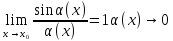 – написано под
– написано под
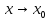
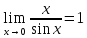

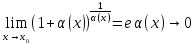 – написано под
– написано под
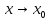
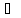 Y),
то функция z=g(f(x)),
то функция z
называется сложной функцией (композиция
функций, суперпозиция функций). При
этом z:x
Y),
то функция z=g(f(x)),
то функция z
называется сложной функцией (композиция
функций, суперпозиция функций). При
этом z:x R.
R.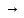 A
A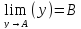 ,
где y=f(x)
и
,
где y=f(x)
и
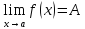 ,
то существует и
,
то существует и
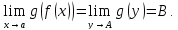
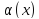 называется бесконечно малой функцией
(б.м.ф.) при
называется бесконечно малой функцией
(б.м.ф.) при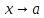 (или в точке
(или в точке
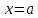 ),
если
),
если
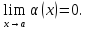
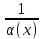 ,
обратная к б.м функции
,
обратная к б.м функции
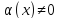 ,
есть функция бесконечно большая. Верно
и обратное.
,
есть функция бесконечно большая. Верно
и обратное.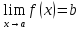 .
Тогда заданную функцию можно представить
в виде
.
Тогда заданную функцию можно представить
в виде
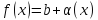 ,
где
,
где
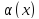 - б.м функция. Верно и обратное
утверждение.
- б.м функция. Верно и обратное
утверждение.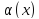 и
и
 называются б.м одного порядка малости
при
называются б.м одного порядка малости
при
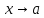 ,
если
,
если
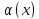 является б.м более высокого порядка
при
является б.м более высокого порядка
при
 ,
чем
,
чем
 ,
а
,
а
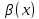 -
б.м. более низкого порядка по сравнению
с
-
б.м. более низкого порядка по сравнению
с
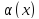 :
:

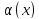 -
б.м. низшего порядка малости при
-
б.м. низшего порядка малости при по сравнению с
по сравнению с
 .
.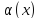 называется б.м. порядка k
по сравнению с
называется б.м. порядка k
по сравнению с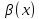 при
при
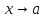 .
.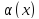 и
и
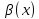 называются
эквивалентными или равносильными
б.м. одного порядка при
называются
эквивалентными или равносильными
б.м. одного порядка при
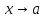 :
:
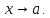
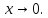
 Предельные равенства для эквивалентных
б.м. функций.Теорема.
Предел отношения двух б.м. функций
Предельные равенства для эквивалентных
б.м. функций.Теорема.
Предел отношения двух б.м. функций
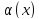 и
и
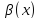 при
при равен пределу отношения эквивалентных
им б.м. функций
равен пределу отношения эквивалентных
им б.м. функций
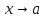 ,
то есть верны предельные равенства:
,
то есть верны предельные равенства:
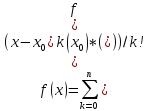 - многочлен Тейлора.
- многочлен Тейлора.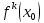 -
производная в т.
-
производная в т.
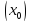 порядка k,
k
= 1,2,3,..,n.
порядка k,
k
= 1,2,3,..,n.
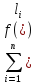 (xi
- xi-1)
– интегральная сумма
(xi
- xi-1)
– интегральная сумма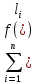 (xi
- xi-1)
(при max(xi
- xi-1)
-> 0)при существует и конечен, то он
называется определенным
интегралом Римана.
(xi
- xi-1)
(при max(xi
- xi-1)
-> 0)при существует и конечен, то он
называется определенным
интегралом Римана.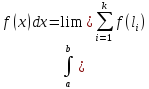 (xi
- xi-1)
(при max(xi
- xi-1)
-> 0) (a-нижний предел интегрирования,
b-верхний предел интегрирования, f(x) –
функция, интегрируемая по Риману на
[a;b].
(xi
- xi-1)
(при max(xi
- xi-1)
-> 0) (a-нижний предел интегрирования,
b-верхний предел интегрирования, f(x) –
функция, интегрируемая по Риману на
[a;b].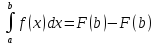 -формула
Ньютона-Лейбница
-формула
Ньютона-Лейбница
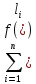 (xi
- xi-1)
– интегральная сумма
(xi
- xi-1)
– интегральная сумма (xi
- xi-1)
(при max(xi
- xi-1)
-> 0)при существует и конечен, то он
называется определенным
интегралом Римана.
(xi
- xi-1)
(при max(xi
- xi-1)
-> 0)при существует и конечен, то он
называется определенным
интегралом Римана.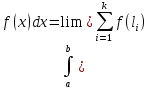 (xi
- xi-1)
(при max(xi
- xi-1)
-> 0) (a-нижний предел интегрирования,
b-верхний предел интегрирования, f(x) –
функция, интегрируемая по Риману на
[a;b].
(xi
- xi-1)
(при max(xi
- xi-1)
-> 0) (a-нижний предел интегрирования,
b-верхний предел интегрирования, f(x) –
функция, интегрируемая по Риману на
[a;b]. -формула
Ньютона-Лейбница
-формула
Ньютона-Лейбница