
- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •Приведённая ниже таблица показывает связь между множествами и случайными событиями.
- •Теория множеств
- •2 Решение типовых задач
- •2) Используем формулу де Моргана
- •Глава 2 Классическое вероятностное пространство.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§3 Задачи для самостоятельного решения
- •§2 Решение типовых задач Задача 1
- •Демонстрационная задача №1
- •Задача 2
- •Демонстрационная задача №2
- •Решение
- •Задача 3
- •Демонстрационная задача №3
- •Решение:
- •Вычисление числовых характеристик.
- •Вычислим вероятности попадания случайных величин в указанные области.
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Приложение
- •Основные свойства функции распределения f(X)
- •Основные непрерывные распределения
§2. Решение типовых задач.
Задача 1.
Случайным образом набирают пятизначный номер телефона.
Найти вероятности событий:
А = все цифры различны
В = все цифры нечётные и различные
С = все цифры чётные, но первая цифра не «о»
Решение:
Опыт: набор пятизначного номера
0,1,2,…,9
Имеем размещения с повторениями из 10 по 5 это элементарные исходы опыта
n()
= A 105
= 10
5
–
число всех исходов опыта
n(А) – число размещений из 10 по 5 без повторений.
n(A)
= A105 =
10*9*8*7*6
P(A)
= n(A)/n()=
10*9*8*7*6 /10*104 =0,3024
1,3,5,7,9
Только из этих цифр может состоять пятизначный номер.
n(B)
= P =
5! (перестановки из 5 элементов)
P(B) = n(B)/n()= 5! /10*9*8*7*6 = 0,0012
Будем рассуждать так:
|
|
|
|
|
|
4 5 5 5 5
0,2,4,6,8- данное множество.
По правилу умножения имеем: первая цифра выбирается из {2,4,6,8}, т.е. 4 способа, а
остальные, т.к. имеем уже 5 цифр - 5 способов.
 =
=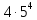
P(C)= =
=
Задача 2.
На входную дверь поставили четырёхзначный кодовый замок. Бомж не знает кода, но пытается открыть дверь. Найти вероятности следующих событий:
1). A={дверь открыли с первой попытки}
2). B={дверь открыли со второй попытки при условии, что стало известно о том, что все числа чётные}
3). С={открыли с пятой попытки, но при этом стало известно, что первая цифра «5» и все цифры различные}
Решение:
1). Опыт: Набор четырёх цифр из множества {0,1,2,3,4,5,6,7,8,9}. Элементарный исход – размещение из 10 по 4 с повторениями.
n(Ω)=104;
n(A)=1 (т.к. только один верный код);
P(A)=
2). Опыт: Набор четырёх цифр из множества {0,2,4,6,8}
n(Ω)=54 (размещения с повторениями)
n(B)=1 (только один верный исход)
P(B)= =
=
3) Так как первая цифра известна, то опыт заключается в том, что из цифр {0,1,2,3,4,6,7,8,9} выбирают различные три цифры, т.е. имеем размещения из 9 по 3 без повторений.
n(Ω)=
n(C)=1
P(C)=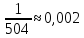
Задача 3.
На полке в один ряд стояли: 3 красных, 5 белых и 2 синих шара. Случайным образом шары переставили. Найти вероятности событий:
1). A={на первом месте стоит красный шар, на втором месте – синий, на третьем месте – белый шар}
2). B={шары одного цвета стоят рядом}
Решение:
Опыт: перестановка шаров. Элементарные исходы – перестановки с повторениями.
n(Ω)=P10(3,
5, 2)=
1). По условию задачи мы уже знаем, какие шары заполнили первое, второе и третье места. У нас осталось: 2 красных, 4 белых и 1 синий шар. Размещаем эти шары на семи местах (перестановки с повторениями).
n(A)=P7(2,
4, 1)=
P(A)=
2). Будем рассуждать так: имеем три неделимых группы, группа красных, группа белых и группа синих шаров. Будем переставлять эти группы.
n(B)=3!=6
P(B)= =0,00238
=0,00238
Задача 4.
Десять студентов ( пять юношей и пять девушек) случайным образом садятся в ряд.Найти вероятности следующих событий:
1). A={юноши сидят на чётных, а девушки на нечетных местах}
2). B={два друга и две подруги сидят рядом}
Решение.
Опыт: перестановки из десяти человек
n(Ω)=10!
1). {1,3,5,7,9} {0,2,4,6,8}
Нам нужно сделать перестановки и в множестве нечётных, и в множестве чётных чисел. По правилу умножения получим:
n(A)=5! 5!
5!
P(A)
=
2). Рассуждаем так: отделим данные две пары, а оставшихся шесть студентов переставим: 6!
Так как в парах не определен порядок, то нужно учесть перестановки в парах.
n(B)=2!⋅2!⋅6!
P(B)=
Замечание.
Если предметы распределяются по кругу, то число перестановок определяется по формуле:
(n-1)! [Формула циклических перестановок]
Задача 5.
В тесте 10 заданий и 4 варианта ответов (один верный). Студент случайным образом в каждом задании зачеркнул один ответ. Найти вероятности событий:
1). A={все правильные}
2). B={правильные в 1, 3 и 7 заданиях}
3). C={нет правильных}
4). D={хотя бы один правильный}
Решение:.
Опыт: выбор ответа в каждом задании. Элементарный исход – размещение из 4 по 10 с повторениями.
n(Ω)=410
1). n(A)=1
P(A)=
2). Из рассмотрения убираем три задания, и имеем уже размещение из 3 по 7 с повторениями (три неправильных).
n(B)=37
P(B)=
3) Имеем размещение с повторением из 3-х неверных ответов по 10 заданиям.

 0,0563
0,0563
4)
Заметим, что =C
=C
p(D)=1 –P(C)=1-0,0563=0,94368
Задача 6. Демонстрационная типовая задача на схему урн.
В урне 10 шаров: 3 красных, 5 синих, 2 белых. Случайным образом выбираем 4 шара. Найти вероятности следующих событий:
A = {все синие}
B = {не менее двух красных}
C = {два красных и два белых}
D = {хотя бы один синий}
Решение:
Опыт: Выбор 4-х шаров из 10. Элементарные исходы – сочетание из 10 по 4.
Число
всех исходов: n(Ω)=
n(A) – число сочетаний из 5 по 4
n(A)
=
 =
=
p(A)
=
 =
= =
=
Событие B= {не менее двух красных} представляет сумму событий:
 ={ровно
два красных} и
={ровно
два красных} и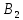 ={ровно
три красных}
={ровно
три красных}
Число исходов благоприятствующих Bопределяется по формуле:
n(B)=n(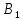 )+n(
)+n( )
)
n(B)= +
+ (используется правило произведения)
(используется правило произведения)

 =
=


n(B)=3
Р(В)= =
= =1/3
=1/3
n(C)=
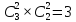
p(C)=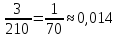
Рассмотрим противоположные события:
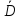 ={нет
синих}
={нет
синих}
n( )=
)=
p( )=
)= =
=
Тогда:
p(D)=1-p( )=
)=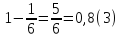
Задача 7
В финал танцевального конкурса было отобрано 10 человек, при этом:
5 человек из Москвы, 3 человека из Петербурга, 1 человек из Костромы, 1 человек из Ярославля. Для телевизионного шоу случайным образом (выбор компьютера) были выбраны 5 человек. Найти вероятности следующих событий:
A = {Кострома и Ярославль попали}
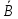 =
{хотя бы один из Петербурга попал}
=
{хотя бы один из Петербурга попал}
Решение:
Опыт: Выбор 5 человек из 10.
Элементарные исходы – сочетания из 10 по 5.
Число всех исходов:
n(Ω)= =252
=252
n(A) = 1
 =
=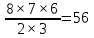
p(A)=
Рассмотрим противоположное событие:
 ={нет
представителей Петербурга}
={нет
представителей Петербурга}
n( )
=
)
= =21
=21
p(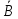 )=
)=
p(B)
= 1 -p(⌐B)=1-
Замечание:
nразличных предметов случайным образом
распределяются поSзанумерованным ящикам таким образом,
чтобыK-й ящик содержал
ровно предметов
(
предметов
(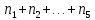 =n)
=n)
Тогда число всех элементарных исходов данного опыта определяется по формуле:
(*)
n(Ω)=
Задача 15





