
- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •Приведённая ниже таблица показывает связь между множествами и случайными событиями.
- •Теория множеств
- •2 Решение типовых задач
- •2) Используем формулу де Моргана
- •Глава 2 Классическое вероятностное пространство.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§3 Задачи для самостоятельного решения
- •§2 Решение типовых задач Задача 1
- •Демонстрационная задача №1
- •Задача 2
- •Демонстрационная задача №2
- •Решение
- •Задача 3
- •Демонстрационная задача №3
- •Решение:
- •Вычисление числовых характеристик.
- •Вычислим вероятности попадания случайных величин в указанные области.
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Приложение
- •Основные свойства функции распределения f(X)
- •Основные непрерывные распределения
Решение:
Т К Х и У независимы, то P{(X=xi)∙ (Y=yj)}=P{X=xi}∙ P{Y=yj}
Т.к. распределение компонент нам известно, то составим таблицу распределения двумерной случайной величины (Х;У):
|
х
у |
0 |
1 |
2 |
|
0 |
¼ |
3/16 |
1/16 |
|
1 |
3/16 |
9/64 |
3/64 |
|
2 |
1/16 |
3/64 |
1/64 |
Вычислим значения данных случайных величин в разных точках.
Z=X+Y
Z(0;0)=0
(p{Z=0}=0,25);Z(0;1)=1
(p{Z=1}= ):Z(0;2)=2
(p{Z=2}=
):Z(0;2)=2
(p{Z=2}= );
);
Z(1;0)=1
(p{Z=1}=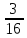 );Z(1;1)=2
(p{Z=
);Z(1;1)=2
(p{Z= );Z(1;2)=3
(p{Z=3}=
);Z(1;2)=3
(p{Z=3}= );
);
Z(2;0)=2;
(p{Z=2}=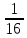 );Z(2;1)=3;
(p{Z=3}=
);Z(2;1)=3;
(p{Z=3}= );Z(2;2)=4;
(P{Z=4}=
);Z(2;2)=4;
(P{Z=4}= )
)
P{Z=0}=1/4; P{z=1}=3/16+3/16=6/16=3/8;
P{Z=2}=1/16+9/64+1/16=17/64
P{Z=3}=3/64+3/64=6/64=3/32
Таким образом, ряд распределения случайной величины Z=X+Y имеет вид:
|
Z |
0 |
1 |
2 |
3 |
4 |
|
P |
¼ |
3/8 |
17/64 |
3/32 |
1/64 |
Z=X∙ Y
Z(0;0)=0
(p{Z=0}=0,25);Z(0;1)=0 (p{Z=0}= ):Z(0;2)=0
(p{Z=0}=
):Z(0;2)=0
(p{Z=0}= );
);
Z(1;0)=0
(p{Z=0}= );
Z(1;1)=1 (p{Z=
);
Z(1;1)=1 (p{Z= );
Z(1;2)=2 (p{Z=2}=
);
Z(1;2)=2 (p{Z=2}= );
);
Z(2;0)=0;
(p{Z=0}= );
Z(2;1)=2; (p{Z=2}=
);
Z(2;1)=2; (p{Z=2}= );
Z(2;2)=4; (P{Z=4}=
);
Z(2;2)=4; (P{Z=4}= )
)
P{Z=0}=0,25+ +
+ +
+ +
+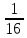 =0,75
=0,75
p{Z=
p{Z=2}= +
+ =
= =
=
P{Z=4}=
Таким образом, ряд распределения случайной величины Z=X∙Y имеет вид:
|
Z |
0 |
1 |
2 |
4 |
|
P |
0,75 |
9/64 |
3/32 |
1/64 |
Вычисление числовых характеристик.
Для выполнения контроля вычислим необходимые числовые характеристики данных случайных величин Х и У.
M[X]= =
= =
=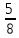 ;
M[X2]=
;
M[X2]= =
= =
= ;D[X]=M[X2]-
;D[X]=M[X2]- =
=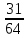
M[Y]= D[Y]=
D[Y]=
(В данном примере законы распределения случайных величин Х и У равны и , следовательно, равны и числовые характеристики. Если бы задания величин были различными., то необходимо вычислить числовые характеристики случайной величины У по соответствующим формулам).
Теперь вычислим числовые характеристики с найденных выше случайных величин.
Z=X+Y
M[Z]=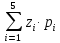 =
=
 =1,25
=1,25
Cделать
контрольную проверку:M[X+Y]=M[X]+M[Y]
= =1,25
=1,25
D[Z]=
M[z2]-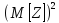 M[Z2]=
M[Z2]=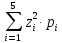 =
= →D[Z]=
→D[Z]=
Cделать
контрольную проверку:D[X+Y]=D[X]+D[Y]
= (по
свойству независимых случайных величин);
(по
свойству независимых случайных величин);
Z=X∙Y
M[Z]= =
=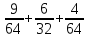 =
=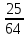
Cделать
контрольную проверку:M[X∙Y]=M[X]∙M[Y]=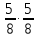 =
=
Вычислим вероятности попадания случайных величин в указанные области.
P{X+Y∈[1;3]}=P{Z=1}+P{Z=2}+P{Z=3}
=
P{X∙Y∈(0
;4)}=
P{Z=1}+P{Z=2}= =
=

§3. Задачи для самостоятельного решения
Задача 1
Детали на производстве сортируются на 4 группы по величине отклонений от номиналов двух существенных параметров.
Отклонения ранжируются. Ранги Х и У отклонений могут принимать лишь значения 0 и 1.Распределение двумерной случайной величины (Х;У) задано таблицей :
|
Х
У |
0 |
1 |
|
0 |
0,94 |
0,01 |
|
1 |
0,02 |
0,03 |
Найти коэффициент корреляции R[ X;Y]=xy ,называемый ранговым.
Ответ: xy=0,66
Задача 2
Х и У –индикаторы событий А и В, означающих положительные ответы соответственно на вопросы
и социологической анкеты. По данным социологического опроса двумерная случайная величина (Х;У) имеет следующую таблицу распределения :
|
Х
У |
0 |
1 |
|
0 |
0,3 |
0,1 |
|
1 |
0,2 |
0,4 |
Здесь положительному ответу присвоен ранг 1, отрицательному -0.
Найти коэффициент корреляции R[ X;Y]=xy
Ответ: xy=0,408
Задача 3
Х и У независимые случайные величины заданы таблицами:
|
Х |
1 |
2 |
3 |
|
Р |
0,5 |
0,1 |
0,4 |
|
У |
0 |
2 |
|
Р |
0,5 |
0,5 |
Найти таблицу распределения двумерной случайной величины (Х;У).
Найти центр распределения М(mx; my).
Найти значение функции распределения в точках М1(1,1);
М2(2,1); М3(3;3).
4)Найти вероятности выполнения неравенств:Х+У>2; Х2+У2≤5
5)Найти R[X;Y].
6)
Найти регрессии
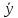 (x)
и
(x)
и
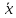 (y)
(y)
7)Описать закон распределения случайной величины Z=X+Y.
Ответ:1)
|
Х
У |
0 |
1 |
|
1 |
0,25 |
0,25 |
|
2 |
0,05 |
0,05 |
|
3 |
0,2 |
0,2 |
2)М(1,9;
1); 3)F(M1)=0;
F(M2)=0,25;
F(M3)=0,6;
4)P{X+Y>1}=0,75;
P{X2+Y2≤5}=0,55;
5)R[X;Y]=0;
6) (x)=1;
(x)=1;
 (y)=1,9.
7)
(y)=1,9.
7)
|
Z |
1 |
2 |
3 |
4 |
5 |
|
P |
0,25 |
0,05 |
0,45 |
0,05 |
0,2 |
В задачах 4; 5;6; 7 найти:
Найти безусловные законы распределения компонент Х и У.
Найти центр распределения M(mx;;my).
Проверить условие зависимости Х и У.
Найти числовые характеристики: Dx; Dy; х; у; K[X;У] (момент корреляции).Полученные результаты записать в виде корреляционной матрицы: К=
 ,
заметим, чтоK[X;Y]=K[Y;X].
,
заметим, чтоK[X;Y]=K[Y;X].Найти коэффициент корреляции R[X;Y] и определить степень линейной зависимости между Х и У .
Найти значение функции распределения F(x;y) в указанных точках:
Найти вероятности попадания значения (Х;У) в указанные области:
Найти условные законы распределения Х/У, У/Х.
Найти регрессии
 (у)
и
(у)
и (х).
(х).
Задача 4
|
х
У |
-1 |
0 |
2 |
|
-1 |
0,3 |
0.2 |
0 |
|
1 |
0.1 |
0,1 |
0.3 |
6) М1(0,5; 0); М2(0;1); М3(2;2).
7)Р{X*Y≤1}=?
Ответ:1)
|
Х |
-1 |
1 |
|
Р |
0,5 |
0,5 |
|
У |
-1 |
0 |
2 |
|
Р |
0,4 |
0.3 |
0,3 |
M(0;0,2)
Х и У зависимы
)К=

R[X;Y]≈0,64
F(M1)=0,3; F(M2)=0,5; F(M3)=0,7;
Р{X*Y≤1}=0,7.
8)
|
Y/X |
-1 |
0 |
2 |
|
P{Y/X=-1} |
0,6 |
0,4 |
0
|
|
P{Y/X=1} |
0,2 |
0,2 |
0,6
|
 (х).=
(х).=
Задача 5
|
Х
У |
0 |
2 |
|
1 |
0.25 |
0,25 |
|
2 |
0,05 |
0,05 |
|
3 |
0,2 |
0.2 |
6)М1(1;1); М2(2;1); М3(3;3);
7)Р{X+Y3}; P{X2+Y2≤4}
Ответ:2)М(1,9;1);3)
Х и У независимы;4)К= ;
6)F(M1)=0;
F(M2)=0,25
;
6)F(M1)=0;
F(M2)=0,25
F(M3)=0,6;
7)
Р{X+Y3}=0,45;
P{X2+Y2≤4}=0,3;8)P{Y/X}=P{Y};P{X/Y}=P{X}9) (у).=1,9
(у).=1,9
Задача 6
|
Х
У |
1 |
2 |
|
2 |
0,3 |
0.5 |
|
3 |
0,1 |
0,1 |
6)М1(3;2); М2(4;1); М3(2,5;1.5); 7)Р{Х+У≤4}
Ответ:2)М(2,2;
1,6);3)Х и У зависимы;4) К= ;5)R[X;Y]=-0,1
;5)R[X;Y]=-0,1
6)P(M1)=0,3;
P(M2)=0;
P(M3)=0,3;
7)
Р{Х+У≤4}=0,9;9) (у)=
(у)=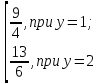
Задача
7
|
Х У |
0 |
2 |
3 |
|
1 |
0,1 |
0,2 |
0.1 |
|
2 |
0,2 |
0 |
0,2 |
|
3 |
0 |
0.1 |
0,1 |
6)М1(2;2); М2(3;3);М(1;3);7)Р{Y≤X2}
Ответ:
2)М(1,8;1,8);3)Х и У зависимы;4)К= 5)R[X;Y]≈0,17
5)R[X;Y]≈0,17
6)F(M1)=0,3;
F(M2)=0,5;
F(M3)=0;
7)Р{Y≤X2}=0,7;9) (х).=
(х).=
Задача 8
Заполнить таблицу распределения двумерной случайной величины (Х;У), если известны значения функции распределения в заданных точках:
F(0;0)=0,2; F(1;2)=0,3; F(3;1)=0,4; F(5;0)=0,7; F(3;2)=0,6.
Найти а) P{X+Y≤2}; b)M[X+2*Y+X*Y]
|
X
Y |
-1 |
1 |
|
-1 |
|
|
|
2 |
|
|
|
4 |
|
|
Ответ:
|
х
у |
-1 |
1 |
|
-1 |
0.2 |
0,1 |
|
2 |
0,2 |
0.1 |
|
4 |
0.3 |
0.1 |
а) P{X+Y≤2}=0,5 b) M[X+2*Y+X*Y]=0,2.









