§2 Решение типовых задач Задача 1

Дано: Двумерная случайная величина (Х;У) задана таблицей распределения.

1. Найти безусловные законы распределения компонент Х и У.

2. Найти центр распределения M(m_x;;m_y).

3. Проверить условие зависимости Х и У.

4. Найти числовые характеристики: D_x; D_y; _х; _у; K[X;У] (момент корреляции).Полученные результаты записать в виде корреляционной матрицы: К=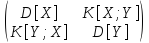, заметим, чтоK[X;Y]=K[Y;X].

5. Найти коэффициент корреляции R[X;Y] и определить степень линейной зависимости между Х и У .

6. Найти значение функции распределения F(x;y) в указанных точках:М₁(0,1; 1,7); М₂(0;0); М₃(0;3).

7. Найти вероятности попадания значения (Х;У) в указанные области: а) P{X+Y>1}; б)P{y²≤4*(X+1)}.

8. Найти условные законы распределения Х/У, У/Х.

9. Найти регрессии (у) и(х).

Закон распределения случайной двумерной случайной величины задан таблицей (добавленные строка и столбец будут добавлены в процессе решения задачи)

Демонстрационная задача №1

Х У	1	2	Р{X=xi}
-1	0,3	0.1	0,4
0	0,2	0,1	0,3
2	0.1	0,2	0,3
P[Y=yj}	0,6	0.4	1

Решение:

1. Безусловные законы распределения:P{X=x_i} =,…i=1, 2, 3.

Х	-1	0	2
Р	0,4	0,3	0.3

P{Y=y_j}=, j=1,2.

Y	1	2
P	0,6	0.4

2.Центр распределения:

М(m_x;m_y)=?

M[X]=_i∙ x_i=-1*0,4+0*0.3+2*0.3=0,2

М[Y]=_j∙ y_j=1*0,6+2*0,4=1,4

М(0,2;1,4)

3.Проверка зависимости (независимости) случайных событий.

Если Х и У независимые случайные события , то должно выполняться равенство для всех значений х и у: P{(X=x_i)∙ (Y=y_j)}=P{X=x_i}∙ P{Y=y_j}

Если. хотя бы один раз равенство не выполняется, то Х и У зависимы.

Рассмотрим следующие вероятности:

P{(X=-1)∙ (Y=1)}=0,3; P{X=-1}=0,4; P{Y=0,6}0.4∙ 0,60,3

Х и У зависимые случайные величины.

4.Числовые характеристики и корреляционная матрица

D[X]=M[X²]-(m_x)²; M[X²]=_i³∙ p_i=0,4+0+1,2=1,6 D[X]=1,6-(0,2)²=1,56;

_x=1,25

D[Y]=M[Y²]-(m_y)²; M[Y²]=_j∙ ²p_j=0,6+1,6=2,2 D[Y]=2,2-(1,4)²=0,24

_y==0,49.

K[X,Y]=M[X∙Y]-m_x*m_y; M[X∙Y]=∙ x_i∙y_j=

=-1∙1∙0,3+(-1)∙2∙0,1+0∙1∙ 0,2+0∙ 2∙ 0,1+2∙ 1∙ 0,1+2∙ 2∙ 0,2=0,5

K[X,Y]=0,5-0,2∙ 1,4=0,22K[X,Y]=0,22

Корреляционная матрица: К=

5.Коэффициент корреляции

R[X,Y]=R[X,Y]=0,36;R[X,Y]0,36

(Связь ощутимая, но не линейная)

6.Вычисление значений функции в заданных точках.

F(M₁)=F(0,1;1,7)=P{(X0,1)*(Y1,17)}=0,3+0,2=0,5

F(M₂)=F(0;0)=P{(X0)∙ (Yy)}=0

F(M₃)=F(0;3)=P{(X0)∙ (Y3)}=0,3+0,1=0,4

7.Нахождение вероятности попадания значений случайной величины в указанные области.

а) P{X+Y>1}=0,1+0,1+0,2=0,4

b)P{Y²≤4*(X+1)}=0,2+0,1+0,2+0,1=0,6

Y²=4(x-1)

2

1

-1

2

0

X+y=2

(Для вычисления данных вероятностей можно сделать чертёж или непосредственно перебирать все варианты)

8.Условные законы распределения

P{X=-1/Y=1}==0,3/0,6=1/2

P{X=0/Y=1}==0,2/0,6=1/3

P{X=2/Y=1}==0,1/0,6=1/6

P{X=-1/Y=2}=0,1/0,4=1/4

P{X=0/Y=2}=0,1/0,4=1/4

P{X=2/Y=2}=0,2/0,4=1/2

X	-1	0	2
P{X/Y=1}	½	1/3	1/6
P{X/Y=2}	¼	¼	1/2

Аналогично составляем условный закон распределения Y/X

Y	1	2
P{Y/X=-1}	0,3/0,4=3/4	0,1/0,4=1/4
P{Y/X=0}	0,2/0,3=2/3	0,1/0,3=1/3
P{Y/X=2}	0,1/0,3=1/3	0,2/0,3=2/3

9.Условные математические ожидания (регрессии)

2

y

M[X/Y=y_j]=(y)=

1

x

(y)= (регрессия х по у)

-

0,75

M[X]=0,2

Заметим, что M[X]=0,2 (на одном чертеже в системе координат(у0х)

постройте график регрессии и математическое ожидание М[X])

M[Y/X=x_i]=(x)=

M[Y]=1,4

0

(x)=(регрессия у по х)

-1

2

Заметим, что M[Y]=1,4. (на одном чертеже в плоскости(х0у) постройте график регрессии и математического ожидания M[Y]

Вывод: Х оказывает малое влияние на У, а У оказывает большое влияние на Х (эти выводы вы можете сделать , анализируя построенные графики)