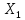- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •Приведённая ниже таблица показывает связь между множествами и случайными событиями.
- •Теория множеств
- •2 Решение типовых задач
- •2) Используем формулу де Моргана
- •Глава 2 Классическое вероятностное пространство.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§3 Задачи для самостоятельного решения
- •§2 Решение типовых задач Задача 1
- •Демонстрационная задача №1
- •Задача 2
- •Демонстрационная задача №2
- •Решение
- •Задача 3
- •Демонстрационная задача №3
- •Решение:
- •Вычисление числовых характеристик.
- •Вычислим вероятности попадания случайных величин в указанные области.
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Приложение
- •Основные свойства функции распределения f(X)
- •Основные непрерывные распределения
Задача 22
Очень наблюдательный, занимающийся кражей предметов искусства вор. который, вероятно, знает хорошо статистику, заметил, что частота. с которой охранники обходят музей., равномерно распределена между 15 и 60 минутами.
Следовательно., если Х обозначает время в минутах до появления охраны, то дифференциальная функция f(x) имеет вид:
f(x)=
Постройте графики функций: f(x) и F(x).
Найдите вероятность того., что охранник появится в течение 35 минут после появления вора.
Найдите вероятность того, что охрана не появится в течение 30 минут.
Найдите вероятность того. что охрана появится между 35 и 45 минутами после прихода вора.
Ответ:1)F(x)= 2)P{X>35}=5/9;
3)P{X≤35}=4/9;
2)P{X>35}=5/9;
3)P{X≤35}=4/9;
4)P{30≤X≤45}=1/3.
Задача 23
Вес тропического грейпфрута, выращенного в краснодарском крае, нормально распределённая случайная величина с неизвестным математическим ожиданием m и дисперсией равной 0,04.Агрономы знают, что 65% фруктов весят меньше, чем 0,5 кг..
Найдите ожидаемый вес случайно выбранного фрукта.
Ответ:P{X0,5}=0,5+( )≈0,65m≈0,578
)≈0,65m≈0,578
Задача 24
Предположим. что в течение года цены на товар некоторой фирмы подчинялись нормальному закону распределения с математическим ожиданием , равным 48 у.е.., и стандартным отклонением, равным 6. Чему равна вероятность того, что в случайно выбранный день обсуждаемого периода цена за товар была: 1)более 60 у.е.;
2)ниже 60 у.е.; 3)выше 40 у.е.; 4)между 40 и50 у.е.?
Ответ:1)P{X>60}=0,5-( ≈0,02275;
2)P{X60}=1-P{X60}≈0,97725;
≈0,02275;
2)P{X60}=1-P{X60}≈0,97725;
3)P{X>40}≈0,90824;
4)P{40X50}=( -(
-( ≈0,53750
≈0,53750
Задача 25
Чтобы овощное блюдо было вкусным., содержание в нём паприки
не должно отклоняться от указанного в рецепте более чем на 50 гр.
Точность, с которой хозяйка следует рецептуре, характеризуется
стандартным отклонением х.
Выяснить, сколько % домохозяек делают вкусное блюдо, если =20?
Ответ:P{X-m50}=2*( ≈0,9898%
≈0,9898%
Задача 26
Молодой предприниматель решил изготавливать значки на закупленном оборудовании. Средний вес одного значка 55 кг.
Найти среднее квадратическое отклонение х , если10% значков имеют вес больше 60 гр. (Х-вес значка; Х N(m;))
Ответ: ≈3,84
Глава 9 Функция случайной величины
§1 Основные определения и понятия
Пусть
 – дискретная случайная величина,
заданная рядом распределения:
– дискретная случайная величина,
заданная рядом распределения:
|
|
|
|
|
|
… |
|
… |
|
|
|
|
|
|
|
… |
|
… |
|
Пусть
 – неслучайная функция:
– неслучайная функция:
(каждому
возможному значению случайной величины
 ставится в соответствии
одно значение
случайной величины
ставится в соответствии
одно значение
случайной величины
 ).
).
Все
значения случайной величины
 вычисляем по формуле:
вычисляем по формуле: ,
,
при
этом

Если
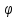 строго возрастает, то получаем ряд
распределения для
строго возрастает, то получаем ряд
распределения для :
:
|
|
|
|
… |
|
|
|
|
|
… |
|
так
как

Если
строго убывает, то

Если
функция
 имеет интервалы монотонности, то если
имеет интервалы монотонности, то если ,
то в таблице заносим одно значение, а
соответствующие вероятности складываются.
,
то в таблице заносим одно значение, а
соответствующие вероятности складываются.
Если
 непрерывная случайная величина
непрерывная случайная величина ,
причем
,
причем монотонно возрастающая непрерывно
дифференцируемая функция, то
монотонно возрастающая непрерывно
дифференцируемая функция, то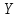 – тоже непрерывная случайная величина.
– тоже непрерывная случайная величина.
Если
 – распределения случайной величины,
то
– распределения случайной величины,
то

(
 – функция обратная для функции
– функция обратная для функции )
)
Таким
образом, если
 функция плотности с.в.
функция плотности с.в. ,
то
,
то
(1)
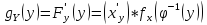
Если
 строго убывает, то
строго убывает, то
(2)

Объединив (1) и (2) получаем:
если
 строго монотонная функция, то для
нахождения функции плотности с.в.
строго монотонная функция, то для
нахождения функции плотности с.в. используем формулу:
используем формулу:
 где
где

Если
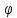 – функция не монотонна, то разбиваем
множество возможных значений
– функция не монотонна, то разбиваем
множество возможных значений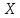 на интервалы монотонности
на интервалы монотонности ,
, ,
… ,
,
… , и на каждом интервале находим обратную
функцию
и на каждом интервале находим обратную
функцию ,
то где плотность случайной величины
,
то где плотность случайной величины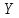 :
определяется в виде суммы:
:
определяется в виде суммы:
Полезная информация
Если
 имеет функцию плотности
имеет функцию плотности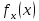 ,
а
,
а ,
то закон распределения с.в.
,
то закон распределения с.в. не меняется и при этом:
не меняется и при этом: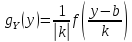
При
решении задач на нахождение плотности
 можно придерживаться следующей схемы.
можно придерживаться следующей схемы.
Дано
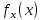

Найти