
- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •Приведённая ниже таблица показывает связь между множествами и случайными событиями.
- •Теория множеств
- •2 Решение типовых задач
- •2) Используем формулу де Моргана
- •Глава 2 Классическое вероятностное пространство.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§3 Задачи для самостоятельного решения
- •§2 Решение типовых задач Задача 1
- •Демонстрационная задача №1
- •Задача 2
- •Демонстрационная задача №2
- •Решение
- •Задача 3
- •Демонстрационная задача №3
- •Решение:
- •Вычисление числовых характеристик.
- •Вычислим вероятности попадания случайных величин в указанные области.
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Приложение
- •Основные свойства функции распределения f(X)
- •Основные непрерывные распределения
Задача 4
Непрерывная случайная величина Х задана функцией плотности:
f(x)=
Найти:1) а; 2)F(x); 3) M[2X-1]; 4) D[5-3X]; 5)найти интервал:
P{X-mx}=1/16
Решение:
1) =1;
=1; dx=1
dx=1
f(x)
2* =1
2a/3*3/4*x4/3
01=1a=2
=1
2a/3*3/4*x4/3
01=1a=2
f(x)=
2/3
1






x
-1


2)
F(x)= ;
;
F(x)=
Замечание:
 +
+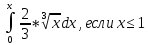
=1/2
если
 то
то -2/3*3/4*х4/3-1х=-1/2*(
-2/3*3/4*х4/3-1х=-1/2*( -1)
-1)
 0х=1/2*
0х=1/2* .
.
Таким образом, функция распределения имеет вид:
F(x)=
Заметим, что, т.к. функция плотности является чётной функцией, т.к.
f(-x)=f(x), то для функции распределения справедлива формулы:
F(-x)=1-F(x); F(0)=1/2 (медиана х=0)
Всегда проверяйте непрерывность функции распределения в точках
«склейки»:
 =0;
=0;
 F(-1)=0
F(-1)=0
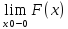 =1/2;
=1/2;
 =F(0)=1/2
=F(0)=1/2
 =F(1)=1;
=F(1)=1;
 =1
=1
F(x)
График
функции распределения:
1
1/2
-1
1






x
3)M[X]=0M[2X-1]=-1
4)D[5-3X]=9*D[X];
D[X]=M[X2]-mx2;
M[X2]=
M[X2]=2* dx=2*3/7*x7/301=6/7
dx=2*3/7*x7/301=6/7
D[X]=6/7
5)P{X-mx}=p0 P{X}=p0P{-X}=p0F()-F(-)=p0
т.к.F(-)=1-F()2*F()-1=p0F()= ;p0=1/16F()=17/32;(>0)
;p0=1/16F()=17/32;(>0)
½+1/2* =17/324/3=1/16=1/8
=17/324/3=1/16=1/8
P{X(-1/8;1/8)}=1/16
Задача5
Непрерывная случайная величина Х задана своей функцией распределения:
F(x)
=

F(x) -Функция распределения
Найти: 1) A, B; 2) f(x); 3) M[2x - 1]; 4) P{[X - mx] < σx} 5) Найти квантили порядка р
а)
р =
 (медиана);
б) р =
(медиана);
б) р = ;
в) р = 9/16
;
в) р = 9/16
Решение:
F(x) – непрерывная функция. Запишем условие непрерывности в точках «склейки»
x
= -2

 ;
;

x
= 2

 =>
12A + B = 1
=>
12A + B = 1
Решаем систему:
 =>
=>

Ax2
+ 4Ax + B =
 x2
+ 4*
x2
+ 4* x
+
x
+ =
= (x+2)
(x+2)
F(x)
=


1
2)f(x) = F`I(x)


3)M[2X - 1] = 2M[X] – 1
 ;
;


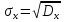
D[X] = M [X2] – mx2
M
[X2]
= ;
;
M
[X2]
=

М[X]
=
 ;
M[X2]
=
;
M[X2]
=

D[X]
= ;
;

P
{|X - mx| < σ}
= P {-0,8 < X < 1,4} = F(1,4) – F(-0,8) =

F(xp) = p -2 ≤ xp ≤ 2

 ;
;
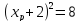 >
>

 ≈ 0,
83
≈ 0,
83
б)
 ;
;
 =>
=>


в)
 ;
;
 =>
=>


Задача 6
По графику функции y = f(x) показать схему графика функции распределения F(x). Заметим, что FI(x) = f(x)
|
f(x) |
F(x) |
|
B(const) |
Bx + C – прямая с угловым k = B |
|
ах+в -прямая |
ax2+bx+с --парабола |
|
ax2+bx+с --парабола |
aх3+вх2+сх+d-кубическая парабола
|
Предполагается, что в схемах графика функции плотности f(x) площадь под графиком равна 1.
--1
1
2
-2-
-1
-1
1
2
3
1













f(x)
-4
x





-3
-2
3









F(x)
x
-4
3-










F(x)
2)
f(x)
1















-3
-1
1
-3
-1
1


x


x

§3 Задачи для самостоятельного решения
Задача 1
Функция
распределения непрерывной случайной
величины задана формулой:
F(x)=
Найти:1)коэффициенты А и В; 2)f(x); 3) M[X]; 4) D[X]; 5)P{X-mxx};
6)квантили порядка «р»: а)р=1/2; b) р=0,2; с)р=0,8;
7)найти интервал: p{X(a;b)}=0,6
Ответ:
1)А=1/4;В=1/2; 2) f(x)= 3)M[X]=0;
4) D[X]=4/3;
5) 1/
3)M[X]=0;
4) D[X]=4/3;
5) 1/ ;
;
6)a)x1/2=0; b)x0,2=-1,2; c)x0,8=1,2; 7) P{X(-1,2;1,2)}=0,6.
Задача 2
Функция распределения непрерывной случайной величины задана
формулой:
F(x)=
Найти:
1) параметр А; 2)f(x);
3) M[X];4)D[2* -3];
5)квантили порядка «р»: а)р=1/2;b)
p=0,1;c)
p=0,7; 6)найти
интервал: P{X(a;b)}=0,4.
-3];
5)квантили порядка «р»: а)р=1/2;b)
p=0,1;c)
p=0,7; 6)найти
интервал: P{X(a;b)}=0,4.
Ответ:
1)А=1/2; 2) f(x)= ;x(1;4);
3)M[X]=
;x(1;4);
3)M[X]= ≈2,16;
≈2,16;
4)D[2* ;
5)a)x1/2=2;
;
5)a)x1/2=2;
b) x0,7=21,4≈2,6;c)x0,1=20,2≈1,15; 6) P{X(1,15; 2)=0,4.
Задача 3
Функция
плотности непрерывной случайной величины
задаётся формулой: f(x)= x[-3;3]
x[-3;3]
Найти: 1)а; 2)F(x); 3)M[4-3*X]; 4)P{X1}; 5)квантили порядка «р»:
а) р=1/2;b) р=1/3; с)р=2/3.
Ответ:1)a=1/3;
2) F(x)= 3) 4;4) 2/3; 5)a)
x1/2=0;
3) 4;4) 2/3; 5)a)
x1/2=0;
b)x1/3=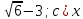 2/3=3-
2/3=3-
Задача 4
Функция распределения непрерывной случайной величины задана
задана
формулой: F(x)=
Найти:1)A;B; 2)f(x); 3)M[X];4) P{X-mxπ/4}
Ответ:1)A=0;B=1;
2)f(x)= 3)
M[X]=1; 4) 0.
3)
M[X]=1; 4) 0.
Задача5
Функция распределения непрерывной случайной величины задана
формулой:F(x)= ;x(0;π/4);
;x(0;π/4);
Найти:1)A;B; 2)f(x); 3)M[3X+2];4) P{X-mxπ/4}
Ответ:1)A=1;B=0;
2)f(x)= 3)M[3X+2]=3*(π/4
-1/2*
3)M[3X+2]=3*(π/4
-1/2*
4)1.
Задача 6
Функция плотности непрерывной случайной величины задаётся
формулой:
f(x)=
Найти: 1)а;2)F(x); 3)M[X-2]; 4)P{X-mxπ/4}.
Ответ:
1)a=1; 2) F(x)=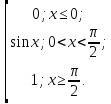 3)π/2
-3; 4)
3)π/2
-3; 4)
 0,97.
0,97.
Задача 7
Функция распределения непрерывной случайной величины задана
формулой:
F(x)=
Найти: 1)A;B; 2) f(x); 3)M[X3+X2+1]; 4)P{X-mx1/4}.
Ответ:1)A=1;
B=0; 2)f(x)=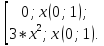 ;3)2,1;
4)7/8.
;3)2,1;
4)7/8.
Задача 8
Функция распределения непрерывной случайной величины задана
формулой:
F(x)=
Найти: 1)A;B; 2)f(x); 3)M[X2+X+1]; 4)P{X-mx2/3}.
Ответ:1)
A=1;B=0; 2)f(x)= ;
3)1
;
3)1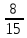 ;
4) 1-
;
4) 1-
Задача 9
Функция распределения непрерывной случайной величины задана
формулой:
F(x)=
Найти: 1)A; 2) f(x); 3)M[4X3+X-5]; 4)P{X1/2}.
Ответ:1)
A=1/2; 2) f(x)= ;
3) -5 ; 4) 5/6.
;
3) -5 ; 4) 5/6.
Задача 10
Функция плотности непрерывной случайной величины задаётся
формулой
:f(x)=
Найти:1)a; 2) F(x); 3) M[4X-5]; 4) квантили порядка «р»:
a)p=1/2; b) p=27/32; c) p=5/32; 5)P{X-mx}=11/16, найти .
Ответ:1)a=3/4;
2) F(x)= 3)-5;
3)-5;
4)a) x1/2=0;b) x27/32=1/2; c) x5/32=-1/2; 5)P{X1/2}=11/16 ( =1/2).
Задача 11
Функция плотности непрерывной случайной величины задаётся
формулой:
f(x)=
Найти:1)a; 2)F(x); 3) M[2X3-4X+7]; 4) P{X-mx}=8/125 ;найти .
Ответ:1)
a=3/4; 2)F(x)= ;
3)7 4)=4/25.
;
3)7 4)=4/25.
Задача 12
Функция плотности непрерывной случайной величины задаётся
формулой:f(x)=
Найти: 1)a; 2)F(x); 3) M[X]; 4)D[X-1]; 5) P{X1}; 6)P{X>0,5}.
Ответ:1)
a=1; 2) F(x)= ;
3) M[X]=1; 4) D[X-1]=1; 5)≈0,37;
6)≈0,785.
;
3) M[X]=1; 4) D[X-1]=1; 5)≈0,37;
6)≈0,785.
Задача 13
В здании областной администрации случайное время ожидания
лифта равномерно распределено в диапазоне от 0 до 5 минут.
Найти:1) функцию распределения F(x).
Чему равна вероятность ожидания лифта более 3,5 минуты?
Чему равна вероятность того, что лифт прибудет в течение первых 45 секунд?
Чему равна вероятность того, что ожидание лифта будет заключено в диапазоне от 1 до 3 минут?
Ответ:1)F(x)= 2)P{3,5X5}=0,3;
3)P{0X3/4}=0,15;
4)P{1X3}=0,4
2)P{3,5X5}=0,3;
3)P{0X3/4}=0,15;
4)P{1X3}=0,4
Задача 14
Мастер, осуществляющий ремонт на дому, может появиться в любое время с 10 до 18 часов. Клиент, прождав до 14 часов , отлучился на 1 час. Какова вероятность, что мастер не застанет его дома?
Ответ:P{14X15}=0,25.
Задача 15
Владелец антикварного аукциона полагает, что предложение цены за определенную картину будет равномерно распределённой случайной величиной в интервале от 500 тыс. рублей до 2 млн.рублей.Найти:
Дифференциальную функцию.
Определите вероятность того, что картина будет продана за цену. меньшую чем 675 тыс. рублей.
Найдите вероятность того, что цена картины будет выше 2 млн. рублей.
Ответ:а)
f(x)= b)P{X675}=0,1167;
c)
P{X>2}=0.
b)P{X675}=0,1167;
c)
P{X>2}=0.
Задача 16
На перекрёстке дорог движение регулируется автоматически светофорам, включающим зелёный свет через каждые 2 минуты. Время простоя у этого светофора автомобиля. оставшегося на красный свет, есть случайная величина , распределённая равномерно на интервале (0;2) минут.
Найдите среднее время простоя и среднее квадратическое отклонение.
Ответ:M[X]=1; x≈0,5773.
Задача 17
Измеряется температура термометром с ценой деления в 10.Отсчёт производится с точностью до одного градуса.
Величина ошибки измерения Х есть случайная величина , распределённая равномерно в диапазоне (-0.50; +0.50).
Найдите среднюю ошибку измерения , а также стандартное отклонение.
Ответ: M[X]=0; x=0,2887.
Задача 18
Срок службы жёсткого диска компьютера – случайная величина, подчиняющаяся показательному закону со средней в 12000 часов.
Найдите долю жёстких дисков, срок службы которых превысит 20000 часов.
Ответ:P{X>20000}=1-F(20000)= ≈0,188
(a=
≈0,188
(a= )
)
Задача 19
Срок службы батареек для слуховых аппаратов подчиняется показательному закону с параметром а=1/2.
Какова доля батареек со сроком службы больше чем 9 дней?
Ответ:
P{X>9}=1-F(9)= ≈0,47237.
≈0,47237.
Задача 20
Служащий рекламного агентства утверждает, что время, в течении которого телезрители помнят содержание коммерческого рекламного ролика, подчиняется экспоненциальному закону с параметром а=0,25 дня. Найдите долю зрителей, способных вспомнить рекламу через неделю.
Ответ:P{X>7}=1-F(7)= ≈0,17377
≈0,17377
Задача 21
Компьютерный программист использует показательное распределение для оценки надёжности своих программ. После того , как он нашёл 10 ошибок. он убедился. что время (в днях) до нахождения следующей ошибки подчиняется показательному закону с параметром а=0,25.
Найдите среднее время, потраченное для нахождения первой ошибки, . и определите вероятность того, что для нахождения первой ошибки понадобится более 5 дней, а также вероятность того, что на нахождение одиннадцатой ошибки потребуется от 3 до 10 дней.
Ответ:M[X]=1/а =4 (дня)- среднее время, потраченное на нахождение первой ошибки4*10=40 (дней)
M[X]=40
a=1/40=0,025; P{X>5}= =
= ≈0,8825;
≈0,8825;
P{3X10}=F(10)-F(3)=0,92775-0,7788=0,148955.
