§2 Решение типовых задач

Задача 1

f(x)=;

Найти:

1) а, построить график f(x)

2) F(x) и построить график

3) M[χ]

4) D[χ]

5) Проверить, что число х=1 является квантилью порядка p=20/27

6) Найти интервал [a;b]: P{χϵ(a,b)}=13/27

Решение

1) Основное свойство функции плотности:

f(x)dx=1. В нашем случае a(9-x²)dx=1

[Заметим, что f(x)dx=0, если f(-x)=f(-x) (нечетная)

f(x)dx=2 f(x)dx, если f(-x)=f(x) (четная)]

2а (9-x²)dx=1=>2a(9x-x³/3) =1

2a(27-9)=1=> a=1/36

f(x)= 1/36(9-x²), xϵ[-3;3]

0, xȼ[-3;3]

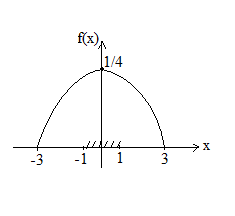
F(x)= f(x)dx 0, x<-3

F(x)= 1/36 (9-x²)dx, xϵ[-3;3]

1, x>3

1/36 (9-x²)dx=1/36(9x-x³/3) =1/36(9x-x³/3+27-9)≈1/36(9x-x³/3+18)

F(x)=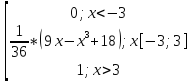 функция распределения:

контроль:F(-3)=0; F(0)=0,5; F(3)=1

Заметим, что f(-x)=f(x)=> F(-x)=1-F(x)

Медиана M_e=0, т.к F(x)=1/2 ,при x=0

3) M[χ]=o, т.к. x∙(9-x²)dx=0 (нечетная функция)

D[χ]=M[χ²]-m²x

M[χ²]= x²(9-x²)dx=2 (9x²-x⁴)dx=2(9x³/3-x⁵/5) =2(81-243/5)=64,8

D[χ]=64,8

5) Число χ_p называется квантилью порядка р, если F(x_p)=p или P{χ<x_p}=p

F(1)=20/27 Это означает, что число 1 есть квантиль порядка p=20/27

1=x_20/21

Заметим, что квантиль порядка p=7/27-это число -1,т.к. F(-1)=1-F(1)=1-20/27=7/27

6) P{χϵ(a,b)}=13/27=F(b)-F(a)

Пусть b=x_20/27=1; a=x_7/27=-1

F(b)=20/27; F(a)=7/27

Ответ: P{X[-1;1]}=13/27

Задача 2

f(x)= Найти:

1)а; 2)F(x); 3)M[X]; 4)D[X]; 5)квантили порядка р :а)р=1/2 (медиана);

в)р=1/9;с)р=16/25; д)найти интервал (а;в): P{X-m_x}=4/9

Решение:

1)Основное свойство функции плотности:

=1 площадь под графиком равна 1

=11/2*a*3=1a=2/3

f(x)

a

x

-1

2

f(x)=

2)F(x)= 

F(x)=

=2/9_-1^x=1/9(x+1)²

; -1≤x≤2;

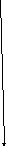
F(x)

1

1/2

1/9

Me

-1

x

2

3) M[X]=M[X]=2/9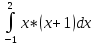

=2/9(x³/3 +x²/2 )_-1²=2/9*(8/3+2+1/3-1/2)=1

M[X]=1

4)D[X]=M[X²]-m_x²; M[X²]=  M[X²]=2/9=

2/9=2/9*(x⁴/4-x³/3)_-1² =2/9*(4-8/3-1/4+1/3)=17/12

D[X]=17/12-1=5/12

5) х_р- квантиль порядка «р»;заметим, что -1≤х_р≤2

По определению: F(x_p)=p1/9*(x_p+1)²=p

a)p=1/21/9*(x_p+1)²=1/2 (x_p+1)²=9/2 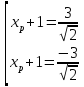

Me=≈1,14.

о.д.з.

b)p=1/91/9*(x_p+1)²=1/9  x_p+1=11/9*(x_p+1)²=16/25

 x_p+1=12/5 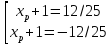



х_16/25=1,2

d) P{X-m_x}=p₀P{m-Xm+}=p₀F(m+)-F(m-)=p₀

1/9*(1++1)²-1/9*(1-+1)²=p_0p₀=4/9 1/9(2+)²-1/9(2-)²=4/9

(2+)²-(2-)²=4(2+-2+)*(2++2-)=4=1/2

P{X-11/2}=4/9P{1/2X3/2}=4/9

Задача 3

f(x)=x>1.

Найти:1)а; 2)F(x); 3)M[X]; 4)D[X]; 5)P{X2};6)P{x3} ; 7)P{X-m}

Решение:

1)Основное свойство функции плотности:

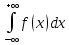=1 =1

-a/2*₁^+∞=-a/2(-1)=a/2a/2=1a=2

f(x)

f(x)=

1

x

2

2) F(x)=

F(x)=; x>1 =2*(-1/2)*₁^x=-+1

F(x)=

11

1

F(x)

1

x

1

3) M[X]=M[X]==

Формула интегрирования по частям: =u*v-

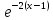=-x*₁^+∞+=(-x*-1/2)₁^+∞=

=(x+1/2)₁^∞=-+1+1/2=1,5M[X]=1,5

Примечание:=[]=[]=0

правило Лопиталя

4) D[X]=M[X²]-m_x²; M[X²]=M[X²]==

=-x²₁^∞+=-+1+1,5=2,5

M[X]=1,5

по правилу

Лопиталя =0

D[X]=2,5-(1,5)²=0,25D[X]=0,25_x=_x=0,5

5)P{X2}=F(2)=1-e^-2≈0,73

6) P{x3}=1-P{X3}=1-(F(3)-F(-3))1-1+e^-4≈0,0183

=0

; 7)P{X-m}=P{m-Xm+}=P{1X2}=F(2)-F(1)=1-e^-2≈0,73

=0