Задача2
Процент людей, купивших новое средство от головной боли после того, как увидели его рекламу по телевидению, есть случайная величина Х . заданная рядом распределения :
|
Х |
0 |
10 |
20 |
30 |
40 |
50 |
|
p |
0,10 |
0.20 |
0,35 |
.0.20 |
0,10 |
0,05 |
Убедитесь, что действительно задан ряд распределения.
Найдите функцию распределения F(x) и постройте её график.
Определите вероятность того, что более 20 % людей откликнутся на рекламу
Найдите среднее число людей купивших новое средство.
Ответы:
а)
=1
;с)P{X>2}=0,35;d)
M[X]=21,5;
е)P[X-mxx}=0,75.
Задача 3
В лотерее на 100 билетов разыгрываются две вещи, стоимости которых 210 и 60 условных денежных единиц
Составить закон распределения суммы выигрыша для лица ,имеющего:а) один билет, б) два билета.
Стоимость билета -3 условных единицы.
Убедитесь в справедливости свойства о математическом ожидании
суммы случайных величин.
Ответ:
а)Х- сумма выигрыша на один билет
|
Х |
Не выиграл -3 |
Выиграл первую вещь 57 |
Выиграл вторую вещь 207 |
|
Р |
0,98 |
0,01 |
0,01 |
б)X+Y-сумма выигрыша на два билета.
|
X+Y |
-6 |
54 |
204 |
264 |
|
Р |
4753/4950 (0,9602) |
49/2475 (0,0198) |
49/2475 (0.0198) |
1/4950 (0.0198) |
Задача 4
Журнал «Деньги» в одном из номеров поместил информацию о том, что возврат инвестиций Х на российском рынке в 1990 году ожидался более высоким , чем от аналогичных инвестиций на американском рынке. Консультант по инвестициям , советующий вкладывать средства в российский рынок, полагает., что вероятностное распределение возврата инвестиций (% в году) в один из таких проектов имеет вид:
|
Х |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Р |
0,05 |
0.15 |
0,30 |
0,20 |
0,15 |
0,10 |
0,05 |
Убедитесь, что задан ряд распределения.
Чему равна вероятность того, что возврат инвестиций будет составлять по крайней мере 12%?
Найдите функцию распределения F(х) и постройте её график.
Среднее число возврата инвестиций.
Если Y=3-2*Х , то найдите дисперсию D[Y].
Ответы
а)
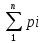=1
;b)
P{X12}=0,5,d)M[X]=11.75;
e)D[Y]=42.71
Задача 5
Распределение станочного парка на заводе по числу аварий задано следующей функцией распределения:
F(х)=
.
Найти: а) ряд распределения; в)M[X]; с)х
Ответ:
в) M[X]=44/85;
с)х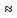
0,92
Задача 6
В урне содержится два чёрных и один красный шар. Из этой урны дважды извлекают шар, а затем снова возвращают в урну.
Пусть Х- число извлечённых чёрных шаров.
Построить ряд распределения.
Полигон распределения.
Функцию распределения F(х).
Математическое ожиданиеM[X].
Дисперсию D[X].
Ответ:а)
|
Х |
0 |
1 |
2 |
|
Р |
1/9 |
4/9 |
4/9 |
d)M[X]=4/3; e)D[X]=4/9.
.
Задача 7
При подбрасывании двух игральных костей игрок А выигрывает 2 рубля., если сумма открывшихся очков равна 2 или 3, и выигрывает 4 рубля, если эта сумма равна 4.Во всех остальных случаях он проигрывает 1 рубль.
Найдите математическое ожидание выигрыша для игрока А.
Выгодна ли для игрока А эта игра?
Ответ:
Х-выигрыш игрока А при каждом бросании двух костей.
|
Х |
2 |
4 |
-1 |
-1 |
… |
-1 |
|
Р |
1/36+2/36=3/36 |
3/36 |
Р1 |
Р2 |
… |
рк |
р1+р2+..+рк=1-3/36-3/36=5/56.
M[X]=-1/3.
Вывод: Игра для игрока А НЕ ВЫГОДНА!