Задача 13.

Однотипные приборы выпускаются тремя заводами в количественном отношении ;;, причём вероятность брака для этих заводов соответственно равны,. Прибор, приобретённый научно – исследовательским институтом, оказался бракованным.

Какова вероятность того, что данный прибор произведён первым заводом?

Ответ:

p () =+

p () =+

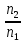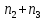
p () =+

Задача 14.

Предположим, что надёжность определения туберкулёза при рентгене составляет 90% (т.е. 10% носителей туберкулёза остаются неопознанными). Вероятность того, что у здорового человека будет ошибочно определён туберкулёз, составляет 1%. Просвечиванию была подвергнута большая группа людей со средним процентом больных, равным 0,1%.

Какова вероятность того, что человек, признанный больным действительно является носителем туберкулёза?

Ответ: 0,0826

примечание:

= {носители туберкулёза} P () = 0,001

= {здоровый человек} P () = 0,994

A = {человек признан больным}

= 0,9; 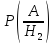= 0,01.

Найти

Глава 6 Последовательность независимых испытаний

по схеме Бернулли.

§1.Основные понятия

Пусть проводится «n» независимых испытаний ( опытов).

В каждом опыте возможны только два исхода: А (успех ) или 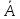( неудача).

Независимо от номера опыта Р(А)=р; Р=q=1-р.

Вероятность появления события А в серии из «n» опытов ровно

«к» раз вычисляется по формуле Бернулли:

Р_n(к)= С_n^k*p^k*q^n-k, (к=0, 1, 2, …, n).

Заметим, что вероятности Р_n(к) называются биномиальными

и при этом справедливы формулы:

1. Р_n(0)+ P_n(1) +…+P_n(n)=1.

2. Вероятность того, что А появится хотя бы один раз:

P_n(1) +…+P_n(n)=1- qⁿ.

3.Вероятность того, что А появится не менее «m» раз:

P_n(m)+ P_n(m+1)+…+P_n(n)=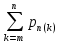=1-

4.Вероятность того, что А появится не более «m» раз:

Р_n(0)+ P_n(1) +…+P_n(m)=(k) =1-(k).

Число К₀ при котором биномиальная вероятность наибольшая,

называется наивероятнейшим числом появления А в «n» испытаниях

и может быть определено из неравенства:

n*p – q ≤k₀≤n*p+p.

При этом, если n*p –целое, то к₀=n*p;

если n*p-q=k₁ ( целое) n*p+p= k₂ (целое), то P_n(k₁)=P_n(k₂)

и тогда будем иметь два наивероятнейших числа.

Примечание:

Если « n» велико, а « р"достаточно мало, то можно использовать

приближённую формулу Пуассона для вычисления биномиальных

вероятностей:

P_n(k)^k/k!)*e^-, где =n*p

В дальнейшем будут рассмотрены ещё другие формулы для приближённых вычислений биномиальных вероятностей.

Все биномиальные вероятности можно представить в виде

таблицы ( биномиальное распределение).

Биномиальное распределение

Х –число появлений события А в «n» независимых испытаниях Бернулли

P{X=k}= P_n(к)=C_n^kp^k*q^n-k, к=0,1,…,n

X	0	1	2	…	k	…	n
P	qn	nqn-1p	Cn2 qn-2 p2	…	Cnkpkqn-k	…	pn

§2 Решение типовых задач

Задача 1

Элементы цепи работают независимо друг от друга.

А_i={«i» элемент исправен}, i=1, 2, 3, 4.

2

1

3

4

Пусть Р(А₁)=0,3; Р(А₂)=0,4; Р(А₃)=0,7; Р(А₄)==0,6.

Цепь включали пять раз.

Найти вероятности следующих событий:

1. B={ не менее двух раз был отказ цепи}

2. C={цепь работала ровно два раза}

3. Наивероятнейшее число отказов.

4. Сколько раз нужно включить цепь. чтобы она работала с вероятностью не менее 0.9 хотя бы один раз?

Решение:

Сначала найдём вероятность работы цепи при одном включении:

А=А₁*(А₂+А₃*А₄); (события совместные, но независимые в совокупности).

Р(А)= Р(А₁)*(Р(А₂)+Р(А₃)*Р(А₄)-Р(А₂)*Р(А₃)*Р(А₄))

Р(А)=0,3*(0,4+0,7*0.6-0,4*0,7*,6)=0,1956.

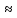Р(А)0,2; Р()0,8.

Схема Бернулли

n=5 (число испытаний)

Пусть 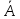(отказ) интересующее нас событие.

р= Р()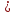0,8;q=0,2.

1. Р(В)=Р₅(2)+Р₅(3)+Р₅(4)+Р₅(5)=1.

2)С={цепь работала ровно два раза}{ровно три был отказ}

Р₅(3)=С₅³*р³*q²=10*0,8³*0.2²=0,2048

Р(С)=0.2048

3)К₀-наивероятнейшее число отказов.

n*p – q ≤k₀≤n*p+p.

3,8≤к₀≤4,8,к₀=4

4. Сколько раз нужно включить цепь. чтобы она работала с вероятностью не менее 0.9 хотя бы один раз?

1-Рⁿ0,90,8ⁿ≤0,1 n-1/10,3n11.

Задача 2

В результате многолетних наблюдений для некоторой местности было установлено, что вероятность выпадения дождя 13 июля равна 4/17. Найти наивероятнейшее число дождливых дней 13 июля в ближайшие 50 лет.

Решение:

А={выпадение дождя 13 июля}; Р(А)=р=4/17;q=13/17; n=50

n*p – q ≤k₀≤n*p+p.

50*4/17-13/17≤к₀≤50*4/17+4/17 11≤к₀≤12

Ответ: или 11 или 12.

Задача 3

Пара одинаковых игральных костей бросается 7раз.

Какова вероятность следующих событий:

1. А={ сумма очков, равная 7.,выпадет дважды}

2. B={ сумма очков, равная 7, выпадет по крайней мере один раз}

3. C={каждый раз выпадет сумма очков больше 7}

4. D={ни разу не выпадет сумма очков, равная 12}

Решение:

Опыт (число испытаний ) :бросают две игральных кости.

Число всех исходов опыта :n(Ω)=6²=36

Обозначим А₁={сумма очков равна 7}

Возможны варианты:

2+5=7	3+4=7	1+6=7
5+2=7	4+3=7	6+1=7

Число исходов события А₁: n(А₁)=6

Тогда: Р(А₁)=n(A₁)/n(Ω)=6/36=1/6/

Cхема Бернулли для 1) и 2) n=7; р(А₁)=р=1/6;, q=5/6.

1)Р(А)=С₇²*р²*q⁵=(7*6/2)*(1/6)²*(5/6)⁵=0,2344

2)Р(В)=1-q⁷=1-(5/7)⁷=0,721.

Пусть А₂={сумма очков больше 7}

Возможны варианты:

	3+5=8	3+6=9	4+4=8		5+5=10		6+6=12
6+2=8	5+3=8	6+3=9	4+5=9		5+6=11
				5+4=9		6+5=11
				4+6=10
				6+4=10

Число исходов события А₂: n(А₂)=15  Р(А₂)=15/36.

Схема Бернулли для 3)

n=7; р(А₂)=р=15/36; q=21/36.

Задача 4

Два равносильных шахматиста договорились сыграть матч из 2n результативных партий. Ничьи не учитываются и считается , что каждый из участников может выиграть очередную партию с вероятностью 0,5.Выигравшим матч считается тот, кто победит в большем числе партий.

В каком матче больше шансов выиграть любому из участников:

в матче из 8 результативных партий или из 12?

Решение:

n=8 n=12

А{выигрыш} А{выигрыш}

р(А)=0,5; q=0,5 р(А)=0,5; q=0,5

Найти: Р₅(8) Найти: Р₁₂(7)

(пять партий дают (семь партий дают выигрыш

выигрыш в этом матче) в этом матче).

Решение Решение

Р₅(8)=С₈⁵*р⁵* q³=56*(0,5)⁸ Р₁₂(7)=С₁₂⁷*р⁷*q⁵=792*(0.5)¹²

0.21875 0,193

Вывод: Р₅(8)> Р₁₂(7) Более вероятно выиграть в матче из 8

Задача 5

Партию телевизоров разделили на две группы:

8 и 10 телевизоров соответственно в каждой

Вероятность брака для каждого телевизора первой группы равна 0,5, а второй 0,4.

Какое из двух событий более вероятно:

B={в первой группе не более двух бракованных}

C={во второй группе не менее трёх годных}

Решение:

Первая группа	Вторая группа
А={бракованный телевизор} Р(А)=р=0.5; q=0,5	А={годный телевизор} Р(А)=0,6 ; q=0,4
Найти: Р8(2)+Р8(3)+…+Р8(8)= 1- Р8(0)- Р8(1)=Р(В)	Найти:Р10(3)+Р10(4)+…+Р10(10)= 1-Р10(0)-Р10(1)-Р10(2)=Р(С)
Решение: Р8(0)=q8=(0,5)8 Р8(1)=С81*р*q=8*(0,5)8	Решение: Р10(0)=(0,4)10=0,000104857 Р10(1)=С101*р*q9=10*(0.4)9*0,6= 0,00157 Р102=С102*р2*q8=45*(0,6)2(0,4)8=0,0106
Р(В)=1-9*(0,5)8=0,9648	Р(С)0,988

Ответ: Вероятнее событие С

Задача 6

В аптеке проводят ревизию особо дорогостоящего лекарства.

Вероятность брака одной упаковки лекарства равна 0,1.

Сколько нужно проверить упаковок лекарств, чтобы с вероятностью не менее 0,99, обнаружить хотя бы одно бракованное?

Решение:

Дано: А={бракованное лекарство} ;Р(А)=р=0,1;q=0,9

В={хотя бы одно бракованное}

Найти: «n»

Р(В)=1-qⁿ0,99 qⁿ≤0.010,9ⁿ≤0.01n*≤-2n-2/43,7

Ответ: не менее 44

Задача 7

По трём каналам связи передаётся сообщение .

Вероятность искажения сообщения для каждого канала равна 0,1.

Сообщение будет принято с вероятностью 1, если оно

прошло по всем трём каналам; с вероятностью 0,7, если оно прошло по двум каналам и с вероятностью 0,4, если оно прошло по одному каналу.

Найти вероятность события А: А={сообщение принято полностью}.

Решение:

Для решения задачи используем формулу полной вероятности:

Гипотезы Hi	P(Hi)	P(A/Hi)	P(Hi)*P(A/Hi)
H1={прошло по трём каналам}	P(H1)=0.93=0.729	1	0,729
Н2={прошло по двум каналам}	Р(Н2)=С32*0,92*0,1= 0,243	0,7	0.243*0,7= 0,1701
H3={прошло по одному каналу}	Р(Н3)=С31*0,9*0,12= 0,027	0,4	0,027*0,4=0,0108
∑			Р(А)=0,9099

По формуле полной вероятности:

Р(А)=Р(Н₁)*Р(А/Н₁)+Р(Н₂)*Р(А/Н₂)+Р(Н₃)*Р(А/Н₃)

Ответ:0,9