
- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •Приведённая ниже таблица показывает связь между множествами и случайными событиями.
- •Теория множеств
- •2 Решение типовых задач
- •2) Используем формулу де Моргана
- •Глава 2 Классическое вероятностное пространство.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§3 Задачи для самостоятельного решения
- •§2 Решение типовых задач Задача 1
- •Демонстрационная задача №1
- •Задача 2
- •Демонстрационная задача №2
- •Решение
- •Задача 3
- •Демонстрационная задача №3
- •Решение:
- •Вычисление числовых характеристик.
- •Вычислим вероятности попадания случайных величин в указанные области.
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Приложение
- •Основные свойства функции распределения f(X)
- •Основные непрерывные распределения
Глава 5. Формула полной вероятности. Формулы Байеса.
§1. Основные понятия
Пусть H1, H2,…,Hn – наблюдаемые события для данного эксперимента, при чем они попарно несовместны (Hi*Hj=ᴓ) и образуют полную группу событий (H1+H2+…+Hn= Ω).
Для
любого наблюдаемого в эксперименте
события A имеет место следующая
формула полной вероятности: 
События H1, H2,…, Hn принято называть гипотезами. Безусловные вероятности P(Hi), где i =1,.. ,n трактуются как доопытные (априорные) вероятности гипотез.
Замечание: Формулу полной вероятности используют в условиях неопределенности, т.е. когда неизвестно, какая из гипотез Hi реализовалась.
Если событие
A реализовалось, то послеопытные
(апостериорные) вероятности гипотез
определяются по формулам
Байеса: P( )
=
)
= ,
i=
,
i=
 ;
;
 = 1
= 1
Формулы Байеса позволяют «переоценить» вероятность каждой из гипотез после поступления «живой» информации относительно осуществления тех или иных наблюдаемых событий.
§2. Решение типовых задач. Задача 1
Издательство разослало рекламные материалы на новый учебник по бухгалтерскому учету, которые получили 80% профессоров, читающих этот курс в различных ВУЗах. Отобрали и приняли эту книгу для преподавания 30% профессоров, получивших рекламные материалы и 10% не получивших. Найти вероятности следующих событий:
Случайно выбранный профессор ВУЗа принял этот учебник для преподавания.
Профессор, принявший учебник для преподавания, получил рекламные проспекты.
Решение:
A={случайный профессор одобрил и принял учебник к преподаванию}
|
H1={профессор получил рекламные материалы} |
0,8 |
0,3 |
0,8×0,3 = 0,24 |
|
Гипотезы Hi |
P(Hi ) |
|
P(Hi
)× |
|
H2={профессор не получил рекламные материалы} |
0,2 |
0,1 |
0,2×0,1 = 0,02 |
|
∑ |
1 |
- |
P(A) = 0,26 |
P(A)=P(H1)×P( )+P(H2)×P(
)+P(H2)×P(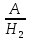 )=0,24+0,02=0,26
P(
)=0,24+0,02=0,26
P( )
=
)
=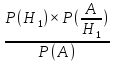 =
=
 =
0,9231
=
0,9231
Задача 2
Для участия в студенческих отборочных спортивных соревнованиях из первой группы выделено 4 студента, из второй – 6, из третьей - 5 студентов. Вероятности попадания для студентов каждой группы в сборную университета соответственно равны 0,5; 0,4 и 0,3.
Какова вероятность того, что случайно выбранный участник соревнований попал в сборную?
Случайно выбранный участник соревнований попал в сборную. К какой из этих групп он вероятнее всего принадлежи
Решение:
A={случайно выбранный участник соревнований попал в сборную}
1)
|
Гипотезы Hi |
P(Hi ) |
|
P(Hi )× |
|
H1={студент первой группы} |
|
0,5 |
|
|
H2={студент второй группы} |
|
0,4 |
|
|
H3={студент третьей группы} |
|
0,3 |
|
|
∑ |
1 |
- |
P(A)= |
P(A)=P(H1)×P( )+P(H2)×P(
)+P(H2)×P( )
+ P(H3)
× P(
)
+ P(H3)
× P( )
=
)
=
 =0,393
2)
P(
=0,393
2)
P( )
=
)
= =
=
 =
=

P(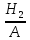 )
=
)
= =
=
 =
=
P( )
=
)
= =
=
 =
=
Ответ: вероятнее всего участник будет из второй группы.
Задача 3
Из ящика, содержащего 9 пар обуви, из которых 2 пары мужской, 2 пары женской и 5 пар детской (обувь в одинаковых коробках), перекладывается 1 пара обуви в другой ящик, содержащий 1 пару мужской, 4 пары женской и 2 пары детской обуви. Из второго ящика случайным образом берут одну пару обуви.
Какова вероятность, что это детская обувь?
2 Какова вероятность, что из первого ящика во второй переложили пару детской обуви?
Решение:
A={случайно выбранная обувь из второго ящика - детская}
1)
|
Гипотезы Hi |
P(Hi ) |
|
P(Hi )× |
|
H1={из первого ящика во второй переложили мужскую обувь} |
|
|
|
|
H2={ из первого ящика во второй переложили женскую обувь } |
|
|
|
|
H3={ из первого ящика во второй переложили детскую обувь } |
|
|
|
|
∑ |
1 |
- |
P(A)=
|
P(A)=P(H1)×P( )+P(H2)×P(
)+P(H2)×P( )
+ P(H3)
× P(
)
+ P(H3)
× P(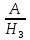 )
=
)
=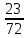 2)P(
2)P( )
=
)
=
 =
=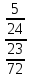 =
=

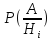
 )
)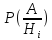

 ×
0,5=
×
0,5=


 ×0,4=
×0,4=


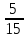 ×
0,3=
×
0,3=





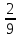 ×
× =
=

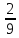
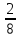
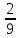 ×
× =
=



 ×
× =
=

