Задача №6

Вероятность того, что потребитель увидит рекламу определённого продукта по телевидению, равна 0,04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0,06. Предполагается, что оба события независимы. Найти вероятности событий:

1. А = {потребитель увидит обе рекламы}

2. В = {потребитель увидит хотя бы одну рекламу}

Решение:

А₁ = {реклама на телевидении}

A₂ = {реклама на стенде}

Р (А₁) = 0,04; P(A₂) = 0,06

Найти : 1) Р(А) 2) Р(В)

Решение:

1. А = А₁ × А₂ т.к независимы, то Р (А) = Р (А₁) × Р (А₂)

Р (А) = 0,04 × 0,06 = 0,024

2. В = А + В

Р (В) = Р (А₁) + Р (А₂) – Р (А₁×А₂) или Р (В) = 1 – Р (A₁) × Р(A₂)

Р (В) = 1 - 0,96 × 0,94 = 0,0976

Задача 7.

Вероятность того, что Маша и Юля купят обе одинаковый костюм, равна 0,4. Вероятность того, что Маша купит, а Юля не купит, равна 0,5.

Найти вероятность того, что Маша костюм не купит.

Дано: А={Маша купила костюм}

В={Юля купила костюм}

р(А*В)=0,4

Найти: р(Ā)-?

Решение:

=> р(А)=0,4+0,5=0,9

р(Ā)=0,1

Ответ: 0,1.

Задача 8.

В магазине происходит сезонная распродажа товаров. Вероятность того, что будет продана коллекция верхней одежды, равна 0,7, коллекция обуви – 0,8, а парфюмерии – 0,6. Найти вероятности событий:

1) А={все продали}

2) В={продали только один вид товара}

3) С={обувь продали и хотя бы один из оставшихся видов товаров тоже продали}

4) В={хотя бы один вид товара продали полностью}

Дано:

А₁={продали коллекцию верхней одежды} р(А₁)=0,7 р(Ā₁)=0,3

А₂={продали коллекцию обуви} р(А₂)=0,8 р(Ā₂)=0,2

А₃={продали коллекцию парфюмерии} р(А₃)=0,6 р(Ā₃)=0,4

Заметим, что события А₁, А₂, А₃ совместные, но независимые в совокупности.

Найти:

1) р(А); 2) р(В); 3)р(С); р(D)

Решение:

1. А= А₁*А₂*А₃ , т. к. события независимы в совокупности, то

по теореме умножения:

р(А)=р(А₁)*р(А₂)*р(А₃)=0,8*0,7*0,6=0,336

2)

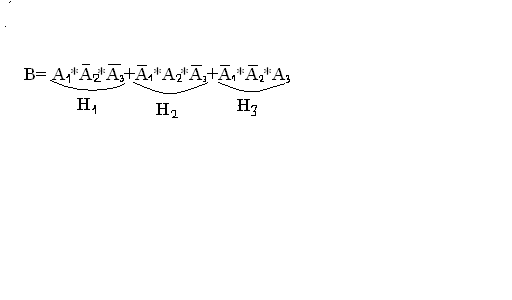
В=Н₁+Н₂+Н₃ События Н₁, Н₂, Н₃ попарно несовместны.

Н_i *H_j =ø (i≠j)

р(В)=р(Н₁)+р(Н₂)+р(Н₃)

р(Н₁)=р(А₁)*р(Ā₂)*р(Ā₃)=0,7*0,2*0,4=0,056

р(Н₂)=р(Ā₁)*р(А₂)*р(Ā₃)=0,3*0,8*0,4=0,096

р(Н₃)=р(Ā₁)*р(Ā₂)*р(А₃)=0,3*0,2*0,6=0,036

р(В)=0,056+0,096+0,036=1,188

3)С=А₃ *(А₁+А₂)

Р(С)=р(А₃)*р(А₁+А₂)=р(А₃)*(1-р(Ā₁)*р(Ā₂))=0,6*(1-0,3*0,2)=0,564

4)D=A₁+A₂+A₃

P(D)=1-р(Ā₁)*р(Ā₂)*р(Ā₃)=1-0,3*0,2*0,4=0,976

Ответ: 1) 0,336; 2) 0,188; 3)0,564; 4)0,976.

Задача 9.

Рассчитать работу электрической цепи

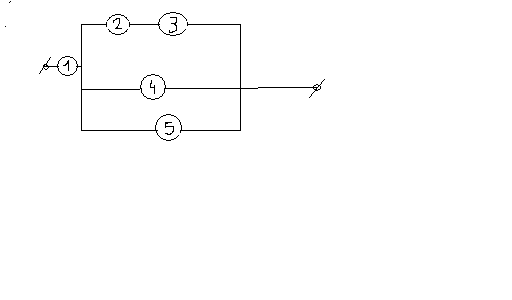
А_i ={“i” элемент исправен}

р(А₁)=р(А₅)=0,6; р(А₂)=р(А₄)=0,7;

р(А₃)=р(А₆)=0,4

А={цепь исправна}

[события А_i совместные, но независимые в совокупности]

Решение:

А=А₁*А₆*(А₂*А₃+А₄+А₅)

р(А)=р(А₁)*р(А₆)*р(А₂*А₃+А₄+А₅)

р(А₂*А₃+А₄+А₅)=1-*р(Ā₄)*(Ā₅)

=1-(А₂*А₃)=1-р(А₂)*р(А₃)=1-0,7*0,4=0,72

р(А)=0,6*0,4*(1-0,72*0,3*0,4)=0,219264

Задача 10.

Дано: р(Ā*В)=0,3

р(В)=0,2

Найти: 1) ; 2); 3) р(В+С)

Решение:

Заметим, что:

Р(В+С)=1-0,4=0,6

Ответ: 1) 0,7; 2) 0,6; 3) 0,6.

Задача 11.

Дано: р(В)=0,6; р(Ā*В)=0,2; р(Ā+В)=0,7.

Найти: 1) р(А); 2)р(А*В); 3) р(А+В).

Решение:

1. р(Ā+В)=р(Ā)+р(В)-р(Ā*В)

0,7=р(Ā)+0,6-0,2 => р(Ā)=0,3

Р(А)=0,7

2) Ā*В+А*В=В р(В)=р(Ā*В)+р(А*В)

0,6=0,2+р(А*В) => р(А*В)=0,4

3) р(А+В)=р(А)+р(В)-р(А*В)=0,7+0,6-0,4=0,9

Ответ: 1) 0,7; 2) 0,4; 3) 0,9.