
Л 1-4. Произведение векторов
1. Разложение вектора на компоненты.
Р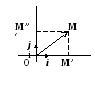 ассмотрим
вектор
ассмотрим
вектор
![]() ,
заданный своими координатами:
,
заданный своими координатами:
![]() .
.
![]()
![]()
![]()
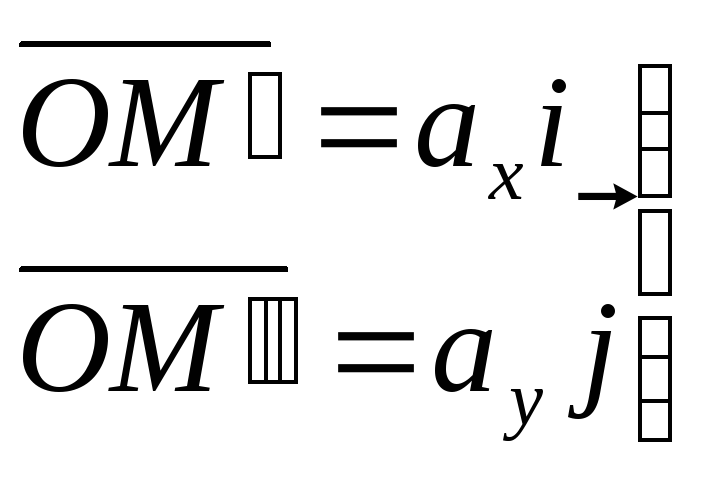 -
компоненты вектора
-
компоненты вектора
![]() по направлениям базисных векторов
по направлениям базисных векторов
![]()
![]() .
.
Выражение вида
![]() называется разложением вектора
называется разложением вектора
![]() на компоненты.
на компоненты.
Аналогичным образом можно разложить
на компоненты вектор
![]() :
:
![]() .
.
Косинусы углов, образованные рассматриваемым
вектором
![]() с базисными ортами
с базисными ортами
![]() называются направляющими косинусами
называются направляющими косинусами
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
2. Скалярное произведение векторов.
Скалярным произведением двух векторов
![]() и
и
![]() называется число, равное произведению
модулей этих векторов на косинус угла
между ними
называется число, равное произведению
модулей этих векторов на косинус угла
между ними
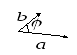
![]()
Скалярное произведение двух векторов
можно рассматривать как произведение
модуля одного из этих векторов на
ортогональную проекцию другого вектора
на направление первого
![]() .
.
Свойства:
-
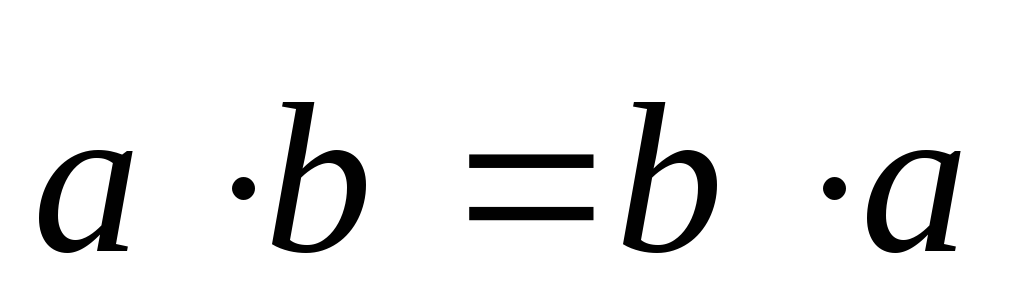 ;
; -
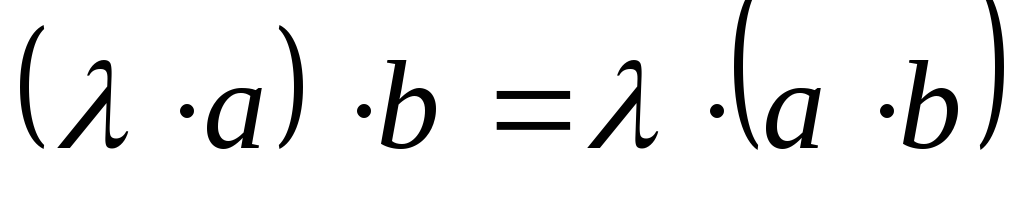 ;
; -
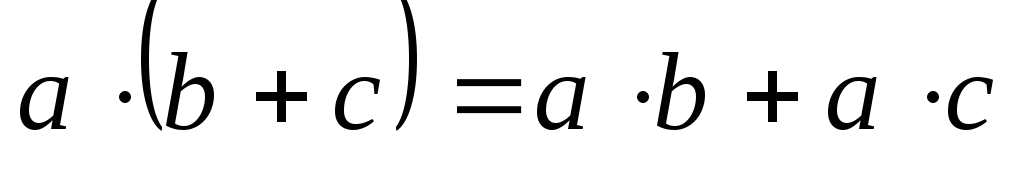 ;
; -
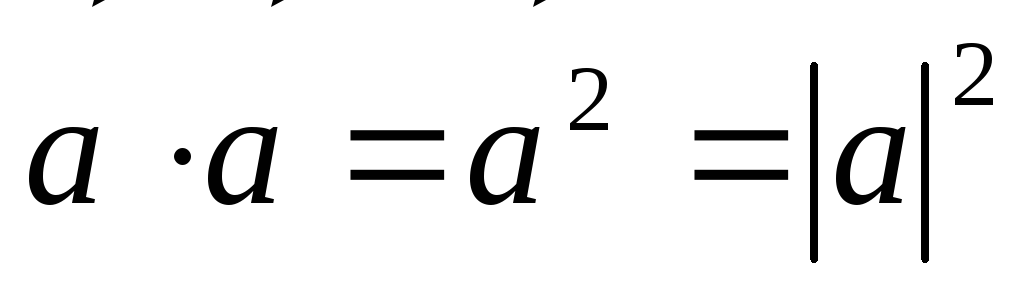 - скалярный квадрат вектора;
- скалярный квадрат вектора; -
если
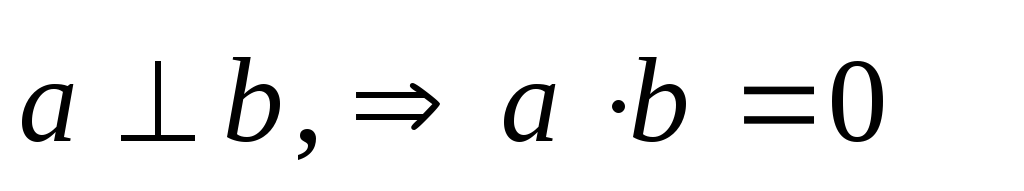
Если известны координаты векторов
![]() и
и
![]() ,
то, выполнив разложение векторов на
компоненты
,
то, выполнив разложение векторов на
компоненты
![]() и
и
![]() ,
найдём
,
найдём
![]()
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() ,
то
,
то
![]() .
.
![]() .
.
Условие перпендикулярности векторов:
![]() .
.
Условие коллинеарности ректоров:
![]() .
.
3. Векторное произведение векторов.
![]()
Векторным произведением вектором
![]() на вектор
на вектор
![]() называется такой вектор
называется такой вектор
![]() ,
который удовлетворяет условиям:
,
который удовлетворяет условиям:
-
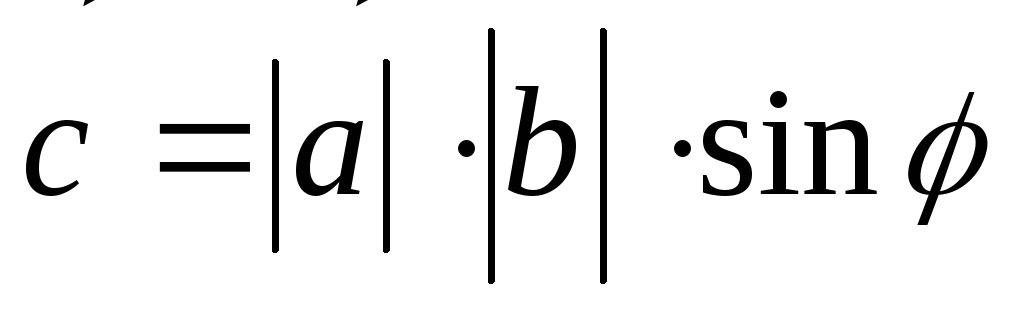 ;
; -
вектор
 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов
 и
и
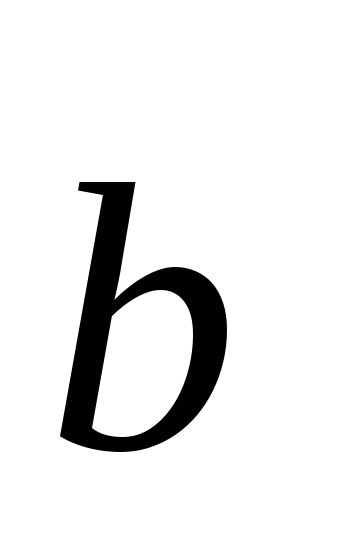 ,
т.е.
,
т.е.
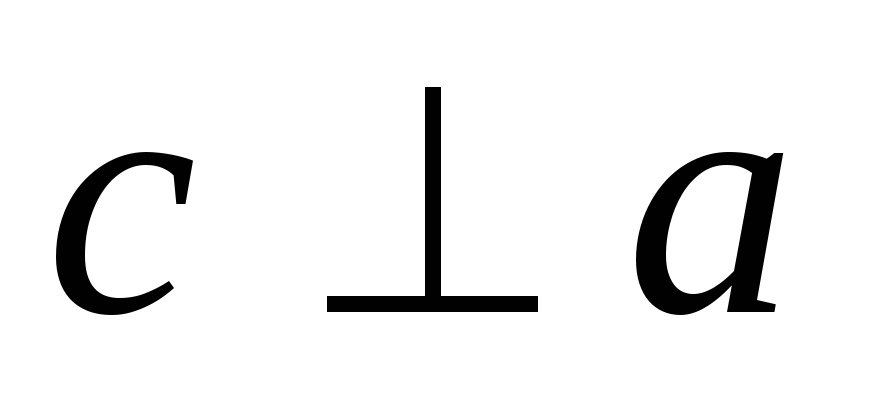 ,
,
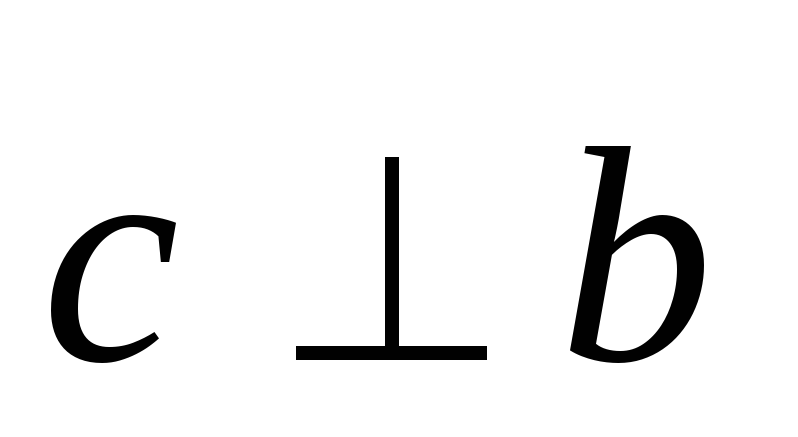 ;
; -
вектор
 направлен так, что если смотреть с конца
вектора
направлен так, что если смотреть с конца
вектора
 ,
то кратчайший поворот вектора
,
то кратчайший поворот вектора
 к вектору
к вектору
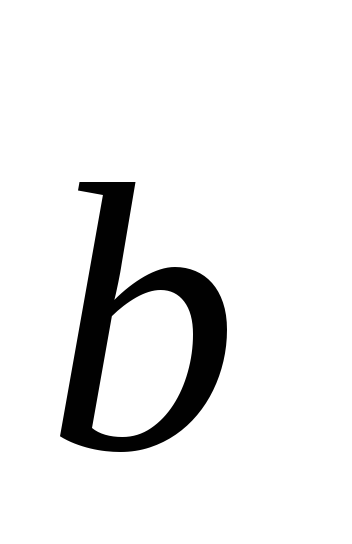 должен происходить против часовой
стрелки.
должен происходить против часовой
стрелки.
Свойства:
-
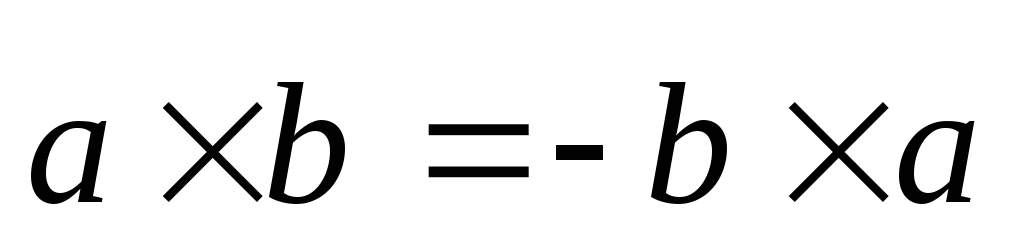 - действие векторного произведения
анти коммутативно;
- действие векторного произведения
анти коммутативно; -
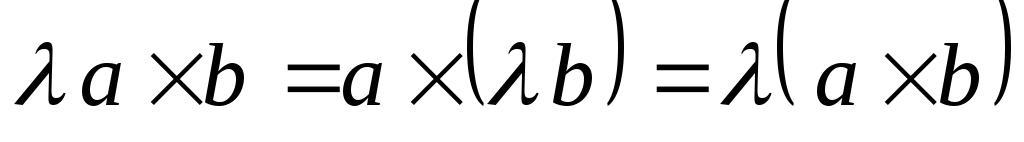 - ассоциативно относительно на число;
- ассоциативно относительно на число; -
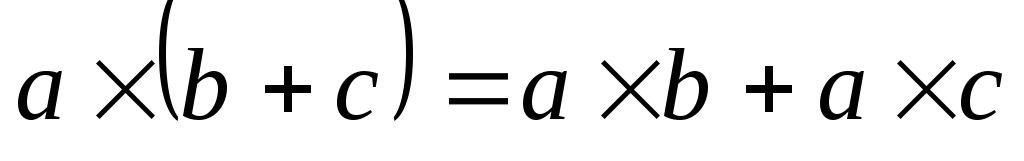 - дистрибутивно относительно сложения
векторов;
- дистрибутивно относительно сложения
векторов; -
Если векторы
 и
и
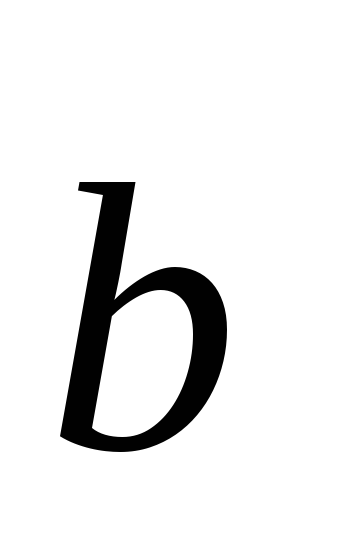 коллинеарны, то
коллинеарны, то
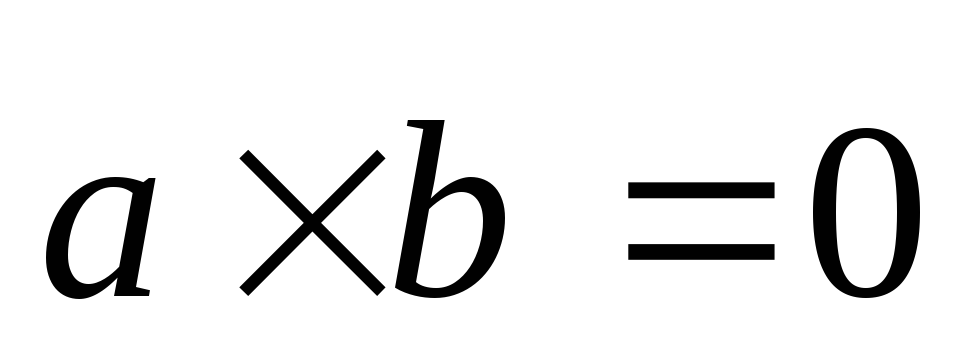 ,
в частности
,
в частности
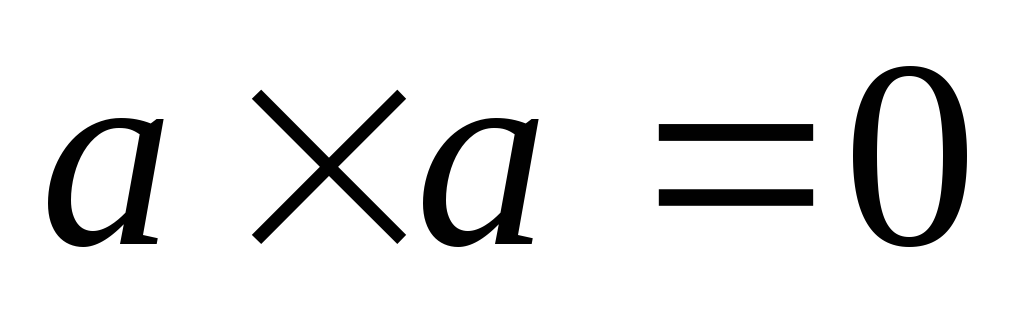 .
.
Рассмотренные алгебраические свойства позволяют найти аналитическое выражение для векторного произведения через координаты составляющих векторов в ортонормированном базисе.
Дано:
![]() и
и
![]() .
.
![]()
![]()
![]()
т.к.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]()
![]()
![]()
![]()
![]() .
Эту формулу можно записать короче, в
форме определителя третьего порядка:
.
Эту формулу можно записать короче, в
форме определителя третьего порядка:
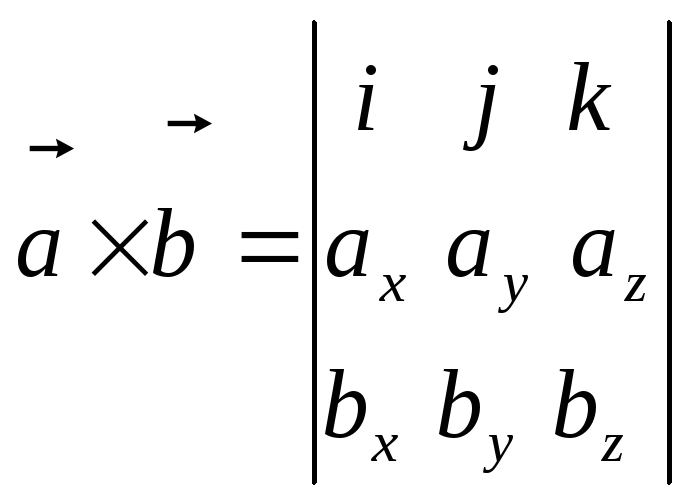 .
.
4. Смешанное произведение векторов.
Смешанным произведением трех векторов
![]() ,
,
![]() и
и
![]() называется число, равное векторному
произведению
называется число, равное векторному
произведению
![]() ,
умноженному скалярно на вектор
,
умноженному скалярно на вектор
![]()
.
Верно следующее равенство:
![]() ,
поэтому смешанное произведение записывают
,
поэтому смешанное произведение записывают
![]() .
.
Как следует из определения, результатом смешанного произведения трёх векторов является число. Это число имеет наглядный геометрический смысл:
Модуль смешанного произведения
![]() равен объёму параллелепипеда, построенного
на приведённых к общему началу векторах
равен объёму параллелепипеда, построенного
на приведённых к общему началу векторах
![]() ,
,
![]() и
и
![]() .
.
Свойства смешанного произведения:
-
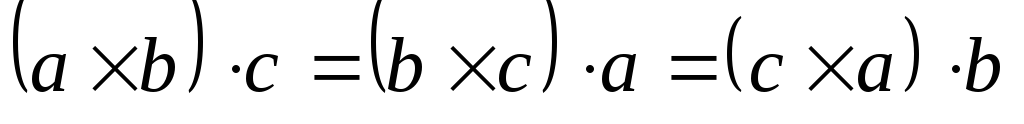 ,
т. е. смешанное произведение не меняется
при циклической перестановке векторов;
,
т. е. смешанное произведение не меняется
при циклической перестановке векторов; -
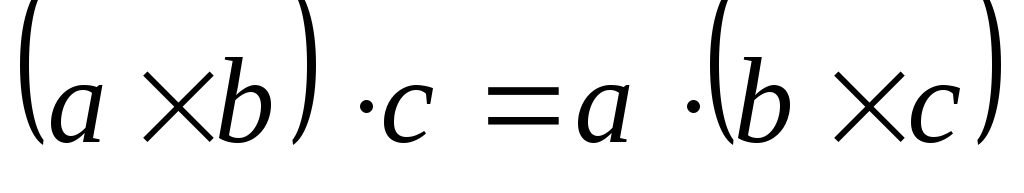 т. е. смешанное произведение не меняется
при перестановке знаков векторного и
скалярного произведения;
т. е. смешанное произведение не меняется
при перестановке знаков векторного и
скалярного произведения; -
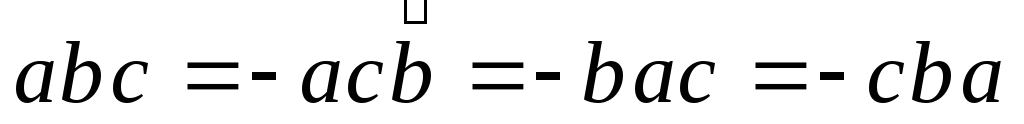 ,
т.е. смешанное произведение меняет знак
на противоположный при перестановки
двух векторов – сомножителей;
,
т.е. смешанное произведение меняет знак
на противоположный при перестановки
двух векторов – сомножителей; -
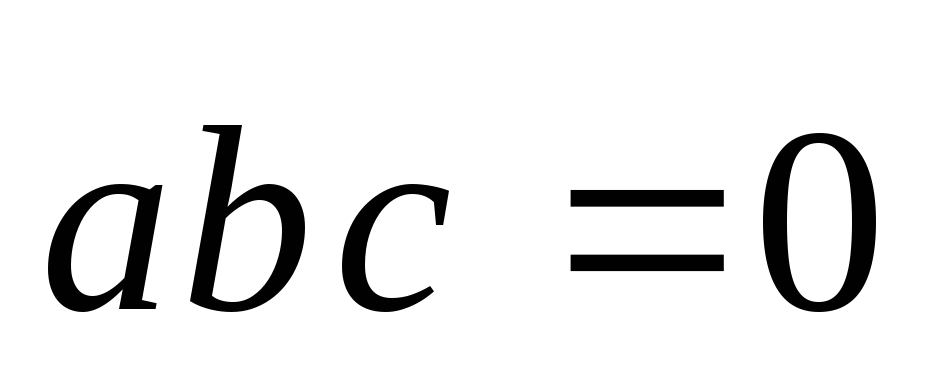 (объём параллелепипеда равен нулю),
если векторы
(объём параллелепипеда равен нулю),
если векторы
 ,
,
 ,
,
 лежат в одной или параллельных плоскостях,
следовательно они компланарны или два
из перемножаемых векторов коллинеарны.
лежат в одной или параллельных плоскостях,
следовательно они компланарны или два
из перемножаемых векторов коллинеарны. -
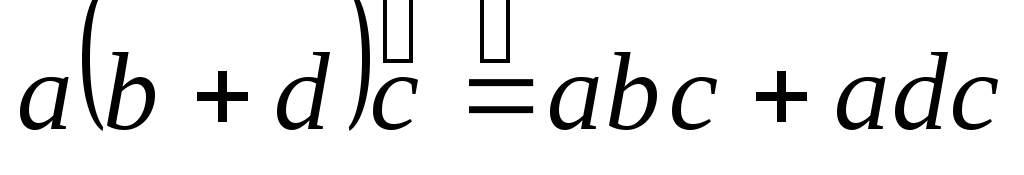 ;
; -
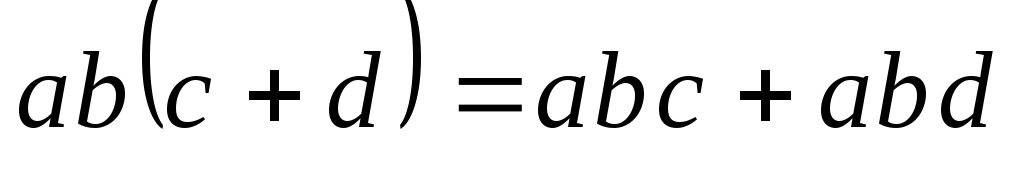 ;
; -
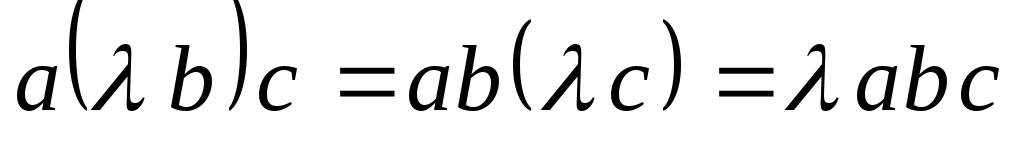 .
.
Если векторы
![]() ,
,
![]() ,
,
![]() заданы в ортонормированном базисе
заданы в ортонормированном базисе
![]() своими координатами, вычисление
смешанного произведения осуществляется
по формуле
своими координатами, вычисление
смешанного произведения осуществляется
по формуле
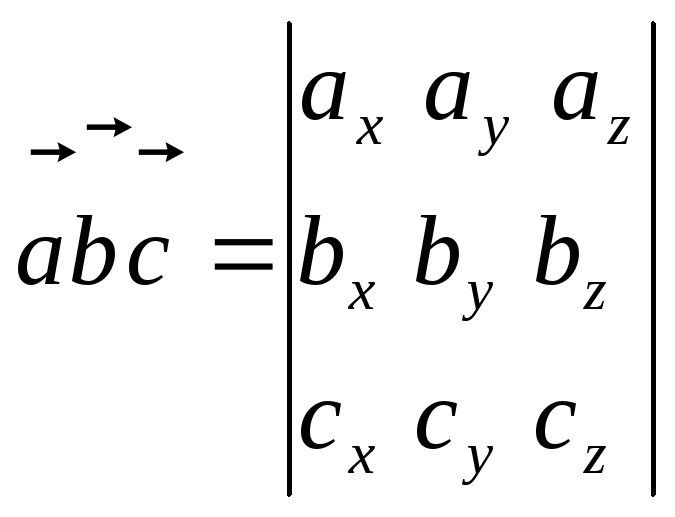 .
.
Действительно, если
![]() ,
то
,
то
![]()
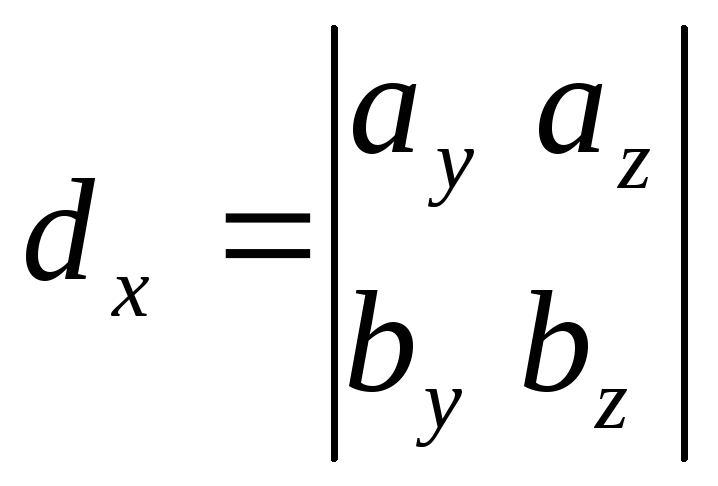 ;
;
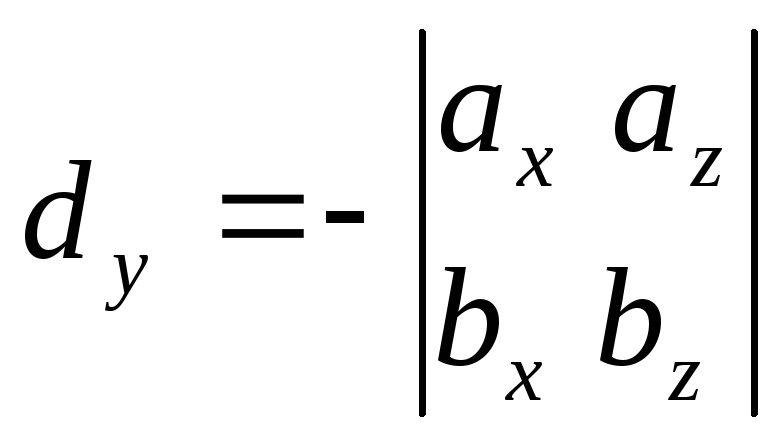 ;
;
![]() ,
тогда
,
тогда
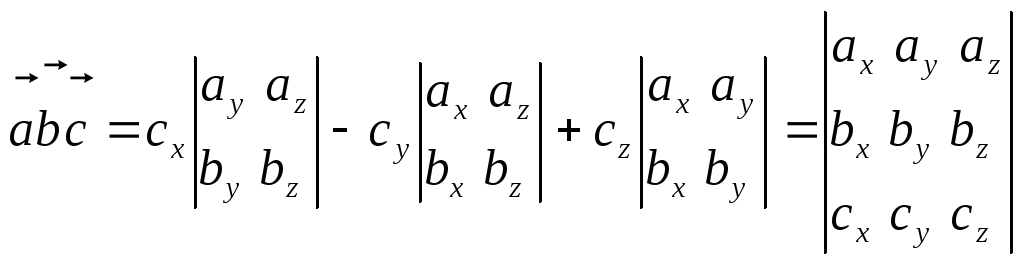 .
.
Если векторы
![]() ,
,
![]() ,
,
![]() компланарны, то векторное произведение
компланарны, то векторное произведение
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
И наоборот, если
.
И наоборот, если
![]() ,
то объем параллелепипеда равен нулю, а
это возможно только в том случае, когда
векторы компланарны (линейно зависимы).
,
то объем параллелепипеда равен нулю, а
это возможно только в том случае, когда
векторы компланарны (линейно зависимы).
Таким образом, три вектора компланарны, тогда и только тогда, когда их смешанное произведение равно нулю.
