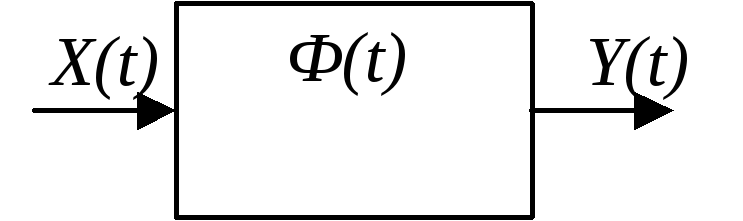2.5. Типовые воздействия

Схемная функция (рис. 2.14) представляет собой аналитическое выражение Ф(t), описывающее связь входного X(t) и выходного Y(t) сигналов электрической (электронной) цепи через ее параметры. Схемная функция является математической моделью схемы.
	Рис. 2.14

Так как реальные входные и выходные сигналы могут быть достаточно сложными функциями времени, то для экспериментальных и теоретических исследований электрических цепей и электронных устройств в качестве входных сигналов используют сигналы специальной вида, называемые типовыми воздействиями. Тип используемого воздействия определяет и тип используемой схемной функции.

Обычно используются три вида типовых воздействий.

1. Гармоническое с единичной амплитудой, графическое представление которого и аналитическое описание приведено на рис. 2.15.

	В общем случае . В данном случае , поскольку , где - угловая частота и - циклическая частота. В комплексной форме .
Рис. 2.15

2. Ступенчатое с единичной амплитудой (единичная функция, импульс включения, единичный скачок, функция Хевисайда), графическое представление которого и аналитическое описание приведено на рис. 2.16.

	. Площадь сигнала .
без запаздывания
	. Площадь сигнала .
с запаздыванием
Рис. 2.16

3. Импульсное (единичный импульс, дельта-функция, единичная импульсная функция, функция Дирака), графическое представление которого и аналитическое описание приведено на рис. 2.17.

	. Длительность импульса амплитуда импульса . Площадь импульса .
без запаздывания
	. Длительность импульса амплитуда импульса . Площадь импульса .
с запаздыванием
Рис. 2.17

2.6. Комплексный коэффициент передачи. Частотные характеристики цепи

Каждому типу входных воздействий соответствует своя схемная функция. Их названия, обозначения и характеристики приведены в табл. 2.5.

Таблица 2.5
Название	Обозначение	Характеристика
Передаточная функция		Коэффициент передачи по току , по напряжению или по мощности
Комплексный коэффициент передачи		Комплексный коэффициент передачи или амплитудно-фазочастотная характеристика (АФЧХ) схемы
Переходная характеристика		Переходная характеристика
Весовая функция		Весовая функция или импульсная переходная характеристика

При гармоническом входном воздействии в качестве схемной функции используется комплексный коэффициент передачи , представляющий собой отношение комплексной переменной (выходной сигнал) к комплексной переменной (входной сигнал) : . Поскольку - комплексная переменная, которая на комплексной плоскости изображается вектором, то при изменении от до конец вектора описывает кривую.

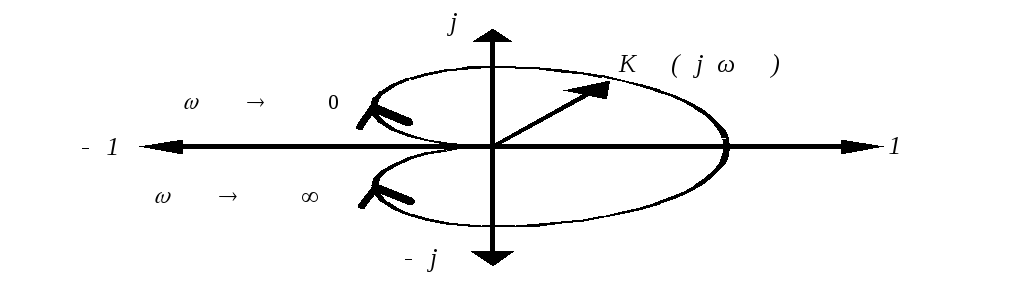
Эта кривая называется амплитудно-фазочастотной характеристикой или годографом на комплексной плоскости. Для примера на рис. 2.18 изображен годограф для усилителя низкой частоты. Комплексный коэффициент передачи можно представить следующим образом ,
	Рис. 2.18

где - модуль АФЧХ, представляющий собой амплитудно-частотную характеристику (АЧХ), а- аргумент , представляющий собой фазочастотную характеристику (ФЧХ).

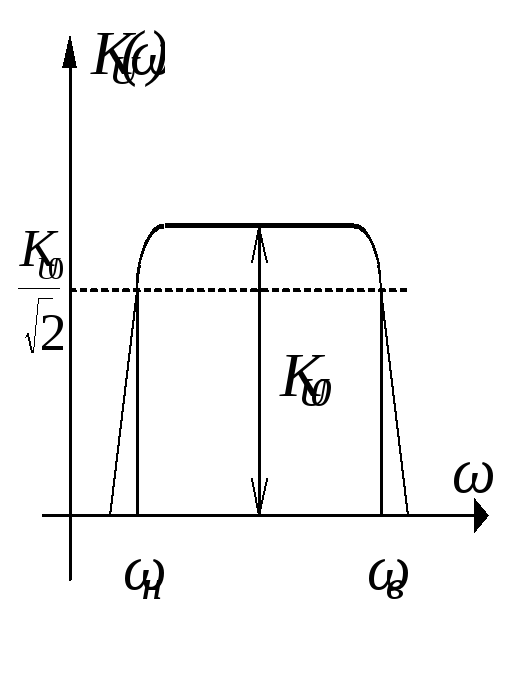
Годографы используют чаще всего при оценке устойчивости, а также для специальных устройств, а именно, для генераторов гармонических колебаний. В большинстве случаев рассматривают АЧХ схемы и ФЧХ схемы. Например, для упомянутого ранее усилителя низкой частоты АЧХ изображена на рис. 2.19, а ФЧХ – на рис. 2.20.

Рис. 2.19	Рис. 2.20

На АЧХ (рис. 2.19) имеется участок в диапазоне частот, где модуль комплексного коэффициента передачи не меняется () или меняется незначительно. Диапазон частот, в которомизменяется не более чем в заданное число раз, называется рабочим диапазоном частот. В приведенном примере задано возможное уменьшениедо значения враз меньшего, чемв середине рабочего диапазона частот, и определены граничные частоты в области нижнихи верхнихчастот. При этом средняя частота, для которой определяется, связана с граничными частотами выражением. На ФЧХ (рис. 2.20) в рабочем диапазоне частот нулевой фазовый сдвиг, а за его пределами – ненулевой.