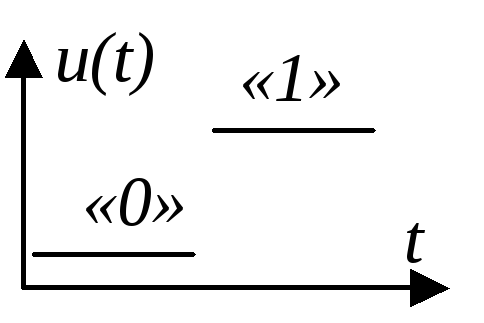2.2. Электрические сигналы и их классификация

В соответствии с принятой традицией сигналом называют процесс изменения во времени физического состояния какого-либо объекта, служащий для отображения, регистрации и передачи сообщений. На практике сообщения неразрывно связаны с заключенной в них информацией. Круг вопросов, базирующихся на понятиях «сообщение» и «информация», является объектом изучения в дисциплине «Теория информации» и выходит за рамки дисциплины «Электротехника и электроника». Поэтому далее не будет излагаться связь, которая существует меду физическим обликом сигнала и смыслом заключенного в нем сообщения.

Для того, чтобы сделать сигналы объектами теоретического изучения и расчетов, следует указать способ их математического описания или, другими словами, создать математическую модель сигнала. Математической моделью сигнала может быть, например, функциональная зависимость, аргументом которой является время. Математические модели электрических сигналов, рассматриваемых в электротехнике и электронике, обычно обозначаются символами латинского алфавита ,и т.д. Зная математические модели сигналов, можно сравнивать эти сигналы между собой, устанавливать их тождество и различие, проводить классификацию.

Классифицируя сигналы по виду моделирующей их функции времени, можно выделить аналоговые и дискретные сигналы (табл.2.1).

Если сигнал имеет математическую модель вида непрерывной или кусочно-непрерывной функции, то он называется аналоговым.

Если значения сигнала определены не во все моменты времени, а лишь в счетном множестве точек, то такой сигнал называется дискретным.

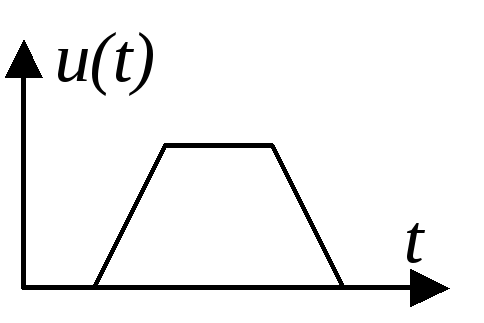
Дискретные сигналы в свою очередь подразделяются на импульсные и цифровые. Если сигнал в виде изменения тока или напряжения существует лишь в пределах конечного интервала времени, то такой сигнал называется импульсным. Особой разновидностью дискретных сигналов являются цифровые сигналы. Для них характерно то, что отсчетные значения сопоставлены числам. По соображениям удобств технической реализации и обработки обычно используется двоичная система счисления.

Таблица 2.1. Типы сигналов
Аналоговые
непрерывные		кусочно-непрерывные
Дискретные
импульсные		цифровые
		положительная логика	отрицательная логика

Аналоговые сигналы обрабатываются аналоговыми устройствами, которые работают в линейном режиме, то есть не меняют свою функцию во всем рабочем диапазоне входного сигнала. С дискретными сигналами работают элементы и устройства, в которых используются как линейный, так и нелинейный режим работы активных элементов.

Для математического описания аналоговых устройств и сигналов, а также устройств импульсной техники и импульсных сигналов используются классические и операторные методы математики и электротехники. Устройства и элементы цифровой техники описываются с помощью алгебры логики.

Аналоговые и импульсные сигналы могут быть модулированными и немодулированными.

При модуляции используется определенный физический процесс, называемый переносчиком или несущей. Математической моделью переносчика может служить функция времени Z(t,A,B,…), зависящая также от параметров А, В,….

Некоторые параметры функции фиксированы, и тогда они могут играть роль идентифицирующих параметров, т.е. по ним можно определять принадлежность данного сигнала к определенному классу сигналов.

Другие параметры подвергаются воздействию, называемому модуляцией, а эти параметры играют роль информативных параметров.

В общем случае модуляция есть отображение множества возможных значений входного сигнала на множество значений информативного параметра переносчика. Устройство, осуществляющее модуляцию, называется модулятором. Устройство, осуществляющее обратное преобразование, называется демодулятором.

На один вход модулятора (рис. 2.3) действует реализация входного сигнала X(t), на другой – сигнал-переносчик Z(t,A).
	Рис. 2.3

Модулятор формирует выходной сигнал Y(t,A[X(t)]), информативный параметр которого изменяется во времени в соответствии с передаваемым сигналом.

Основное назначение модуляции состоит в перенесении спектра сигнала в заданную частотную область.

В зависимости от вида используемого при модуляции переносчика различают непрерывные (аналоговые) и импульсные виды модуляции.

При непрерывной модуляции в качестве несущего используется гармоническое колебание.

Пусть, например, Z(t)= U_msin(t+ ). В качестве информативных параметров могут быть использованы амплитуда U_m, частота , фаза . Название модуляции определяется по тому, какой параметр колебания используется в качестве информативного (табл. 2.2).

Таблица 2.2. Виды непрерывной модуляции
Несущая	Z(t)= Usin(t+ )
Информативный параметр	Um
Вид модулированного сигнала
Название вида модуляции	амплитудная	частотная	фазовая

При импульсных видах модуляции в качестве несущей используется периодическая последовательность прямоугольных импульсов. Если при импульсной модуляции изменяется амплитуда импульсов, то это амплитудно-импульсная модуляция (АИМ), длительность импульса – широтно-импульсная модуляция (ШИМ), период следования импульсов – время-импульсная модуляция (ВИМ).

Применяются также комбинированные виды модуляции, когда используются несколько информативных параметров несущей. Существуют комбинированные методы модуляции как для непрерывной, так и для импульсной модуляции. Примеры: АЧМ – амплитудно-частотная модуляция, АШИМ – амплитудно-широтно-импульсная модуляция.

Модуляция – это процесс нелинейный, ее результат также является нелинейным. Например, если , а, тогда при амплитудной модуляции

,

где - коэффициент амплитудной модуляции, определяющий глубину модуляции. Таким образом, для получениявыполняется операция перемножения, являющаяся нелинейной, поэтому и схема, ее реализующая (модулятор), является нелинейным устройством.

Следовательно, схемы модулятора и демодулятора – нелинейные устройства. В схемах модулятора и демодулятора применяются нелинейные активные и пассивные элементы (диоды, транзисторы), которые работают как в линейном, так и в нелинейном (ключевом) режиме.

Выбор той или иной формы представления информации называется кодированием в широком смысле. Обратный процесс выявления информации, представленной в сигнале, называется декодированием в широком смысле. Под кодированием в узком смысле понимаются преобразования дискретных форм представления информации. Таким образом, кодирование в широком смысле включает в себя и модуляцию, и кодирование в узком смысле.