Резистивный элемент

Существуют линейные (рис. 1.33), нелинейные (рис. 1.34) и параметрические (рис. 1.35) резистивные элементы.

Главный параметр резистивного элемента – сопротивление электрическому току, поэтому часто используется второе название резистивного элемента - сопротивление. Единицей измерения сопротивления является Ом. Величина, обратная сопротивлению , называется проводимостью и измеряется в Сим. Мгновенная мощность. Энергия. Поскольку энергия всегда положительна, то резистивный элемент только потребляет ее и является пассивным элементом.

Условно-графическое обозначение	Условно-графическое обозначение
		Пример—диод
Математическая модель: - закон Ома для резистивного элемента	Математическая модель диода:
Графическое представление математической модели – вольтамперная характеристика (ВАХ)	Графическое представление математической модели – ВАХ диода
Рис. 1.33	Рис. 1.34

Условно-графическое обозначение

Рис. 1.35

Индуктивный элемент

Индуктивный элемент – элемент, в котором энергия электрического поля преобразуется в энергию магнитного поля. При протекании тока через индуктивный элемент возникает потокосцепление. Индуктивный элемент предназначен для накопления электромагнитной энергии. Как и резистивный элемент, индуктивный элемент может быть линейным (рис. 1.36), нелинейным (рис. 1.37) и параметрическим (рис. 1.38).

Условно-графическое обозначение	Условно-графическое обозначение
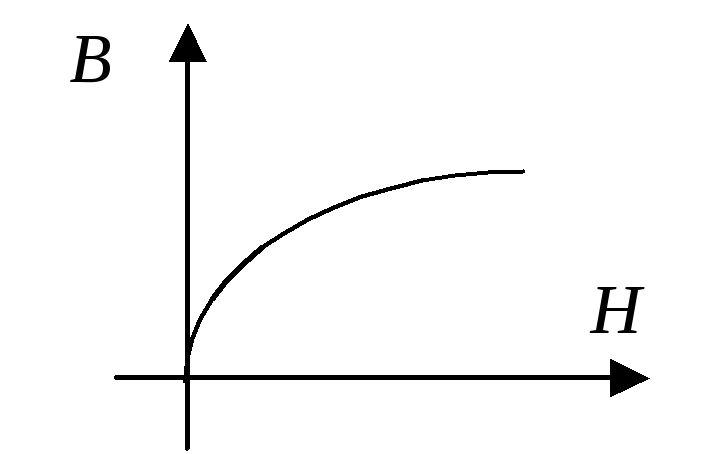
Математическая модель: - устанавливает связь потокосцепленияс вызвавшим его током,- коэффициент пропорциональности, называемый индуктивностью;, где- магнитный поток, обусловленный только токами цепи,- число витков, с которыми сцеплен поток	Математическая модель: зависимость магнитной индукции от напряженностимагнитного поля
Графическое представление математической модели – вебер-амперная характеристика	Графическое представление математической модели
Рис. 1.36	Рис. 1.37

Условно-графическое обозначение

Рис. 1.38

Математическая модель линейного индуктивного элемента устанавливает связь между i_L и u_L в индуктивном элементе: - ЭДС самоиндукции, возникающая на зажимах индуктивного элемента при протекании тока через него. Напряжение на зажимах индуктивного элемента равно. По главному параметруиндуктивный элемент имеет упрощенное название – индуктивность.

Мгновенная мощность , которая может быть как больше нуля в процессе намагничивания, так и меньше нуля в процессе размагничивания. Энергия, т.е. индуктивный элемент является пассивным, как и резистивный элемент.

Пример реального индуктивного элемента – дроссель с сердечником или катушка индуктивности (рис. 1.39). При протекании тока через катушку индуктивности возникает ЭДС самоиндукции, препятствующая изменению тока в ней, в связи с чем в выражении появляется знак «минус».
	Рис. 1.39

Ёмкостный элемент

Ёмкостный элемент предназначен для накопления энергии в электрическом поле, поскольку преобразует напряжение в заряд на обкладках конденсатора. Как и резистивный элемент, емкостный элемент может быть линейным (рис. 1.40), нелинейным (рис. 1.41) и параметрическим (рис. 1.42).

Условно-графическое обозначение	Условно-графическое обозначение
		Пример—варикап
Математическая модель: - устанавливает связь заряда, накопленного емкостью, с напряжениемна ней. Главный параметр – емкость	Графическое представление математической модели – кулон-вольтная характеристика
Графическое представление математической модели – кулон-вольтная характеристика	Характеристика варикапа
Рис. 1.40	Рис. 1.41

Условно-графическое обозначение

Рис. 1.42

Математическая модель устанавливает связь между мгновенными значениями тока и напряжения. Поскольку , то. Мощностьможет быть больше нуля при заряде емкости и меньше нуля при ее разряде.

Энергия . Поскольку во всех случаяхW>0, то все емкостные элементы являются пассивными.

Источники ЭДС и тока.

Условно-графическое обозначение и вольтамперные характеристики идеального источника ЭДС и идеального источника тока приведены на рис. 1.43 и рис. 1.44 соответственно.

Условно-графическое обозначение	Условно-графическое обозначение
Rвн=0	Gвн=0
Вольтамперная характеристика	Вольтамперная характеристика
Рис. 1.43	Рис. 1.44

Идеализированные источники тока и напряжения имеют внешнюю характеристику (рис. 1.45), описываемую прямой линией , что позволяет получить математическую модель реального (идеализированного) источника.

Рис. 1.45

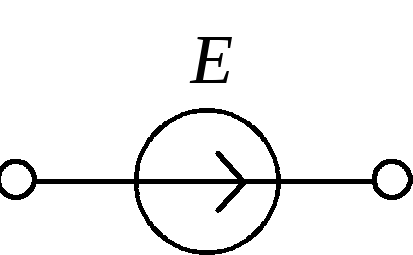
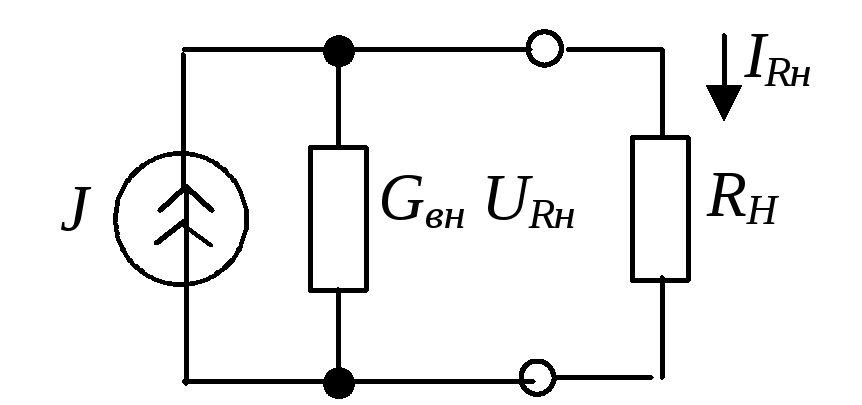
Математическая модель идеализированного источника ЭДС представлена на рис. 1.46, а идеализированного источника тока - на рис. 1.47.

Рис. 1.46

Рис. 1.47

Таким образом, идеальные источники ЭДС и тока друг в друга эквивалентно не преобразуются. Идеализированные источники ЭДС и тока преобразуются друг в друга в соответствии с выражением E = ЈR_вн и рис. 1.48

Рис. 1.48

Выбор того или иного описания (источник ЭДС или источник тока) зависит от соотношения R_н и R_вн. Если R_н > R_вн, то лучше использовать схему с источником ЭДС. Если наоборот, то удобнее использовать эквивалент с источником тока.