3.4.2. Операторный метод анализа переходных процессов

Классический метод анализа переходных процессов используется в основном в тех случаях, когда исследуемая цепь имеет невысокий порядок сложности, а внешнее воздействие на нее после коммутации является либо постоянным, либо гармонической функцией времени. Если внешнее воздействие на цепь после коммутации является более сложным, то определение вынужденной составляющей реакции цепи существенно затрудняется, а при повышении порядка цепи усложняется нахождение постоянных интегрирования. Значительно большие возможности представляет операторный метод анализа переходных процессов, основанный на применении преобразования Лапласа.

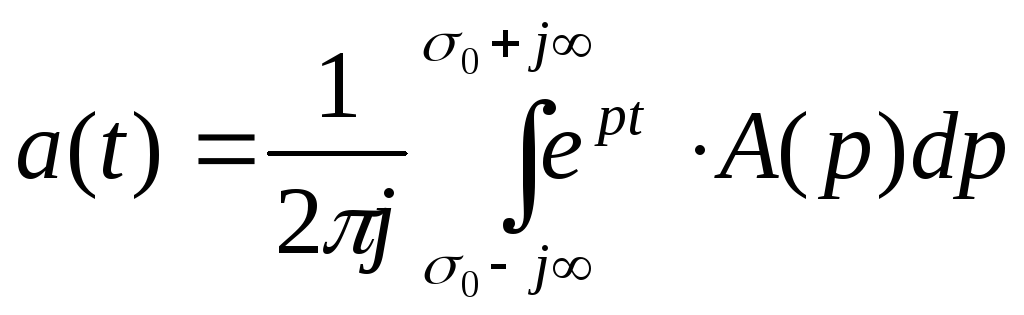Операторный метод относится к символическим методам, в которых операции над функциями времени заменяются операциями над их символами (изображениями). Взаимное соответствие между функцией времени и ее изображениемустанавливается с помощью прямогои обратногопреобразований Лапласа и указывается знаком соответствия.

Функция называется операторным изображением функции. Исходная функция временипо отношению к своему операторному изображению называется оригиналом. Комплексное числоназывается оператором преобразования Лапласа.

Основные этапы анализа переходных процессов в линейных цепях с помощью операторного метода состоят в следующем.

Анализ цепи до коммутации и определение независимых начальных условий. Выполняется так же, как и при использовании классического метода анализа переходных процессов.

Составление операторной схемы замещения цепи после коммутации. Составление операторной схемы замещения цепи производится непосредственно по схеме цепи для мгновенных значений путем замены каждого идеализированного пассивного элемента его операторной схемой замещения и представления токов и напряжений идеализированных источников тока или напряжения их операторными изображениями.

Составление уравнений электрического равновесия цепи в операторной форме. Система уравнений электрического равновесия цепи в операторной форме формируется непосредственно по операторной схеме замещения цепи.

Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений.

Определение оригиналов искомых токов и напряжений. Как правило, определение оригиналов искомых токов и напряжений производится путем применения таблиц обратного преобразования Лапласа.

Операторные схемы замещения пассивных двухполюсников приведены ранее. При анализе переходных процессов они соответствуют нулевым начальным условиям. Если в рамках решаемой задачи двухполюсник находится при ненулевых начальных условиях, то его операторная эквивалентная схема должна содержать независимый источник тока или напряжения, характеризующий начальные запасы энергии в цепи.

В связи с этим при ненулевых начальных условиях существуют параллельная (рис. 3.63) и последовательная (рис. 3.64) операторные эквивалентные схемы ёмкостного элемента, содержащие независимый источник тока или напряжения, характеризующий начальные запасы энергии в ёмкости.

Рис. 3.63	Рис. 3.64

Аналогично, при ненулевых начальных условиях существуют последовательная (рис. 3.65) и параллельная (рис. 3.66) операторные эквивалентные схемы индуктивного элемента, содержащие независимый источник напряжения или тока, характеризующий начальные запасы энергии в индуктивном элементе.

Рис. 3.65	Рис. 3.66

Пример. Для цепи, схема которой приведена на рис. 3.67, найти

Рис. 3.67	Рис. 3.68

зависимость тока и напряженияна индуктивности от времени при. ЭДС идеализированного источника постоянного напряженияприскачком изменяется отдо, т.е.

Анализируя процессы в цепи до коммутации, определяем начальное значение тока индуктивности . Для построения операторной схемы замещения цепи после коммутации (рис. 3.68) заменяем идеализированные пассивные элементы их операторными схемами замещения, а ЭДС идеализированного источника напряжения- операторной ЭДС. Используя метод контурных токов, составим систему уравнений электрического равновесия цепи в операторной форме

где . Решая эту систему уравнений, получаем операторные изображения искомого тока

и напряжения

Преобразуем полученные выражения к такому виду, при котором для выполнения обратного преобразования Лапласа можно было бы воспользоваться таблицами.

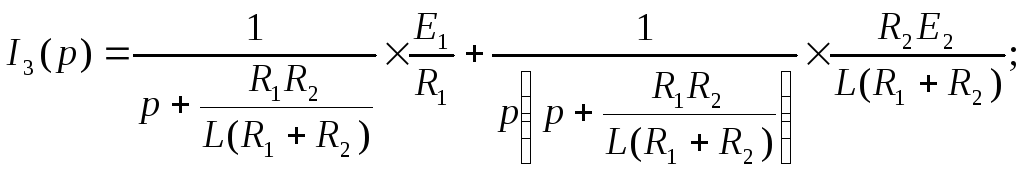
Учитывая, что и, находим выражения для искомых тока и напряжения на индуктивности при:

где - постоянная времени рассматриваемой цепи.

Как следует из полученных соотношений, в начальный момент времени ток индуктивности сохраняет то же значение, что и до коммутации , а затем плавно изменяется, стремясь к. Напряжение на индуктивности в начальный момент времени скачком изменяется от нуля до, а затем плавно уменьшается до нуля.

Нетрудно заметить, что в начальный момент времени ток и напряжение индуктивности принимают такие значения, которые они имели бы в случае, если индуктивность была заменена идеализированным источником тока, ток которого.