2.9. Передаточная функция и ее связь с дифференциальным уравнением,

с временными и частотными характеристиками электрической цепи

На рис. 2.23 показан четырехполюсник (рис. 2.23а), представляющий собой исследуемую схему, схема аналитических преобразований входного сигнала (рис. 2.23б), схема аналитических преобразований схемных функций (рис. 2.23в) и схема аналитических преобразований выходного сигнала(рис. 2.23г).

а
б	в	г
Рис. 2.23

На рис. 2.23 использованы следующие обозначения: - входной сигнал;- выходной сигнал; символомобозначено прямое преобразование Лапласа; символом- прямое преобразование Фурье; символомобозначено обратное преобразование Лапласа; символом- обратное преобразование Фурье.

Непосредственно выражение выходного сигнала можно найти через переходную характеристикус помощью интеграла Дюамеля

;

и через импульсную характеристику с помощью интеграла свертки

;

.

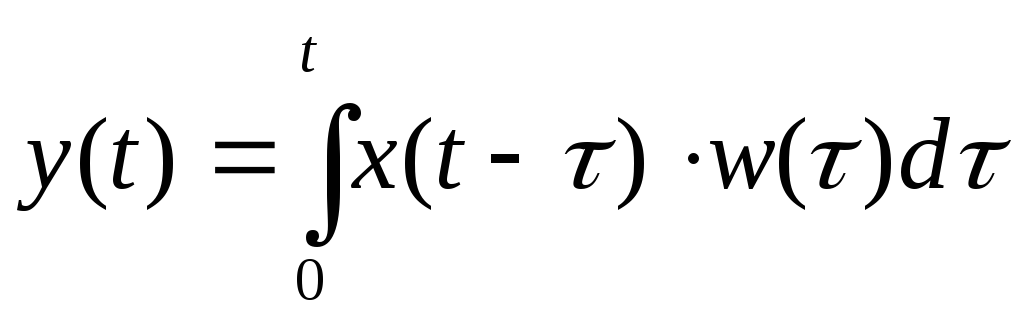Глава 3 анализ и расчет линейных цепей переменного и постоянного тока

3.1. Основные методы расчета линейных цепей Метод баланса мощностей

Так как каждая электрическая цепь передает энергию от источника к приемнику, то в соответствии с законом сохранения энергии сумма мощностей, развиваемых независимыми источниками тока и ЭДС, равна сумме мощностей, потребляемой приемниками энергии. Так составляется баланс мощностей . В левой части уравнения баланса – алгебраическая сумма мощностей источников. В правой части – арифметическая сумма мощностей приемников.

Баланс мощностей используется для проверки правильности расчета электрической цепи. Для источника ЭДС - . Для источника тока -. Для приемника -.

Правила получения положительных и отрицательных значений мощностей источников энергии иллюстрируется рис. 3.1

Положительная мощность
Отрицательная мощность
Рис. 3.1

Если исходная схема была преобразована, то по окончании ее рассмотрения для составления баланса мощностей необходимо вернуться к исходной схеме.

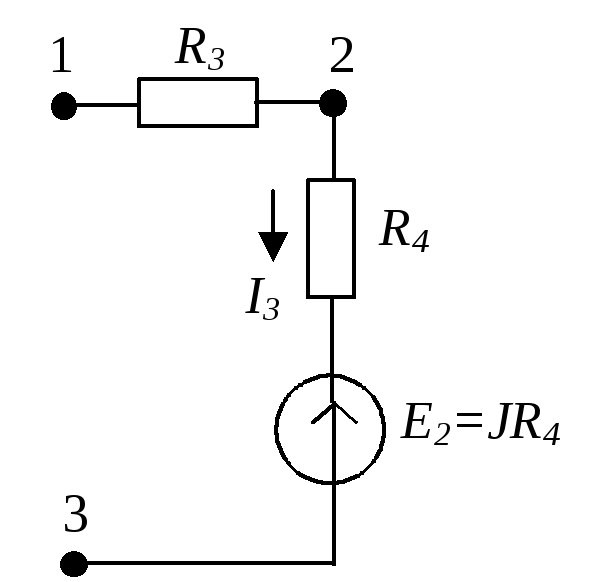
Рассмотрим пример получения баланса мощностей для схемы, приведенной на рис. 3.2.

	Количество узлов в этой схеме , следовательно, количество уравнений по первому закону Кирхгофа равно:
Рис. 3.2

Количество ветвей в рассматриваемой схеме . Одна из них – ветвь с источником тока, поэтому она не учитывается при определении количества уравнений по второму закону Кирхгофа. Тогда количество уравнений по второму закону Кирхгофа.

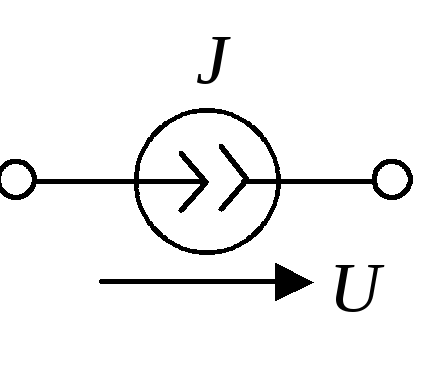
Для их составления осуществим эквивалентное преобразование (рис. 3.3) источника тока в источник ЭДС(ветвь 2-3):

	Тогда можно составить уравнения по второму закону Кирхгофа: Уравнения баланса мощностей, составленные по исходной схеме (рис. 3.2):
Рис. 3.3

Таким образом, эквивалентный источник энергии с внутренним сопротивлениеми мощностьюработает на эквивалентную нагрузку с сопротивлением, потребляющую мощность(рис. 3.4).
	Рис. 3.4

Из баланса мощностей следует правило определения передачи оптимальной мощности в нагрузку. Так как , тои.

Оптимальная (максимальная) мощность , передаваемая в нагрузку, получается при сбалансированных (равных)сопротивлениях источника и нагрузки:. Таким образом, мощность источника распределяется поровну наи.