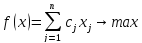1

Билет 1. Формулировка и различные формы записи задачи линейного программирования.

Линейное программирование - это раздел высшей математики ,посвященный решению задач, связанных с нахождением экстремумов функции нескольких переменных при наличии ограничений на переменные.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования.

Построение математической модели экономической задачи включает следующие этапы:

1. Выбор переменных задачи

2. Составление системы ограничений

3. Выбор целевой функции

Переменными задачи называются величины , которые полностью характеризуют экономический процесс. Их обычно записывают виде вектора .

Система ограничений включает в себя систему уравнений и неравенств ,которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий , например положительности переменных и т.п.

Целевой функцией называют функцию переменных задачи ,которая характеризует качество выполнения задачи и экстремум которой требуется найти.

Общая формулировка задач линейного программирования:

Найти , которое удовлетворяет системе линейных ограничений и обеспечивает экстремальное (max или min) значение целевой функции.

Ограничения могут быть сформулированы в виде неравенств или равенств. В зависимости от этого различают следующие формы записи задачи линейного программирования:

1. Общая форма записи.

Дана система m линейных ограничений, где s равенств и (m-s) неравенств.

s равенств

(1)

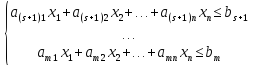(m-s) неравенств

(2) m

(3)

Требуется найти такое решение системы ограничений (1) , удовлетворяющее условиям (2), на котором линейная функция f достигает max (min).

2. Симметричная форма записи. Используется при решении злп графическим методом.

(3)

1. 

2. 

(3)

1. 

2. 

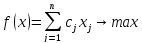
3. Каноническая форма записи отличается тем, что система ограничений (1) содержит только равенства, и ищем только max. Используется при решении злп симплексным методом.

3. 

1. 

2. 

Определения:

Решение , координаты которого удовлетворяют системам ограничений (1) и (2), называется допустимым решением задачи.

Множество всех допустимых решений задачи называется областью допустимых решений задачи.

Допустимое решение , для которого линейная функция достигает max (min) называется оптимальным решением задачи.