10

10.Теорема о существовании опорного решения

Если система линейный уравнений (1) имеет хотя бы одно допустимое решение( совместна в ОДР), то среди этих решений есть хотя бы одно опорное.

Док-во: систему лин. Уравнений (1) запишем в виде векторного ур-я

(1’)

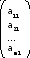
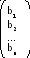
Пусть ранг системы векторов-коэффициентов r ( , , …, )= r и , , …, - базис системы векторов-коэфф-в. В общем решении системы (1) x_{1, …,}x_r - базисные, а x_r+1…., x_n- свободные неизвестные. Из общего реш-я, положив все свободные неизвестные равными 0, мы можем записать базисное реш-е:

= , , …, , 0,0,…,0)

Если числа b_i,…,b_r , то - допустимое – X опорное

Надо док-ть, что система (1) имеет опорное реш-е данного вида

Пусть = , , …, , 0,0,0) – допустимое реш-е сист (1)

Возможны два случая:

1. k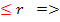последних нулевых координат у n-r. Это означает, что реш-е – допустимое и базисное реш-е, т.е. реш-е опорное.

2. k> r, тогда имеет <n-r последних нулевых координат, т.е. не является базисным реш-м

= , , …, , 0,..,0) – не базисное, не опорное (0,..,0<n-r) (это альфа).

– реш-е (1): (1ая – а, 2ая – альфа)

, , …, - л.з., k>r нетрив. лин. комбинация =

Утв-е: Среди ненулевой коэф-т

Противное: … =: нетрив. лин. комбинация, т.к. ненулевой кэф-т – противоречие ( , , …, – базис, лин. независим. система в-вов)

) -  λ: (₁- λc₁)+...+ (_r- λc_r)+ (_r+1- λc_r+1)+...+ (_k- λc_k)=

(в скобках альфа) => = (₁- λc_1,…,r- λc_r,r+1- λc_r+1,.., _k- λ_ck,0,...,0) – есть реш-е (1)

Вычислим все отношения ,…, и возьмем среди этих чисел наименьшее. Пусть λ=, тогда к-ая координата : _k- λ_ck=_k- с_к=0, а все остальные координаты

В решении число нулевых (свободных переменных) координат стало хотя бы на 1 больше. Если это число останется <n-r, то процедуру надо повторить до тех пор, пока не придем к вектору, у которого последние (n-r) координат будут равны 0, т.е. найдем опорное реш-е.