
- •В.В. Черепанов, Н.С. Бакшаева
- •Киров 2004
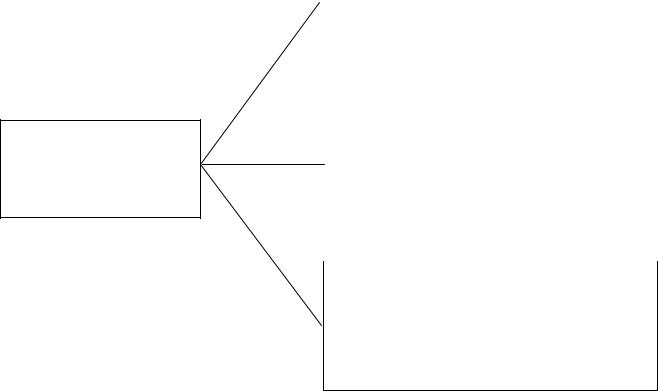
- •Рис.2.1. Классификация методов расчета установившихся режимов.
- •Здесь матрица
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •“Прикладные математические методы ч.1”
- •Литература
- •Оглавление
сматривающих либо преобразование исходных уравнений, либо те или иные предварительные изменения в исследуемой сети.
Первые попытки расчета установившихся режимов на ЭВМ были сделаны на основе метода контурных токов. Но широкого распространения этот метод не получил из-за сложности и неоднозначности процедуры выделения независимых контуров, трудностей учета трансформаторов с неноминальными коэффициентами трансформации и режимных ограничений, а также затруднений, связанных с изменением конфигурации сети в процессе расчета.
Последний из рассмотренных методов также не получил широкого распространения. Он применяется для расширения специфичных задач, таких как определение пределов мощности и устойчивости электропередач, вычисление параметров аварийных и послеаварийных режимов при расчетах устойчивости электрических систем, нахождение распределения токов короткого замыкания и т.д.
Сейчас основным методом, используемым для составления системы уравнений установившегося режима, является метод узловых напряжений.
Уравнение Кирхгофа
é |
M |
ù |
& |
ù |
= |
é |
I& ù |
|
ê |
|
ú |
éI |
ê |
|
ú |
||
|
ë û |
|
|
|||||
ëM Zв û |
|
|
|
ëEk û |
||||
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
Контурное уравнение |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
[Z ]I |
|
|
= |
|
E |
|
|
|
|
|
|
|
|
|
|
éM-1ù |
|
J |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
é |
|
-[N ][Z ê] |
|
a |
|
ú |
é |
ù |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
é& |
|
ù |
|
|
|
& |
|
|
ù |
|
|
|
|
|
|
в ê |
|
|
|
|
& |
|
|
|
|
|
|||||||||||
|
|
|
|
|
k ë |
|
k |
û ë |
|
|
|
|
k û |
|
|
|
|
|
|
0 ú |
ë û |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
|
|
|
|
] |
|
|
|
|
|
|
|
[ |
|
|
][ |
|
|
][ |
|
|
éM-1 |
ù |
|
|
|
|
||||||||
é |
& |
|
ù |
|
|
|
|
|
|
& |
ù |
|
|
|
|
|
|
|
|
ê |
|
] |
a |
ú |
é |
& |
ù |
|
||||||||||||||||
|
= У |
|
|
é |
|
- У |
|
N |
Z |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ë |
J |
k |
û |
k |
|
ë |
E |
k û |
k |
в ê |
|
|
0 ú ë |
J |
û |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Узловое уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
é |
У |
|
ù |
|
|
& |
|
|
ù = |
|
|
& |
ù |
-[M |
é |
|
-1 |
ù |
|
& |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
éU |
D |
|
éJ |
]Z |
в |
|
éEù |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
ë |
|
|
у û |
ë |
|
û |
|
|
ë û |
|
|
|
|
ë |
|
û ë û |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
& |
|
|
|
-[Z ][M |
é |
|
-1ù |
|
& |
û |
|
|
|
|
|
|
|
|
|||||||||||
|
|
ëUD û =[Z |
|
]ëJû |
ë]Zв |
û |
ëE |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
é |
|
|
|
ù |
|
|
|
|
|
|
é |
|
|
ù |
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
ù |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Уравнение токов в ветвях |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
é& |
ù |
|
=[C ]- |
é |
&ù |
|
|
|
é & |
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
ëIû |
|
ëJû |
+ Уij ëEû |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
припредставлениинагрузки
J& =const ; Zн =const
Рис.2.1. Классификация методов расчета установившихся режимов.
Методы решения линейных уравнений установившегося режима можно разделить на две группы: точные и итерационные, или приближенные.
25
Точными методами называются такие, которые в предположении, что все вычисления ведутся точно (без округлений) позволяют получить точные значения неизвестных в результате конечного числа операций. Практически же все вычисления ведутся с округлением, поэтому и значения неизвестных, полученные точным методом, будут содержать погрешности. Поэтому термин “точные методы” условен. Иногда в литературе точные методы называют прямыми методами расчета.
Из точных методов ниже рассмотрены метод Гаусса и методы, предусматривающие преобразование уравнений состояния.
Итерационными (приближенными) методами называют такие, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы уравнений лишь с заданной точностью. Точное решение систем в этом случае может быть получено теоретически какре зультат бесконечного итерационного процесса. В данном учебном пособии рассмотрено два итерационных метода: простая итерация и метод Зейделя.
2.2. Расчет режима сети, содержащей только источники тока.
При расчетах могут иметь место два случая:
1. Схема замещения сети не содержит замкнутых контуров. Граф такой сети образует дерево. Матрица соединений для дерева[Ma ]является
квадратной и имеет обратную. Поэтому в рассматриваемом случае узловое уравнение можно непосредственно использовать для определения матрицы токов ветвей. То есть, оно может быть разрешено относительно токов:
é |
& |
ù |
é -1ù |
é |
& |
ù |
|
é |
& |
ù |
|
|
|
=ëMa û |
|
|
|
(2.1) |
|||||||
ëI |
û |
ëJû |
=[C0 ë]Jû. |
|||||||||
Здесь матрица |
|
|
[C |
|
=] |
éM-1 |
|
|
|
|
||
|
|
|
о |
ù |
|
|
|
|||||
|
|
|
|
|
|
ë |
a |
û |
|
|
|
|
определяет распределение токов по разомкнутой схеме и называется матрицей коэффициентов распределения токов для разомкнутой схемы в виде дерева. Ее строки соответствуют ветвям схемы, а столбцы-независимым узлам. Каждый столбец i матрицы определяет путь графа от узлаi до узла баланса схемы. Коэффициенты распределения тока могут иметь здесь одно из трех значений: +1, -1, 0. Положительная единица в столбцеi означает, что соответствующая ветвь входит в состав данного пути с тем же направлением, отрицательная – с противоположным. Нуль показывает, что данная ветвь не входит в состав данного пути графа. Каждый путь графа в данном случае со-
ответствует пути прохождения рассматриваемого задающего тока отсо ответствующего узла к узлу баланса. Матрица [C0 ] может быть составлена непосредственно по схеме, и наоборот, по [C0 ] разомкнутая схема может быть восстановлена.
26
Матрица напряжений на ветвях связана с матрицей токов в ветвях уравнением (1.8).Учитывая, что в рассматриваемом случае э.д.с. в ветвях отсутствуют, напряжения на ветвях определяются из этого уравнения следующим образом:
éU ù = [U] = éZ |
ù éIù . |
(2.2) |
||||||
ë |
& |
В û |
ë |
& |
В û ë |
& |
û |
|
|
|
|
|
|||||
Во многих случаях расчета узловые напряжения целесообразно опре- |
||||||||
делять относительно базисного |
узла. При |
этом |
узловые напряжения |
|||||
U& D определяют суммарные падения напряжения от каждого из независимых узлов схемы до базисного узла. Эти значения отличаются от напряжений относительно нейтрали U& S на величину напряжения базисного узла Uб :
& |
& |
& |
|
|
|
US |
=UD +Uб . |
|
|
|
|
Матрица узловых напряжений |
в |
é |
& |
ù |
может |
разомкнутой схемеU |
Da û |
||||
|
|
ë |
|
|
|
быть определена по матрице коэффициентов распределения для токов[C0 ] и матрице напряжений не ветвях
é & |
ù |
= |
é -1 |
ù é & ù |
é & ù |
, |
(2.3) |
ëUDa û |
ëMat |
û ëUВ û |
= [C0t ]ëUВ û |
||||
Следовательно, матрица [C0 ]применима и для нахождения узловых напряжений. Это объясняется тем, что столбцы матрицы [C0t ] определяют
пути графа, по которым происходит суммирование напряжений на ветвях при получении узловых напряжений относительно базисного узла.
Таким образом, режим в рассмотренном случае может быть определен по выражениям (2.1), (2.2) и (2.3).
Пример 2.1.
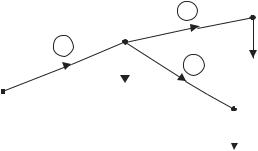
Найти токи в ветвях разомкнутой электрической сети, схема которой показана на рис.2.2., используя матричную форму записи первого закона Кирхгофа и принимая матрицу токов нагрузок равной
|
|
|
|
|
é |
|
10 |
ù |
|
|
|
& |
ù= |
ê |
|
|
ú |
. |
|
||
éI |
10 + j5 |
ú |
|
|||||||
ë |
|
у û |
ê |
|
|
|
|
|||
|
|
|
|
|
ê |
5 |
+ j5 |
ú |
|
|
|
|
|
|
|
ë |
û |
|
|
||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
|
& |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
& |
|
|
|
|
|
Ι у 2 |
|
|
|
|
|
|
|
||||
4 |
|
|
|
Ι у 1 |
|
|
3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
&Ι у 3
Рис.2.2.
27
Токи в ветвях могут быть найдены из уравнения (2.1):
éë&Iùû =[С0 ]éëJ&ùû.
Матрица задающих токов éJ&ù равна матрице токов нагрузок é&I ù , взя-
ë û ë у û
той с противоположная знаком:
éJù |
=-éI |
ù. |
|||
ë |
& |
û |
ë |
& |
у û |
|
|
||||
Матрица коэффициентов распределения токов в разомкнутой схеме |
|||||
[С0 ] находится в соответствии с изложенным выше правилом непосредственно по схеме
|
é-1 -1 |
-1ù |
||
[С0 =] |
ê |
0 |
-1 |
ú |
ê |
0 ú . |
|||
|
ê |
0 |
0 |
ú |
|
ë |
-1û |
||
Правильность определения [С0 ] |
|
может |
быть проверена путем умно- |
|
жения ее на матрицу [Ma ]. Их произведение, в соответствии с определением обратной матрицы, должно быть равно единичной матрице.
|
|
|
|
|
é-1 -1 -1ù é-1 1 1 ù é1 0 0ù |
||||||||||||||
[ |
С |
M |
= |
ê |
0 -1 0 ú× |
ê |
0 -1 0 |
ú= |
|
ê0 1 0ú. |
|||||||||
|
0 ][ |
a |
|
]ê |
|
|
ú ê |
|
|
|
ú |
ê |
|
|
ú |
||||
|
|
|
|
|
ê |
0 0 |
ú ê |
|
|
|
ú |
|
ê |
|
|
ú |
|||
Следовательно, |
|
|
|
|
ë |
-1û ë |
0 0 -1û ë0 0 1û |
||||||||||||
|
|
|
|
|
é-1 |
-1 |
-1ù |
|
10 |
|
|
é25 + j10 |
|
||||||
|
|
|
|
|
|
é |
ù |
|
ù |
||||||||||
|
& |
|
|
& |
|
ê |
0 |
|
|
ú |
ê |
|
ú |
|
ê |
10 + j5 |
ú |
||
ëéIûù =[С0 |
ëé]Jûù |
=-ê |
-1 0 ú |
× ê10 + j5ú = |
ê |
ú. |
|||||||||||||
|
|
|
|
|
|
ê |
0 |
|
|
ú |
ê |
5 + j5 |
ú |
|
ê |
5 + j5 |
ú |
||
|
|
|
|
|
|
ë |
0 -1û ë |
û ë |
û |
||||||||||
2. Схема замещения сети содержит замкнутые контуры. Предполо- |
|||||||||||||||||||
жим, что известна |
матрица |
узловых |
|
|
|
|
é & |
|
|
ù |
. Тогда матрица |
||||||||
|
напряженийU |
D û |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
||
напряжений на ветвях, представляющая собой разности потенциалов между вершинами соответствующих ветвей, может быть определена путем умноже-
é & |
ù |
на транспонированную матрицу соединений [Mt ]: |
|
||
ния матрицы ëUD û |
|
||||
|
|
é & ù |
é & |
ù |
(2.4) |
|
|
ëUВ û |
= [Mt ]ëUD û . |
||
Применение матрица [Mt ] в данном случае возможно, т.к. ее строки
определяют узлы, являющиеся начальными и конечными вершинами каждой ветви. Используя уравнения (1.8) и (2.4) можно получить уравнение, связы-
|
|
|
|
é |
& |
ù |
с матрицей токов в ветвях: |
|
|
|
вавшее матрицу узловых напряжений ëUD û |
|
|
||||||||
|
|
|
é & |
ù |
|
é & |
ù é&ù é & ù |
|
|
|
|
|
|
[Mt ]ëUD û = |
ëZВ û ëIû - ëEû . |
|
|
|
|||
Это |
уравнение можно решить |
|
|
é |
& |
ù |
, т.к. |
|||
относительно матрицы токовI |
û |
|||||||||
|
|
|
|
|
|
|
ë |
|
|
|
|
& |
ù |
является квадратной и неособенной: |
|
|
|
||||
матрица éZ |
|
|
|
|||||||
ë |
|
в û |
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
é&ù |
é & |
ù |
|
|
] |
é |
& |
ù |
é & |
ù |
|
|
|
|
|
|
|
||||||
|
|
|
ëIû = |
ëУВ û([Mt |
ëUD |
û |
+ ëEû) . |
|
|
|
|
|
||||||||||||||
é & ù |
|
é & -1ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь ëУВ û |
= ëZВ û - матрица проводимостей ветвей. |
|
|
|
||||||||||||||||||||||
Поскольку, в рассматриваемом случае э.д.с, в ветвях отсутствуют, это |
||||||||||||||||||||||||||
выражение можно упростить: |
= |
éУ ù M |
t ] |
éU ù |
= é |
У |
|
ù éU ù |
|
(2.5) |
||||||||||||||||
|
|
|
éIù |
|
|
|||||||||||||||||||||
|
|
|
ë |
& |
û |
|
ë |
& |
|
|
ë |
& |
D û ë |
& |
В |
û ë |
& |
В |
û |
|
|
|||||
|
|
|
|
|
В û[ |
|
|
|
|
|
|
|||||||||||||||
С учетом последнего выражения узловое уравнение можно записать |
||||||||||||||||||||||||||
следующим образом: |
=[Μ] |
|
|
|
|
|
|
|
|
[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
é&ù |
é |
&ù |
|
|
é & |
|
ù |
|
é |
& |
ù |
= |
é |
& |
|
ù |
é & |
ù |
(2.6) |
|||||
|
|
ëJû |
ë |
Ιû=[Μ]ëУВ û |
Μt ]ëU |
û |
ë |
Уу û |
ëU |
û . |
||||||||||||||||
Выражение (2.6) является матричным узловым уравнением для слож- |
||||||||||||||||||||||||||
ной схемы без э.д.с, в ветвях. Матрица |
|
|
|
|
[Mt |
] |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
é |
& |
ù |
= |
[M] |
é & |
|
ù |
|
|
|
|
|
|
|
|
(2.7) |
||||||
|
|
|
|
ë |
Уу |
û |
ëУВ û |
|
|
|
|
|
|
|
|
|||||||||||
называется матрицей узловых проводимостей схемы. |
|
|
|
|
|
|
|
|||||||||||||||||||
Матрица é |
& |
ù |
квадратная, |
симметричная, |
неособенная, |
порядка n. |
||||||||||||||||||||
У |
||||||||||||||||||||||||||
ë |
|
у û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это матрица коэффициентов узловых уравнений. По ее главной диагонали расположены суммарные значения проводимостей всех ветвей, соединенных с соответствующим узлом схемы, а на пересечении строкиi и столбца j - проводимость ветви с вершинамиi и j, взятая с обратным знаком. Матрица
é |
& |
ù |
может быть составлена непосредственно по схеме(без взаимных со- |
||||||||||||||||||||||||||
У |
|||||||||||||||||||||||||||||
ë |
|
у û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противлений). И |
наоборот, по |
матрице |
é |
|
& |
|
ù |
можно составить |
схему заме- |
||||||||||||||||||||
У |
|
||||||||||||||||||||||||||||
щения. |
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
у û |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Дпя схемы |
|
без взаимных |
сопротивлений |
|
узловое уравнение(2.6) по- |
|||||||||||||||||||||
зволяет определить матрицу |
é |
& |
ù |
по матрице |
é |
|
& |
ù |
задающих токов: |
||||||||||||||||||||
ëUD û |
ë |
Уû |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
& |
|
ù = |
é |
|
& |
-1ù |
|
|
& |
|
|
|
& |
|
ù |
& |
ù. |
|
|
(2.8) |
||
|
|
|
|
|
|
éU |
D |
ë |
У |
у û |
éJù |
|
=éZ |
у |
éJ |
|
|
||||||||||||
|
|
|
|
|
|
ë |
|
û |
|
|
ë û |
|
ë |
|
|
û |
ë û |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
& |
ù= |
é |
|
& |
|
-1 |
ù |
|
|
|
|
|
|
|
(2.9) |
||
|
|
|
|
|
|
|
|
|
|
éZ |
ë |
У |
у |
û |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ë |
|
у û |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
- матрица узловых сопротивлений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Матрица éZ& |
у |
ù квадратная, симметричная, |
неособенная, порядка n. По |
|||||||||||||||||||||||
|
|
|
ë |
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
ù схемы, т.е. |
ее главной диагонали расположены входные сопротивления éZ |
ii |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
û |
|
эквивалентные сопротивления между базисным и каждым из независимых узлов. На пересечении строки i и столбца j находится общее для узловi и j сопротивление Z& ij относительно базисного узла.
Входное сопротивление Z& ii определяет напряжение U& i между i-м и ба-
зисным узлом схемы, обусловленное задающим током J&i узла i .
29

|
|
& |
& |
|
Общее сопротивление Zij |
определяет напряжение U j между j -м и ба- |
|||
|
|
|
& |
& |
зисным узлами, обусловленное задающим током Ji узла i или напряжение |
Ui |
|||
|
|
|
& |
|
между i-м и базисным узлами, обусловленное задающим током J j узла j. |
|
|||
|
& |
ù непосредственно по схеме составлена быть не может. |
|
|
Матрица éZ |
|
|||
ë |
|
у û |
|
|
Таким образом, режим в рассматриваемом случае может быть рассчи-
тан по выражениям (2.8), (2.4) и (2.5).
Пример 2.2.
Найти узловые напряжения в схеме, показанной на рис.2.3. Сопро-
тивления ветвей схемы равны: |
|
|
|
|
|
|
|
& |
|
& |
= |
& |
= 1; |
& |
= 4. |
ZВ1 = 1; |
ZВ2 |
2; ZВ3 |
ZВ4 |
||||
& |
= |
& |
|
& |
|
|
|
Токи нагрузок равны: Iу1 |
2; Iу2 |
=1; Iу3 =3. |
|
|
|||
Поскольку э.д.с. ветвей отсутствуют, то для определения узловых напряжений может быть использовано матричное уравнение (2.8).
|
& |
ù |
= |
é |
& |
-1ù |
& |
|
& |
& |
éU |
ë |
У |
|
éJù |
=éZ |
ù éJù. |
||||
ë |
|
D û |
|
|
у û ë û |
ë |
|
у û ë û |
||
4
1
2
3
5
Рис.2.3.
Составим матрицу сопротивлений ветвей схемы
|
|
|
é1 |
|
ù |
|
|
|
ê |
2 |
ú |
|
|
|
ê |
ú |
|
éZ |
|
1 |
|||
ù = ê |
ú |
||||
ë |
& |
В û |
ê |
|
ú |
|
4 |
||||
|
|
|
ê |
ú |
|
|
|
|
ê |
|
ú |
|
|
|
ë |
|
4û |
Эта матрица имеет диагональную форму, поэтому
30
|
|
|
|
|
|
é1 |
|
|
|
|
|
|
|
|
|
|
|
|
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
1 |
|
|
|
|
|
|
|
|
|
ú |
é1 |
|
|
|
|
|
|
|
|
|
ù |
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
ê |
|
2 |
|
|
|
|
|
|
|
|
|
ú |
ê |
|
0,5 |
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
1 |
|
|
|
|
|
|
|
ú |
ê |
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
é & |
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú = ê |
|
1 |
|
|
|
|
|
|
|
|
ú . |
|
|
|
||||
|
|
|
ëУВ û = ê |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
ú |
ê |
|
0, 25 |
|
|
|
|
|
ú |
|
|
|
|||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
ê |
|
|
|
|
|
|
ú |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
ê |
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ë |
|
|
|
|
|
|
0, 25û |
|
|
|
|||||||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
4 û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Матрица узловых проводимостей é |
& |
ù может быть определена непо- |
|
|||||||||||||||||||||||||||||||
У |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
у û |
|
|
|
|
|
|
|
|
|
|
|
|
средственно по схеме замещения с помощью приведенных выше сведений о |
|
|||||||||||||||||||||||||||||||||
ее структуре: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
é(1 + 0, 25) |
|
|
|
|
-0, 25 |
|
|
|
0 |
ù |
|
é 1, 25 |
-0, 25 |
0 |
ù |
|
||||||||||||||
é |
& |
ù= |
ê |
-0, 25 |
|
(0,5 + 0, 25 + 0, 25) |
-0, 25 |
ú |
= |
ê |
-0, 25 |
1, 0 |
-0, 25 |
ú |
. |
|||||||||||||||||||
У |
ê |
|
ú |
ê |
ú |
|||||||||||||||||||||||||||||
ë |
|
у û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ê |
0 |
|
|
|
|
|
|
-0, 25 |
|
|
|
(1 + 0, 25) |
ú |
|
ê |
|
|
0 |
|
-0, 25 |
1, 25 |
ú |
|
|||||||
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
û |
|
ë |
|
|
|
û |
|
|||||||||||||
В качестве базисного принят четвертый узел. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Зная матрицу |
é |
& |
ù , |
найдем |
обратную матрицу |
|
& |
|
|
ù , |
используя из- |
|
|
|||||||||||||||||||||
У |
éZ |
у |
|
|
||||||||||||||||||||||||||||||
вестное выражение |
ë |
|
у û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
û |
|
|
|
|
||||||||
|
|
|
|
|
|
аij-1 =D-1 M ji (-1 ()i+ j) , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где D - определитель матрицы [A]; Mji - минор для элемента а ji матрицы |
|
|
||||||||||||||||||||||||||||||||
[A], т.е. определитель матрицы на единицу меньшего порядка, полученнтй |
|
|
||||||||||||||||||||||||||||||||
из матрицы [A] путем исключения строки j и строки i. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
для вычисления членов обратной матрицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
1 |
|
& |
|
|
(i+ j ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
а ij |
= |
|
|
|
|
M ji (-1 |
) . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Предварительно вычислим определитель |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
é 1, 25 |
-0, 25 |
|
0 |
|
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
D = |
ê |
|
|
1 |
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ê-0, 25 |
|
|
|
-0, 25ú =1, 25×1×1, 25 -(-0, 25)(0, 25)×1, 25 - |
|
|
|
||||||||||||||||||||||||||
|
|
|
ê |
0 |
-0, 25 |
1, 25 |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
-(-0, 25)(-0, 25)×1, 25=1,562 -0, 0782 -0,0782 =1, 406.
Для матрицы третьего порядка
31
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
a |
22 |
|
a23 |
|
|
|
|
|
|
a21 |
a23 |
|
|
|
|
a21 |
|
a22 |
|
|
ù |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
& |
|
|
|
& |
|
|
|
|
|
|
- |
|
& |
& |
|
|
|
|
|
|
|
|
& |
|
|
& |
|
|
ú |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
& |
|
|
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
& |
|
|
& |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
a32 |
|
a33 |
|
|
|
|
|
|
a31 |
a33 |
|
|
|
|
a31 |
|
a32 |
|
|
ú |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ê |
|
|
|
& |
|
& |
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|
|
& |
|
& |
|
|
ú |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
& |
|
|
é |
|
& |
-1ù |
|
|
|
|
|
a12 |
a13 |
|
|
a11 |
a13 |
|
|
|
|
|
|
|
|
|
a11 |
|
a12 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
éZ |
ù |
= |
ë |
У |
|
у |
û |
= |
|
|
ê- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
ú= |
|
|
|
|||||||||||||
ë |
|
|
у û |
|
|
|
|
|
|
|
D ê |
|
|
a32 |
a33 |
|
|
a31 |
a33 |
|
|
|
|
|
|
|
|
|
a31 |
|
a32 |
ú |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
& |
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|
|
& |
|
& |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
a12 |
|
a13 |
|
|
|
|
|
a11 |
a13 |
|
|
|
|
a11 |
|
a12 |
|
|
ú |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
& |
|
|
|
& |
|
|
|
|
|
|
- |
|
& |
& |
|
|
|
|
|
|
|
|
& |
|
|
& |
|
|
ú |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
a |
22 |
|
a23 |
|
|
|
|
a21 |
a23 |
|
|
|
|
a21 |
|
a22 |
|
|
û |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
& |
|
|
|
& |
|
|
|
|
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
& |
|
|
& |
|
|
ú |
|
|
|
|
|
|
||||
|
|
|
|
|
|
é |
|
|
1,0 |
|
|
|
-0, 25 |
|
- |
|
-0, 25 |
-0, 25 |
|
|
|
|
|
|
-0, 25 |
|
1 |
|
|
|
|
|
ù |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ê |
|
-0, 25 |
|
|
1, 25 |
|
|
0 |
|
1, 25 |
|
|
|
|
|
|
|
0 |
|
|
-0, 25 |
|
|
ú |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
ê |
|
|
|
-0, 25 |
|
|
0 |
|
|
|
|
|
1, 25 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
-0, 25 |
|
ú |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= |
|
|
|
|
ê- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
ú= |
|
|
||||||||||||||||||||||||||||||||||||
1, 406 |
|
-0, 25 |
|
1, 25 |
|
|
|
|
0 |
|
1, 25 |
|
|
|
|
|
1, 25 |
|
-0, 25 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ê |
|
-0, 25 |
|
|
|
0 |
|
|
|
|
|
|
1, 25 |
0 |
|
|
|
|
|
|
|
1, 25 |
|
-0, 25 |
|
|
ú |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
ê |
|
|
1,0 |
|
|
|
-0, 25 |
|
|
|
-0, 25 |
-0, 25 |
|
|
|
|
|
|
-0, 25 |
|
1,0 |
|
|
ú |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
é1,1875 |
|
|
0,312 |
|
0, 0625ù |
é 0,846 |
|
|
0, 222 |
|
0, 0445ù |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ê |
0,312 |
|
|
1,562 |
|
0,312 |
ú |
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
||||||||||||||||||||||
= |
|
|
ê |
|
|
|
ú |
=ê 0, 222 |
|
|
|
|
1,112 |
|
0, 222 |
ú . |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
1, 406 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
0,312 |
|
|
|
|
|
|
|
|
ú |
ê |
|
|
|
|
|
0, 222 |
|
0,846 |
ú |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
ë0,0625 |
|
|
|
1,1875 û |
ë0, 0445 |
|
û |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Определим матрицу |
|
é |
& |
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
ëUD û . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é 0,846 |
|
|
|
0, 222 |
0, 445ù é-2ù |
|
é2, 048ù |
|
|||||||||||||||||||||||||||||
|
|
|
|
& |
|
|
|
|
|
|
|
|
& |
|
|
ù |
|
& |
ù= |
ê |
0, 222 |
|
|
|
1,112 |
0, 222 |
ú |
× |
ê |
-1 |
ú |
=- |
ê |
2, 222 |
ú |
. |
||||||||||||||||||||||||
|
|
|
éU |
|
|
|
ù =éZ |
у |
éJ |
ê |
|
|
|
ú |
ê |
ú |
ê |
ú |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
ë |
|
D û |
ë |
|
|
û |
ë û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
0, 222 |
0,846 |
ú ê |
|
ú |
|
ê |
|
|
|
|
|
ú |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë0,0445 |
|
û ë |
-3û |
|
ë |
2,851û |
|
||||||||||||||||||||||||||||||
2.3. Расчет режима сети, содержащей только источники напряжения.
Если применение узловых уравнений было удобно при отсутствии в схеме э.д.с., то применение контурных уравнений получается более простым при отсутствии в схеме задающих токов. При расчете методом контурных токов считают, что в каждом независимом контуре схемы течет свой контурный ток &Iк . Уравнения составляются относительно контурных токов. Их число равно числу независимых контуров схемы.
За искомые переменные в этом методе принимают контурные токи. При этом токи ветвей схемы определяются как алгебраическая сумма токов
32
контуров, к которым относятся каждая из рассматриваемых ветвей. Эта операция может быть выполнена путем умножения транспонированной второй
|
|
é& ù |
матрицы инциденции [Nt ] на матрицу контурных токов ëIк û . |
||
& |
& |
(2.10) |
ëéIûù |
=[Nt ]ëéIк ûù . |
|
Действительно, каждая строка i матрицы [Nt ] |
содержит единицы в тех |
|
местах, которые имеют номера контуров, содержащих ветвь i. Знак при каждой единице показывает, совпадает направление ветви с направлением обхода соответствующего контура или противоположно ему. Поэтому матрица
[Nt ] и обеспечивает суммирование контурных токов для каждой ветви схемы.
При разделении в равенстве (2.10) матриц |
é&ù |
и [Nt ] на блоки с учетом |
|||||||||||||
ëIû |
|||||||||||||||
é |
ù |
é |
ù |
=[1], получается: |
|
|
|
|
|
|
|||||
того, что ëNbt û |
= ëNb |
û |
|
|
ù |
|
|
|
|||||||
|
|
|
|
|
éI |
|
ù |
éN |
|
|
|
|
|
||
|
|
|
|
é&ù |
ê |
& |
a |
ú =ê |
at |
|
é& |
ù |
|
||
|
|
|
|
|
ú |
|
|||||||||
|
|
|
|
ëIû = |
& |
|
|
ëIк û |
|
||||||
|
|
|
|
|
|
ú |
ë 1 |
|
û |
|
|
|
|||
|
|
|
|
|
êIb |
|
|
|
|
||||||
или отдельно для дерева |
ë |
|
|
û |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
é& |
|
ù |
|
|
|
é |
& |
ù |
|
|
|
|
|
|
|
ëIa û =[Nat ] |
ëIк û |
|
|
||||||||
и для хорд |
é& ù |
é& ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
ëIb û |
=ëIк û . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, для определения токов во всех ветвях схемы достаточно найти только контурные токи, которые (при принятых ранее условиях) совпадают с токами в хордах схемы. Этим в частности и объясняется приведенная ранее рекомендация о выборе независимых контуров схемы и их нумерации.
Из контурного уравнения (1.16) и уравнения (2.10) следует, что
|
|
é & ù é&ù |
= [N |
é & |
ù |
|
|
|
é& |
ù |
|
é & ù é & |
ù |
||||
|
[N]ëZВ û ëIû |
]ëZВ û[Nt ] |
ëIk û |
= [N]ëEû = ëEk û . |
|||||||||||||
Отсюда можно записать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
& |
ù = |
|
& |
|
|
& |
ù . |
|
|
(2.11) |
|||
|
|
|
éE |
éZ |
|
ù éI |
|
|
|||||||||
|
|
|
ë |
|
к û |
ë |
|
к û ë |
|
к û |
|
|
|
|
|
||
Здесь |
|
|
ë |
|
k û |
[ |
|
|
]ë |
|
|
В û |
[ |
|
|
t ] |
|
|
|
|
|
N |
|
|
N |
(2.12) |
|||||||||
|
|
|
éZ |
ù = |
|
éZ |
ù |
|
|
||||||||
|
|
|
|
& |
|
|
|
|
|
& |
|
|
|
|
|
|
|
- матрица контурных сопротивлений. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
& |
ù квадратная, симметричная, неособенная, порядка к. По |
|||||||||||||||
Матрица éZ |
|||||||||||||||||
ë |
|
к û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
главной диагонали этой матрицы расположены собственные сопротивления Z& ii независимых контуров i, а на пересечении строки i и столбца j находится общее сопротивление Z& ij для контуров i и j .
Уравнение (2.11) позволяет определить матрицу контурных токов по известной матрице контурных э.д.с.
33
é& |
ù |
= |
é & -1 |
ù é & |
|
ù |
= |
é |
& |
ù é & |
ù |
|
|
|
|||||||
ëIк |
û |
ëZ к |
û ëEк |
û |
ëУк û ëEк û . |
|
|
||||||||||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
& |
|
|
|
|
é & -1ù |
|
|
|
|
|
|
& |
|
|
|
|
|
|||
é |
|
|
ù |
|
|
|
[ |
|
|
] |
ù |
[ |
|
|
] |
||||||
У |
|
= |
|
Z |
|
= |
|
N |
|
N |
|
||||||||||
|
ë |
k û |
( |
|
éZ |
|
t |
) |
|
||||||||||||
ë |
|
|
k û |
|
|
|
|
|
|
ë |
|
В û |
|
|
|
||||||
(2.13)
(2.14)
- матрица контурных проводимостей.
é & ù |
квадратная, симметричная, неособенная, порядка к. По |
Матрица ëУк û |
главной диагонали этой матрицы размещены собственные проводимости У& ii контуров i, а на пересечении строки i и столбца j – взаимные проводимости У& ij контуров i и j . Собственная проводимость У& ii контура i определяет кон-
турный ток &Iкi , обусловленный контурной э.д.с. E& кi того же контура. Взаим-
ная проводимость У& ij контура j, обусловленный контурной э.д.с. E& кi контура i, или контурный ток &Iкi контура i, обусловленный контурной э.д.с. E& кj кон-
тура j.
Таким образом, при расчете режима сети в рассматриваемом случае вначале из уравнения (2.13) определяют контурные токи, а затем из уравнения (2.10) – токи в ветвях схемы. Матрица напряжений на ветвях схемы
é & ù |
может быть определена из уравнения (1.8). Матрица узловых напряже- |
ëUв û |
é & |
ù |
определяется в данном случае по выражению: |
|
|||||||
ний ëUD û |
|
|||||||||
|
|
é & |
ù |
= |
é |
-1 |
ù é & |
ù |
é & |
ù |
|
|
ëUD û |
ëMat |
û ëUВa û |
= [C0t ]ëUВa û . |
|||||
Последнее уравнение получено из соотношения(2.4) при его на блоки, соответствующие дереву и хордам схемы:
(2.15)
разделении
|
éUВa ù |
éMat ù |
|
|||
é & ù |
& |
|
|
|
|
é & ù |
= ê & |
ú |
= ê |
|
ú |
||
ëUВ û |
Mbt |
ëUD û . |
||||
|
êUВb ú |
ë |
û |
|
||
|
ë |
û |
|
|
||
Отсюда получается:
é |
& |
ù |
|
é |
& |
ù |
ëUВa û |
= [Mat ]ëUD û, |
|||||
éU ù |
= éM |
ù éU ù. |
||||
ë |
& |
Вb û |
ë |
bt û ë |
& |
D û |
|
|
|||||
(2.16)
(2.17)
Так как матрица [Mat ] является квадратной и неособенной, то уравне-
ние (2.16) может быть разрешено относительно узловых напряжений, что и сделано в уравнении (2.15). Следовательно, достаточно знать напряжения на ветвях дерева схемы, чтобы определить напряжения всех узлов схемы относительно базисного узла.
2.4. Расчет режима сети, содержащей источники тока и напряжения.
Определение параметров режима сети в данном случае может быть произведено методом контурных токов. В качестве искомых неизвестных
34
при этом выбираются контурные токи. Их число равно числу независимых контуров схемы.
При решении задачи распределение задающих токов J& по ветвям схемы выбирается произвольным, но таким образом, чтобы оно удовлетворяло первому закону Кирхгофа. Второй закон Кирхгофа при таком распределении задающих токов, как правило, не выполняется, т.е. возникает небаланс напряжений по независимым контурам схемы. Небаланс напряжений устраняется с помощью контурных токов, величина которых определяется как небалансом напряжений, возникшим вследствие произвольного распределения задающих токов, так и контурными э.д.с.
Ток в каждой ветви и соответственно матрицу токов в ветвях схемы можно представить состоящими из двух слагаемых:
é&ù |
é&¢ù |
é&¢¢ù |
(2.18) |
|
ëIû =ëI û |
+ ëI û. |
|||
|
|
|
é&ù |
и соответствует |
Первое слагаемое связано с задающими токамиëJû |
||||
первому закону Кирхгофа |
|
|
|
|
|
é&¢ù |
é& |
ù |
(2.19) |
[M]ëI û |
=ëJ |
û. |
||
Второе слагаемое связано с контурными токами, и его величина может |
||||
быть определена в соответствии с (2.10) из выражения |
|
|||
é&¢¢ù |
|
é& |
ù |
(2.20) |
ëI û |
=[Nt ]ëIк û. |
|||
Так как контурные токи не связаны непосредственно с задающими то- |
||||
ками схему, то слагаемое |
é&¢¢ù |
тоже удовлетворяет первому закону Кирхгофа |
||
ëI û |
||||
|
[M]ëéI¢¢ûù =[M][Nt ]ëéIк ûù |
=[0 |
]. |
|
|
& |
& |
|
|
Для упрощения решения предполагают, что хорды отсутствуют. При этом считается, что задающие токи распределяются только по ветвям дерева схемы. В этом случае матрица токов в ветвях дерева схемы, вызванных задающими токами, может быть определена из уравнения (2.1):
é&¢ ù |
é&ù |
, |
ëIa û |
=[C0 ]ëJû |
а матрица токов в хордах схемы в соответствии с принятым выше предположением равна нулевой.
Таким образом, матрица |
é&¢ù |
может быть определена непосредственно |
||||
ëI |
û |
|||||
из следующего уравнения: |
|
|
éC0 ù |
|
|
|
|
é&¢ù |
é&ù |
(2.21) |
|||
|
ëI û |
=ê |
ú |
ëJû. |
||
|
|
|
ë |
0 û |
|
|
Действительные токи в ветвях получаются только после суммирования |
||||||
&¢ |
& |
. Из (2.18), (2.20) и (2.21) следует, что мат- |
||||
токов I с контурными токами Iк |
||||||
é&ù |
|
|
|
|
|
|
рица токов ëIû должна иметь следующий вид: |
|
|||||
é&ù |
éC0 ù |
é&ù |
|
é& ù |
(2.22) |
|
ëIû = |
ê |
ú |
ëJû |
+[Nt ë]Iк û |
||
|
ë 0 |
û |
|
|
|
|
35
или, после разделения на блоки,
éI |
|
ù |
éC |
|
ù |
|
éN |
|
ù |
|
|||
ê |
& |
a |
ú=ê |
|
0 |
|
é&ù |
+ ê |
|
at |
|
é& ù |
|
|
|
ú |
|
ú |
|||||||||
& |
0 |
ëJû |
Nbt |
ëIк û. |
|||||||||
êIb |
ú |
ë |
û |
|
ë |
û |
|
||||||
ë |
|
|
û |
|
|
|
|
|
|
|
|
||
Полученное обобщенное уравнение разделяется на два:
é |
& ù |
|
|
é&ù |
é& |
ù |
, |
ëIa û |
=[C0 ]ëJû |
+[Nat ]ëIк û |
|||||
é |
& ù |
= |
é |
ù é& |
ù |
|
(2.23) |
|
|
||||||
ëIb û |
ëNbt û ëIк û. |
|
|
||||
Если принять (как это было рекомендовано выше), что каждая хорда входит только в один контур, то
éëNb ûù=éëNbt ùû =[1 ]
и, следовательно,
é& ù |
é& ù |
, |
(2.24) |
ëIb û |
= ëIк û |
то ecть токи в хордах равны соответствующим контурным токам.
Для определения матрицы контурных токов необходимо применить второе уравнение состояния. Из (1.16) и (2.22) получается:
[ |
N |
éZ& |
ù éI&ù |
= |
[ |
N |
éZ& |
ù |
æ |
[ |
N |
t |
|
|
]ë |
В û ë û |
|
|
]ë |
В û |
ç |
|
|||||
|
|
|
|
[ |
|
]ë |
В û[ |
è |
|
t ] |
|
||
|
|
|
|
|
|
|
|
||||||
Произведение |
|
|
|
|
& |
ù N |
|
|
|||||
|
N éZ |
|
|
||||||||||
é& ù |
éC0 ù |
é&ù |
ö |
= |
é & ù |
é & ù |
|
ë]Ik û |
+ ê |
ú |
ëJû |
÷ |
[N ]ëEû |
= ëEk û . |
|
|
ë |
0 û |
|
ø |
|
|
|
дает |
квадратную |
неособенную матрицу |
|||||
порядка к . Поэтому из последнего уравнения можно определить матрицу контурных токов
& |
|
|
|
[ |
|
] |
& |
|
[ |
|
|
-1 |
æ |
[ |
|
] |
& |
|
[ |
|
] |
& |
|
éC0 ù |
& ö |
|
|||
éI |
ù |
= |
|
N |
|
ù |
N |
] |
|
N |
|
- |
N |
|
ù |
|
|
|
éJù |
|
. |
||||||||
( |
|
éZ |
|
t ) |
|
ç |
|
éEù |
|
éZ |
ê |
|
ú |
÷ |
|||||||||||||||
ë |
k û |
|
|
|
ë |
|
В û |
|
|
|
|
|
ë û |
|
|
|
ë |
|
В û |
0 |
ë û |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
ë |
û |
|
ø |
|
|
В более общем виде это уравнение имеет следующий вид:
|
|
|
|
|
é& |
ù |
= |
é & |
|
ù |
é& |
ù é & |
|
ù |
é & ù |
, |
|
|
|
|
|
|
|||||||||
где |
|
|
|
|
ëIк û |
ëСк |
û |
ëJ |
û |
+ |
ëУh û |
ëEû |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
éC0 ù |
|||
|
& |
|
|
|
|
|
|
[ |
|
] |
& |
|
[ |
|
|
|
|
-1 |
[ |
] |
|
& |
|
|
|||||||
éC |
|
ù |
= - |
( |
|
N éZ |
ù |
|
N |
t ) |
|
|
|
N éZ |
|
ù |
ê |
ú |
|||||||||||||
ë |
|
|
k û |
|
|
|
|
ë |
|
|
В û |
|
|
|
|
|
|
ë |
|
В û |
|||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
0 û |
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
||
é |
& |
ù = |
|
|
|
|
|
& |
|
|
ù[N |
|
|
× [N ]= |
é |
& |
|
|
ù[N ]. |
||||||||||||
У |
[N ]éZ |
|
t |
] |
|
У |
|
||||||||||||||||||||||||
ë |
|
|
h û |
|
|
|
|
ë |
|
|
В û |
|
|
) |
|
|
|
|
|
|
|
ë |
|
|
k û |
||||||
(2.25)
(2.26)
(2.27)
Уравнением (2.25) формируется принцип наложения применительно к контурным токам. При принятых условиях матрица контурных токов представляется в виде двух слагаемых, определяемых матрицами параметров
é & ù |
é & |
ù |
ëСк û |
и ëУк û . |
|
|
é & ù |
- матрица своеобразных (условных) коэффициентов распределе- |
|
ëСк û |
|
ния токов. При выбранном распределении задающих токов по ветвям дерева коэффициенты этой матрицы определяют контурные токи, устраняющие небаланс напряжений в независимых контурах схемы.
36
é & ù |
- матрица проводимостей, связываюшая э.д.с. ветвей с контур- |
ëУк û |
ными токами.
Описанный выше путь расчета токов в ветвях схемы является достаточно рациональным, т.к. требует определения обратной матрицы порядка к. Этот путь расчета может быть применен также и в том случае, когда схема содержит активные параметры только в виде задающих токов.
Таким образом, в рассматриваемом случае при расчете режима сети вначале из уравнения (2.25) определяются контурные токи, а затем из уравнений (2.23) и (2.24) - токи в ветвях схемы. Матрица напряжений на ветвях
схемы |
é & |
ù |
|
|
ëUВ |
ûможет быть определена из уравнения(1.8), а матрица узловых |
|||
напряжений |
é & |
ù |
- из уравнения (2.15). |
|
ëUD û |
||||
2.5. Метод последовательного исключения (метод Гаусса).
Метод последовательного исключения (метод Гаусса) – один из наиболее распространенных методов решения систем линейных алгебраических уравнений. Если точно выполнить все действия по методу Гаусса, то получим точное решение системы. Вычислительные схемы, с помощью которых может быть реализован метод Гаусса, различны. Рассмотрим одну из них– схему единственного деления. Запишем систему трех уравнений с тремя неизвестными.
а11х1 +а12х2 +а13х3 =а14 ; üï а21х1 +а22х2 +а23х3 =а24 ;ý (2.28)
а31х1 +а32х2 +а33х3 =а34 . ïþ
Пусть а11 ¹0 - “ведущий элемент”. Разделим первое уравнение системы (2.28) на а11 и получим:
х1 +b12х2 +b13х3 =b14 , |
(2.29) |
|||
где |
|
a1j |
|
|
b |
= |
( j = 2, 3, 4) . |
|
|
|
|
|||
1j |
|
a11 |
|
|
|
|
|
|
|
Теперь, пользуясь уравнением (2.29), можно исключить неизвестное х1 из второго и третьего уравнений системы(2.28). Для этого исключения нужно умножить уравнение (2.29) на а21 и а31 и вычесть результаты соответственно из второго и третьего уравнений системы(2.28). В результате получим систему двух уравнений с двумя неизвестными:
37
а |
(1) |
х2 |
+а |
(1) |
х3 |
=а |
(1) |
ü |
|
||
22 |
23 |
24 |
;ï |
(2.30) |
|||||||
|
(1) |
|
|
|
(1) |
|
|
|
(1) |
ý |
|
а |
х |
2 |
+а |
х |
3 |
=а |
,ï |
|
|||
|
32 |
|
|
33 |
|
|
34 |
þ |
|
||
где коэффициенты а(1) вычисляются по формуле |
|
|
|
|||||||||||||||||
|
|
|
kj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а(1) |
=а |
kj |
-а |
kj |
b |
(k=2,3; j=2,3, 4). |
(2.31) |
||||||||||
|
|
|
kj |
|
|
|
1j |
|
|
|
|
|
|
|
|
|||||
Из системы (2.30) можно так же исключить переменнуюх2 , как ис- |
||||||||||||||||||||
ключили |
х1 из системы (2.28). Для |
этого |
разделим коэффициенты первого |
|||||||||||||||||
уравнения системы (2.30) на “ведущий элемент” а(1) |
и получим: |
|
||||||||||||||||||
|
|
|
|
|
|
|
х2 +b23(1) х3 =b(1)24 , |
22 |
|
|
||||||||||
|
|
(1) |
|
|
|
|
|
|
(2.32) |
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где b(1) = |
|
2 j |
( j= 3, 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 j |
a |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем умножим (2.32) на а32(1) |
и вычтем результат из второго уравнения |
|||||||||||||||||||
системы (2.30). При этом получим уравнение |
|
|
|
|||||||||||||||||
где |
|
|
|
|
|
|
|
а33(2) х3 =а34(2) , |
|
|
(2.33) |
|||||||||
|
|
а(2) |
|
|
(1) -а |
(1) b(1) |
|
|
|
|
|
|
||||||||
|
|
|
= а |
( j=3, 4). |
|
(2.34) |
||||||||||||||
|
|
|
|
3 j |
|
|
|
3 j |
|
|
32 |
2 j |
|
|
|
|
|
|
||
Таким образом, система (2.28) приведена к эквивалентной системе |
||||||||||||||||||||
треугольного вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
х +b x |
2 |
+ b x |
3 |
= b ;ü |
|
|
|||||||||||
|
|
|
|
1 |
|
|
12 |
|
|
|
13 |
|
|
14 |
ï |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
(1) |
ï |
|
(2.35) |
|
|
|
|
|
|
|
|
|
х2 + b23 x3 |
=b24 |
;ý |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
а(2) х |
|
|
|
|
ï |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
=а(2) . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
3 |
|
34 |
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ |
|
|
||||
Из |
системы (2.35) последовательно |
|
найдем |
значения всех |
трех неиз- |
|||||||||||||||
вестных: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х3 = |
|
34 |
; |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
а |
(2) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
х2 =b(1)24 -b(1)23 x3 ; |
|
|
(2.36) |
||||||||||
|
|
|
х1 =b14 -b13 x3 -b12 x2 . |
|
|
|
||||||||||||||
Решение по методу Гаусса распадается на два этапа: прямой ход - приведение системы (2.28) к эквивалентной системе (2.35) с треугольной матрицей и обратный ход – вычисление неизвестных в соответствии с (2.36).
При расчете установившегося режима матрица узловых проводимостей или контурных сопротивлений является симметрической. Соответственно
38
матрицы систем, вычисляемых по методу Гаусса [например, система (2.30)], также симметрические. Это обстоятельство можно использовать для экономии памяти ЭВМ.
Общее количество арифметических действий по методу Гауссане
сколько меньше n3 , где n – число неизвестных. Машинное время, необходимое для выполнения арифметических операций по методу Гаусса, пропорционально кубу числа неизвестных.
Достоинство метода Гаусса состоит в том, что его применение гарантирует получение решения в результате выполнения определенного числа арифметических операций, причем число необходимых операций определяется только порядком системы n. В этом состоит преимущество метода Гаус-
са и других точных методов перед приближенными, или итерационными, для которых число необходимых арифметических вычислений зависит не только от порядка системы, но и от заранее неизвестного количества шагов, за которые сойдется итерационный процесс.
Недостаток метода Гаусса состоит в необходимости запоминать матрицу элементов системы уравнений. Для расчета сложных электрических систем эффективное применение метода Гаусса невозможно без использования специальных методов, учитывающих слабую заполненность матрицы узловых проводимостей и контурных сопротивлений. К сожалению, такой учет алгоритмически достаточно сложен и, кроме того, его применение неполностью устраняет недостатки метода Гаусса, связанные с необходимостью использования большой памяти ЭВМ в расчетах режимов сложных электрических систем.
2.6. Простая итерация.
Точные методы решения системы линейных уравнений установившегося режима сложных электрических систем с большим числом неизвестных могут оказаться труднореализуемыми. В расчетах режимов сложных электрических систем метод исключения Гаусса и тем более применение обратной матрицы могут привести к необходимости использования большого объема памяти ЭВМ или недопустимой длительности расчетов.
В этих условиях для расчета установившегося режима иногда удобнее использовать приближенные или итерационные методы. Часто эти методы называют методами последовательных приближений. Для понимания их сути рассмотрим простейший из этих методов — простую итерацию.
Для определенности вначале ограничимся рассмотренной выше системой уравнений третьего порядка (2.28).
Предполагая, что диагональные коэффициенты aii ¹0, i =1, 2,3, разрешим первое уравнение системы (2.28) относительно х1, второе - относительно х 2 , а третье - относительно х3 . Тогда получим систему, эквивалентную
(2.28):
39
x = |
|
b x |
2 |
+ b x |
3 |
+ b ; |
ü |
|
||||||
1 |
=b21x1 |
12 |
|
13 |
1 |
|
ï |
(2.37) |
||||||
x2 |
|
|
|
|
+ b23x3 +b2 ;ý |
|||||||||
x |
3 |
=b x + b |
32 |
x |
2 |
|
+b |
3 |
, |
ï |
|
|||
|
31 |
1 |
|
|
|
|
|
|
þ |
|
||||
где
bkj =- |
akj |
при k¹ j ; bk =- |
a |
k4 |
, |
k=1, 2,3 ; |
i =1, 2,3; |
aii |
|
|
|||||
|
|
aii |
|
|
|||
|
|
j = 1, 2,3. |
|
(2.38) |
|||
Зададим начальные значения неизвестныхх1(0), х1(0), х1(0), исходя из физического смысла решаемой задачи. Подставляя эти значения в правые ча-
сти системы (2.37) , получаем первые приближения х1(1) , х(1)2 , х(1)3 . Вычисле-
ние первого приближения неизвестных соответствует первому шагу итерационного процесса. Полученные первые приближения могут быть таким же образом использованы для получения вторых, третьих и т.д. Приближения неизвестных на (i +1)-й итерации можно получить, используя значения переменных на предыдущем i-м шаге:
|
|
|
x |
(i+1) = |
|
|
|
|
b x |
(i) +b x(i) +b ; |
ü |
|
||||||||||
|
|
|
1 |
|
|
|
|
(i ) |
|
12 |
|
2 |
|
13 |
3 |
1 |
|
ï |
|
|||
|
|
|
x |
(i+1 ) |
|
|
|
|
|
|
|
|
|
|
|
(i ) |
|
|
ï |
(2.39) |
||
|
|
|
2 |
=b21x1 |
|
|
|
|
+ b23x3 |
+b2 ;ý |
||||||||||||
|
|
|
x |
(i+1 )=b x |
(i ) |
+ b |
|
x(i ) |
|
|
|
|
+b |
|
ï |
|
||||||
|
|
|
32 |
|
|
|
|
3 |
,ï |
|
||||||||||||
|
|
|
|
3 |
|
31 |
1 |
|
|
|
2 |
|
|
|
|
|
þ |
|
||||
Введем матрицу и вектор-столбцы |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
éb11 |
b12 |
b13 |
ù |
|
|
|
|
éх1 |
ù |
|
|
éb1 ù |
|
|||||||
[ |
B = |
êb |
21 |
b |
22 |
b |
|
|
ú, |
[ |
C = êх |
|
ú, |
[ |
b = êb |
ú. |
|
|||||
] |
ê |
|
|
23 ú |
|
] |
ê |
2 ú |
] |
ê |
|
2 ú |
|
|||||||||
|
|
ê |
|
b32 |
|
|
|
ú |
|
|
|
|
ê |
|
ú |
|
|
ê |
|
ú |
|
|
|
|
ëb31 |
b33 û |
|
|
|
|
ëх3 |
û |
|
|
ëb3 û |
|
|||||||||
Диагональные элементы матрицы В равны нулю, т.е. bkk = 0, а недиа- |
||||||||||||||||||||||
гональные элементы, т.е. bkj |
совпадают с коэффициентами систем (2.37) или |
|||||||||||||||||||||
(2.39). Учитывая правило умножения и сложения матриц, систему (2.37) можно записать в матричной форме:
[C] = [B][C]+[b]. |
|
(2.40) |
|
Итерационное выражение (2.39) можно записать в матричном виде: |
|||
éCi+1ù = [B |
]éCi ù +[b ]. |
(2.41) |
|
ë |
û |
ë û |
|
Итерационный процесс, определяемый выражением |
(2.39) или (2.41), |
||
называется простой итерацией. Итерационные методы дают возможность по-
40
лучить последовательность приближенных значений неизвестных, сходящуюся к точному решению системы. Если элементы матрицы [B] удовлетворяют определенным условиям, то процесс простой итерации сходится к точно-
é % ù |
|
|
|
|
é |
(0 )ù |
му решению системы ëCû при любом начальном значенииëC |
û . Сходи- |
|||||
мость к решению означает, что |
|
|
|
|
|
|
lim éC(i )ù |
= éC% |
ù. |
|
|
|
(2.42) |
i®¥ ë û |
ë |
û |
|
|
|
|
Таким образом, точное решение получается лишь в результате беско- |
||||||
нечного итерационного процесса. Всякий вектор |
é |
(i) ù |
, определяемый на i-м |
|||
êC |
ú |
|||||
|
|
|
ë |
û |
|
|
шаге, является приближенным решением системы(2.28). Вектор погрешности этого приближенного решения равен:
|
|
é |
е |
(i) ù |
|
é % ù |
é |
C |
(i) ù |
. |
(2.43) |
||||||
|
|
ê |
|
ú |
= ëCû- |
ê |
|
ú |
|||||||||
|
|
ë |
|
|
|
û |
|
|
|
ë |
|
|
|
û |
|
|
|
В практических расчетах точное решение системы неизвестно, и о по- |
|||||||||||||||||
грешности решения судят не по |
é |
|
|
(i) ù |
а по разности между значениями пе- |
||||||||||||
êе |
ú |
||||||||||||||||
|
|
ë |
|
|
û |
|
|
|
|
|
|
|
|
|
|
||
ременных на i-м и (i+1)-м шагах, т.е. по вектору поправок: |
|
||||||||||||||||
é |
|
|
(i) ù é |
(i+1) ù é |
|
|
(i) ù |
(2.44) |
|||||||||
|
êDC |
|
|
ú |
= |
êC |
|
ú |
- êC |
ú. |
|||||||
ë |
|
|
|
|
û |
|
ë |
|
û |
|
ë |
|
|
û |
|
||
Часто считают, что итерационный процесс сошелся, если поправки для |
|||||||||||||||||
всех переменных меньше наперед заданной величины e , т.е. при |
|
||||||||||||||||
|
Dх(ki) |
|
<e, |
k=1,..., n . |
|
|
|
(2.45) |
|||||||||
|
|
|
|
|
|||||||||||||
где n — порядок решаемой системы.
Если простая итерация сходится быстро, т.е. если для решения системы n-го порядка требуется менееn шагов, то при расчете на ЭВМ получим выигрыш во времени по сравнению с точными методами, например с методом Гаусса. Это вытекает из того, что число арифметических операций, необхо-
димых для одного шага простой итерации, пропорционально n2 , а общее число арифметических операций, например по методу Гаусса, примерно про-
порционально n3 . Приведенное соотношение числа операций справедливо для расчетов установившегося режима, если не учитывается слабая заполненность матрицы узловых проводимостей или контурных сопротивлений. В то же время и в случае учета слабой заполненности этих матриц простая итерация если и сходится быстро, то требует меньше времени ЭВМ, чем точные методы.
2.7. Метод Зейделя.
Значительно большее распространение, чем метод простой итерации, получил метод Зейделя, который, как правило, отличается более быстрой сходимостью. Метод Зейделя представляет собой незначительную модифи-
41
кацию простой итерации. Основная его идея заключается в том, что найден-
(i+1)
ное (i+1)-е приближение (к-1)-го неизвестного xk-1 сразу же используется
для вычисления следующего к-го неизвестного x(ki+1) . Иными словами, полученное (i+1)-е значение переменной x1 сразу же используется для вычисления (i+1)-гo значения переменных x2 , x3 и т.д. Таким образом, для системы (2.28) итерационный процесс метода Зейделя описывается следующими выражениями:
x |
(i+1) |
= |
|
b x(i) |
+ b x(i) |
+b ; |
ü |
|
||||||
1 |
|
(i+1 ) |
12 |
|
2 |
13 |
3 |
|
1 |
|
ï |
|
||
x |
(i+1 ) |
|
|
|
|
|
(i ) |
|
|
ï |
(2.46) |
|||
2 |
=b21x1 |
|
|
|
|
+ b23x3 |
|
+b2 ; ý |
||||||
x |
(i+1 )=b x(i+1 )+b |
|
x |
(i+1 ) |
|
|
+b |
|
ï |
|
||||
32 |
|
|
3 |
,ï |
|
|||||||||
|
3 |
31 |
1 |
|
|
2 |
|
|
|
|
þ |
|
||
По методу простой итерации(i+1)-е приближение к-й переменной x(ki+1) для системы порядка n вычисляется по следующему выражению:
(i+1 ) |
k-1 |
(i ) |
n |
(i ) |
+bk . |
(2.47) |
|
xk |
= å bkj x j |
+ å bkj x j |
|||||
|
|
j=1 |
|
j=k+1 |
|
|
|
По методу Зейделя (i+1)-е приближение к-й переменной x(ki+1) вычисляется так:
(i+1 ) |
k-1 |
(i+1 ) |
n |
(i ) |
+ bk . |
(2.48) |
||
xk |
= å bkj x j |
+ |
å bkj x j |
|||||
|
|
j=1 |
|
|
j=k+1 |
|
|
|
Как правило, метод Зейделя надежнее и быстрее сходится, чем метод простой итерации. Более надежная сходимость означает, что метод Зейделя сходится в тех случаях, когда сходится простая итерация, и может сходится, когда простая итерация расходится.
Алгоритмическая реализация метода Зейделя столь же проста, как и простой итерации. Единственное изменение в алгоритме расчета состоит в
засылке вычисленного U(ki+1) в то место памяти, где ранее хранилось U(ki) . В сравнении с точными методами быстро сходящийся процесс Зейделя при сходимости за число шагов, меньшее n, обладает теми же преимуществами с точки зрения времени расчета, что и простая итерация.
Поскольку метод простой итерации не имеет никаких преимуществ перед методом Зейделя, в практических расчетах установившихся режимов в электрических системах на ЭВМ всегда используется метод Зейделя, а не простая итерация.
В то же время отметим, что рассмотрение простой итерации важно для понимания сути применения итерационных методов расчета установившихся режимов электрических систем.
Указанные выше преимущества метода Зейделя и простой итерации с точки зрения памяти и времени расчета относятся только к случаю быстрой
42
сходимости итерационных процессов. Во многих случаях в расчетах сложных электрических систем метод Зейделя сходится медленно. Поэтому для эффективного применения метода Зейделя в расчете установившихся режимов сложных электрических систем необходимо ускорение сходимости с помощью ускоряющих коэффициентов.
2.8. Методы решения нелинейных уравнений установившегося режима.
Электрическая система характеризуется особенностями, отличающими ее от других видов электрических цепей. Сети современных электрических систем обычно трехфазные. Будем рассматривать расчеты симметричных установившихся режимов, при которых используется расчетная схема одной фазы.
Все пассивные элементы электрических систем будем предполагать линейными. Пассивные элементы электрической системы - это воздушные и кабельные линии электропередачи, трансформаторы и автотрансформаторы, установленные на подстанциях, а также реакторы и устройства продольной или поперечной компенсации реактивной мощности.
Активные элементы в электрических системахэто источники тока, соответствующие нагрузкам потребителей и генераторов электрических станций. В расчетах установившихся режимов электрических систем во многих случаях учитываются нелинейные характеристики источников тока. Рас-
смотрим возможные способы задания нагрузок потребителей в расчетах установившихся режимов сложных электрических систем.
Нагрузки потребителей представляются следующим образом.
1. Статические характеристики, т.е зависимости активной и реактивной мощностей нагрузки от напряжения Rн (U), Qн (U). Статическая характери-
стика для каждой нагрузки определяется составом потребителей. В большинстве случаев используют типовые статические характеристики для некоторой условной комбинированной по составу нагрузки. Такой способ задания нагрузки потребителей следует считать наиболее точным.
2. Мощности, постоянные по величине, Rн =co nst , Qн =const . Этот способ задания нагрузки является точным для электрических систем, полностью обеспеченных устройствами регулирования напряжения. В этих системах на электроприемниках поддерживается постоянное напряжение вследствие широкого использования трансформаторов и автотрансформаторов с регулированием напряжения под нагрузкой, а также за счет оснащения нерегулируемых трансформаторов на существующих подстанциях линейными регуляторами регулировочных автотрансформаторов или вольтодобавочными трансформаторами. Кроме того, широко используются средства местного регулирования напряжения (управляемые батареи конденсаторов, синхронные двигатели и т..)д. В действительности у потребителей не обес-
43
печивается постоянство напряжения. В этом случае задание постоянной мощности нагрузки потребителей приводит к ошибкам в расчетах установившихся режимов. Величина этой ошибки тем больше, чем больше отличаются напряжения потребителей от номинального.
Введение балансирующего узла – это допущение, вызванное особенностью нелинейных уравнений установившегося режима. Эта особенность заключается в том, что невозможно точно задать мощности во всех узлах, удовлетворяющие условию баланса в системе, т.к. потери мощности не могут быть точно определены до расчета установившегося режима. В этом одно из отличий от линейных уравнений, где использование балансирующего узла – не допущение и его выбор не влияет на результат расчета.
Нелинейные уравнения узловых напряжений описывают установившийся режим электрической системы при задании нелинейных источников тока. Таким образом, генераторы с постоянной мощностью либо нагрузки потребителей, заданные статистической характеристикой или постоянной мощностью, соответствуют нелинейным источникам тока в схеме замещения электрической системы. Постоянная мощность нагрузки потребителя или генератора задается в виде узлового тока
|
|
|
|
& |
|
|
& |
k ( |
& |
) |
Sk |
|
|
* |
|
|
||||
I |
|
U |
= |
Uk |
, |
(2.49) |
|
|
|
|
|
* |
|
& |
|
|
|
|
|
|
|
|
|
|
го узла; |
Uk - сопряженный ком- |
|
где Sk = const - постоянная мощность k - |
||||||
плекс напряжения k - го узла; &Ik (U& ) - нелинейный источник тока, зависящий
от напряжения.
Если мощность нагрузки потребителя задана статистической характеристикой, то нелинейный источник тока определяется следующим выражением:
|
|
|
|
& |
& |
|
& |
& |
& |
|
|
& |
k ( |
& |
) |
Sk (U) |
|
Rk (U)- jQk (U) |
|
|
|||
I |
|
|
* |
= |
|
|
* |
, |
(2.50) |
||
|
U = |
|
|
|
|
|
|||||
|
|
|
|
|
Uk |
|
|
|
Uk |
|
|
где R& k (U& ),Qk (U& ) - статистические характеристики активной и реактивной
нагрузок k - го узла. |
|
|
|
|
|
|
|
||
де: |
Уравнения узловых напряжений (2.6) можно записать в следующем ви- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
é&ù |
é ù é & |
ù |
é ù |
é & |
ù é & ù |
(2.51) |
|
|
|
ëJû= |
ëYу û ëUD û= |
ëYу û(ëU |
û- |
ëUб û). |
|||
Здесь |
é & ù |
- матрица напряжений в узлах; |
é & |
ù |
- матрица напряжений в ба- |
||||
ëUû |
ëUd û |
||||||||
лансирующем узле.
Для системы переменного тока из четырех узлов уравнение(2.51) примет вид:
44
|
& |
|
& |
|
& |
& |
|
& |
& |
& |
; |
ü |
|
у11 (U1 |
-Uб )- у12 (U2 |
-Uб )- у13 |
(U3 |
-Uб )=J1 |
ï |
|
|||||||
& |
|
|
|
& |
|
|
& |
|
|
|
|
|
|
|
& |
|
& |
|
& |
& |
|
& |
& |
& |
|
ï |
(2.52) |
- у21 (U1 |
- Uб )+ у22 |
(U2 |
-Uб )- у23 |
(U3 |
- Uб )=J2 ;ý |
||||||||
& |
|
|
|
|
|
|
& |
|
|
|
|
ï |
|
|
& |
|
& |
|
& |
& |
|
& |
& |
& |
|
|
|
|
|
|
|
. ï |
|
||||||||
- у31 (U1 |
-Uб )- у32 |
(U2 |
- Uб )- у33 |
(U3 |
- Uб )=J3 |
|
|||||||
& |
|
|
|
& |
|
|
& |
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим
у&1б = у&11 -у&12 -у&13 ; у&2б = у& 22 - у& 21 -у&23 ; у&3б = у&33 - у&31 - у&32 .
С учетом принятых обозначений уравнения (2.52) примут вид:
& |
& |
& |
& |
& |
& |
& |
|
& |
& |
ü |
|
у11 U1 |
- у12 |
U2 |
- у13 U3 |
=J1 |
+ у1б |
Uб ; |
ï |
|
|||
|
& |
|
& |
- у |
& |
& |
|
|
& |
; ý |
(2.53) |
- у21 U1 |
+ у22 U2 |
23 U3 |
=J2 |
+ у2б Uб |
|||||||
& |
|
|
|
& |
|
|
|
& |
|
ï |
|
|
& |
|
& |
|
& |
& |
|
|
& |
|
|
- у31 U1 |
- у32 U2 |
- у33 U3 |
=J3 |
+ у3б Uб |
.þ |
|
|||||
& |
|
& |
|
& |
|
|
|
& |
|
|
|
Если постоянная мощность нагрузки потребителя или генератора задается в виде узлового тока (2.49), то система (2.53) окончательно примет вид:
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
ü |
|
|
& |
& |
& |
& |
& |
& |
= |
|
S1 |
|
|
& |
& |
ï |
|
||
|
* |
|
|
|||||||||||||
у11 U1 |
- у12 |
U2 |
-у13 U3 |
|
|
|
+ у1б |
Uб ; |
ï |
|
||||||
|
|
|
|
|
|
|
U1 |
|
|
|
ï |
|
||||
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
ï |
|
|
|
& |
|
& |
|
& |
|
S2 |
|
|
|
& |
ï |
|
|||
- у21 U1 |
+ у22 U2 |
- у23 U3 |
= |
|
* |
|
|
|
+ у2б Uб |
;ý |
(2.54) |
|||||
& |
|
|
|
& |
|
|
|
|
|
|
|
|
& |
|
ï |
|
|
|
|
|
|
|
|
U2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ï |
|
|||||
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
||
|
& |
|
& |
|
& |
|
|
|
S3 |
|
|
& |
ï |
|
||
- у31 U1 |
- у32 U2 |
- у33 U3 |
= |
|
* |
|
|
|
+ у3б Uб |
.ï |
|
|||||
& |
|
& |
|
& |
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
U3 |
|
|
þï |
|
|||
Уравнения (2.54) являются нелинейными узловыми уравнениями. Методы решения этих уравнений– приближенные или итерационные. Точных методов, пригодных для решения нелинейных алгебраических уравнений, не существует.
Система нелинейных уравнений узловых напряжений в форме баланса токов обладает следующей особенностью. Эта система уравнений «линейна слева» и нелинейна в правой части. Сравним линейные уравнения узловых напряжений (2.52) и нелинейные (2.54). Левые части их одинаковы и равны произведению матрицы проводимостей узлов на вектор-столбец переменных - напряжений узлов. Именно в этом смысле нелинейная система уравнений узловых напряжений в форме баланса токов«линейна слева». Нелинейность системы (2.54) состоит только в наличии нелинейных правых частей. Физически эта особенность определяется тем, что все параметры схемы замеще-
ния электрической системы линейны, кроме задающих токов J&k (U& ). Иногда
говорят, что продольная часть схемы замещения линейна, а поперечная - нелинейна.
45

Поскольку система уравнений узловых напряжений нелинейна лишь в правой части, для ее решения могут быть применены все рассмотренные в гл.II методы. При этом на каждом шаге итерационного процесса можно считать систему (2.54) линейной и использовать методы решения, описанные в данной главе.
В качестве примера рассмотрим применение метода Гаусса при расчете нелинейных узловых напряжений.
Метод Гаусса при расчете нелинейных уравнений узловых напряжений можно использовать на каждом шаге итерационного процесса, считая систему уравнений узловых напряжений линейной на данном шаге. Зададимся начальными приближениями узловых напряжений, т.е. зададимся начальным
приближением вектор-столбца переменных U& (0) . Определим правые части в нелинейной системе уравнений узловых напряжений в форме баланса токов
(2.54), т.е. вычислим элементы вектор-столбца при U& k = U& (k0) :
|
|
|
|
|
|
|
|
|
|
é |
|
|
& |
|
|
|
ù |
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
S1 |
|
& |
ú |
|
|
|
|
|
é |
|
|
|
(0 ) ù |
ê |
|
|
* (0 ) |
+ у1б Uб ú |
|
|||||
|
|
|
|
|
|
|
|
)ú |
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
& |
|
ê |
|
|
U1 |
|
|
ú |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ê I1 (U1 |
|
|
|
|
|
||||||||||
|
|
|
ê |
|
|
|
|
|
ú |
ê |
|
|
& |
|
|
|
ú |
|
|
|
(0 ) |
|
|
|
|
(0 ) |
|
ê |
|
|
S |
|
|
ú |
|
||
& |
)= |
ê |
|
|
& |
|
) |
ú |
|
|
|
2 |
|
|
& |
|
|
|
I (U |
ê I2 |
(U2 |
ú |
=ê * (0 ) |
+ у2б Uб ú . |
(2.55) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
ê |
|
|
& |
(0 ) |
ú |
ê U2 |
|
|
ú |
|
|||||
|
|
|
|
|
|
|
ú |
|
||||||||||
|
|
|
ê I3 |
(U3 |
) |
ú |
ê |
|
|
& |
|
|
|
|
||||
|
|
|
ë |
|
|
|
|
|
û |
ê |
|
|
S3 |
|
|
& |
ú |
|
|
|
|
|
|
|
|
|
|
|
ê |
* (0 ) |
|
+ у3б Uб ú |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
ë U3 |
|
|
û |
|
||||
Полагаем, что токи в узлах постоянны и определяются начальными приближениями узловых напряжений. Тогда уравнения узловых напряжений (2.54) превращаются в систему линейных алгебраических уравнений с правыми частями, вычисляемыми из (2.55):
|
& |
|
|
& |
|
& |
|
|
|
|
& (0) |
); |
|
|
|
|
|
|
|
|
|||||||
у11 U1 |
- у12 U2 |
- у13 U3 |
= I1 (U1 |
|
|||||||||
& |
|
|
& |
|
& |
|
|
|
|
|
|
|
|
|
& |
|
|
& |
|
& |
|
|
& (0 ) |
(2.56) |
|||
|
|
|
|
|
|||||||||
- у21 U1 |
+ у22 U2 |
- у23 U3 |
= I2 (U2 |
); |
|||||||||
& |
|
|
& |
|
& |
|
|
|
|
|
|
|
|
-у&31 U& 1 - у&32 U& 2 - у&33 U& 3 = I3 (U& (30 )).
Вматричной форме линейную систему(2.56) можно записать следующим образом:
|
|
|
é |
& |
ù é & (1)ù |
é |
|
& (0) |
ù |
(2.57) |
|
|
|
|
|
||||||||
|
|
|
ë |
Упр û êU |
ú |
= ê I (U |
)ú . |
||||
|
|
|
|
|
ë |
û |
ë |
|
|
û |
|
Решая систему (2.57), определяем первое приближение напряжений уз- |
|||||||||||
& (1) |
& (1) |
& (1) |
. Далее переходим ко второму шагу, |
т.е. определяем пра- |
|||||||
лов U1 |
, U2 |
, U3 |
|||||||||
46

вые части (2.55) при значениях узловых напряжений, равных их первым приближениям:
é |
|
& (1) ù |
é |
|
& |
(1) ù |
é& |
& |
ù |
|
|
||||||||
ê I (U )ú = |
ê I (U |
|
|
||||||
)ú + ëуkб Uб û. |
|||||||||
ë |
û |
ë |
|
|
û |
|
|
|
|
(2.58)
Затем найдем второе приближение узловых напряжений, решая линейную систему с той же матрицей Упр , и так далее до тех пор, пока процесс не
сойдется. При этом каждый шаг итерационного процесса состоит из опреде-
ления I (U& (i)) и решения системы линейных уравнений
é |
& |
ù é & (i+1)ù |
= |
é |
|
& (i) |
ù |
, |
(2.59) |
|
|
||||||||||
ë |
Упр û êU |
ú |
ê I (U |
)ú |
||||||
|
|
ë |
û |
|
ë |
|
|
û |
|
|
где i — номер шага.
3. Обращение матриц.
Как следует из приведенного выше материала, операция умножения на обратную матрицу может быть использована дня решения системы линейных алгебраических уравнений. При этом, независимо от технической сложности вычисления обратной матрицы, запись математических преобразований с ее использованием значительно упрощает решение многих задач. Ниже приводятся некоторые способы нахождения обратной матрицы.
3.1. Обращение матриц методом разделения на клетки.
Снижение порядка одновременно обращаемой матрицы можно получить разделением исходной матрицы на блоки. Если задана матрица [А]чет-
é& ù |
: |
ного порядка, то ее можно разделить на блоки вдвое меньшего порядка ëаij û |
|
|
|
é & ù |
éa11 |
a12 ù |
|
|
||||
|
|
|
ëΑû |
= ê |
& |
|
& |
ú . |
|
(3.1) |
|
|
|
|
|
21 |
|
|
|||||
|
|
|
|
|
ëa |
a22 û |
|
|
|||
|
|
|
|
|
|
& |
|
& |
|
|
|
|
|
Обратную матрицу |
также |
можно |
|
представить разделенной |
на блоки |
||||
& |
ù |
того же порядка: |
|
|
|
|
|
|
|
|
|
éb |
|
|
|
|
|
|
|
|
|
||
ë |
ij û |
|
|
|
|
|
|
|
|
|
|
|
|
é |
& -1 |
ù |
é & ù |
& |
|
& |
ù |
|
|
|
|
éb11 |
b12 |
(3.2) |
|||||||
|
|
ë |
Α |
û= |
ëΒû= ê& |
|
& |
ú . |
|||
|
|
|
|
|
|
|
ëb21 |
b22 |
û |
|
|
По определению произведение обратных матриц дает единичную мат-
рицу
47
é & ù é & ù éа11 |
а12 |
ù éb11 |
b12 ù é1 |
0ù |
|
|||||
ëΑû ëΒû |
= ê |
& |
|
& |
|
& |
& |
ú= ê |
ú. |
(3.3) |
|
|
ú ê& |
|
|||||||
|
21 |
а |
22 |
& |
||||||
|
ëа |
û ëb21 |
b22 |
û ë0 |
1û |
|
||||
|
|
& |
|
& |
|
|
|
|
|
|
Поле выполнения операции умножения получается следующая система матричных уравнений:
|
а& |
|
éb ù+ а& |
|
éb ù |
= 1 ; ü |
|
|||||||||||||
[ 11 ë] |
& |
û |
[ 12 |
ë] |
& |
û |
[ ] |
|
|
|||||||||||
|
11 |
|
21 |
ï |
|
|||||||||||||||
|
& |
|
é |
& |
ù |
|
|
& |
|
é |
& |
|
ù |
|
|
|
ï |
|
||
|
|
|
|
|
|
|
|
|
|
=[0 ];ï |
|
|||||||||
[а11 |
ë]b12 |
û |
+[а12 |
ë]b22 |
|
û |
(3.4) |
|||||||||||||
[ |
|
|
|
|
& |
ù |
|
[ |
|
|
|
|
& |
|
ù |
|
[ |
|
ý |
|
а& |
|
|
|
+ |
а& |
|
|
|
|
= |
0 ; |
|
||||||||
21 |
éb |
22 |
éb |
|
|
|||||||||||||||
|
ë] |
11 |
û |
|
|
ë] |
21 |
û |
|
] |
ï |
|
||||||||
[ |
а& |
|
|
|
& |
ù |
+ |
[ |
а& |
|
|
|
& |
|
ù |
= 1 . |
ï |
|
||
|
|
|
|
|
|
|
ï |
|
||||||||||||
21 |
éb |
22 |
éb |
|
|
|||||||||||||||
|
ë] |
12 |
û |
|
|
ë] |
22 û |
|
[ ] |
þ |
|
|||||||||
Если эту систему решать, пользуясь правилами матричной алгебры, то получаются следующие формулы для определения отдельных блоков матрицы [Β] :
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
-1 |
|
|
ù |
= |
|
а& |
|
|
- а& |
|
éа& |
ù |
[ |
а& |
|
)] |
; |
||||||||
éb |
|
|
|
|
|
21 |
|||||||||||||||||
ë |
11 |
û |
|
([ |
11 |
|
] [12 |
ë |
]22 |
û |
|
|
|
||||||||||
é |
& |
ù |
= - |
é |
& |
-1 |
ù |
& |
|
é& |
|
ù |
; |
|
|
|
|
||||||
ëb12 |
û |
ëа11 |
û[а12 |
ë]b22 |
û |
|
|
|
(3.5) |
||||||||||||||
é |
& |
ù |
= - |
é |
& |
-1 |
|
ù |
|
& |
|
|
é |
& |
ù |
; |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||||||
ëb21û |
ëа |
22 |
û |
[а21 ë]b11 |
û |
|
|
|
|
||||||||||||||
é |
& |
ù |
|
|
|
& |
|
|
|
é |
& |
-1 |
ù |
é |
& |
ù |
|
-1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ëb22 û |
= ([а21 |
|
ë]а11 |
û ëb12 û) . |
|
|
|||||||||||||||||
Полученные формулы показывают, что метод разделения исходной матрицы на блоки требует выполнения многих дополнительных операций и приводит к многократному обращению матрицы, хотя и вдвое меньшего порядка. Поэтому большого выигрыша в снижении трудоемкости вычисления обратной матрицы таким путем получить не удается. Однако техническое выполнение расчета при этом несколько облегчается.
Следует заметить, что непосредственное вычисление обратной матрицы рассмотренным методом, кроме громоздкости, имеет еще и другой существенный недостаток. Большое количество последовательно выполняемых
арифметических операций в случае матриц достаточно высокого порядка приводит к накоплению ошибки вычислений.
3.2. Итерационный метод.
Обычно матрицы параметров системы являются квадратными и симметричными. Во многих случаях их элементы, расположенные на главной диагонали, по модулю значительно больше остальных. Этим иногда можно пользоваться для приближенного определения обратной матрицы.
Имея такую матрицу, можно уточнить ее путем последовательных приближений (методом итераций). Однако при этом важно, чтобы приближенная
48
матрица все же была известна с достаточной точностью, т.е. чтобы элементы приближенной матрицы не сильно отличались от элементов точной матрицы.
Пусть, например, требуется определить обратную матрицу проводимостей ветвей [УВ ] .
é |
& -1 |
ù |
é & ù |
ë |
Ζв |
û |
= ëУв û . |
Приближенно эта матрица может быть определена при условии, что исходная
матрица |
é % ù |
имеет только одни диагональные элементы, а все остальные ее |
ëΖв û |
элементы равны нулю. Такая диагональная матрица получается из исходной
é |
& ù |
путем вычитания из нее матрицы |
é & |
|
ù |
, |
содержащей недиагональные |
|||||||||
ë |
Ζв û |
ëΖ |
û |
|||||||||||||
элементы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
é % |
ù |
é & |
ù |
é & |
ù |
. |
(3.6) |
|||||
Например, если |
|
ëΖв û |
= ëΖв û |
-ëΖD û |
||||||||||||
|
|
|
|
|
éΖ11 |
|
Ζ12 ù |
|
|
|
||||||
|
|
|
[ |
Ζ |
в |
= |
|
, |
|
|
||||||
|
|
|
|
] |
ê |
|
|
|
|
ú |
|
|
|
|||
|
|
|
|
|
|
|
|
ëΖ21 |
Ζ22 û |
|
|
|
||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é % |
ù |
= |
éΖ11 |
|
0 |
ù |
|
|
|
|||||
|
|
ëΖв û |
ê |
0 |
|
|
|
ú |
|
|
|
|||||
|
|
|
|
|
|
|
|
ë |
|
Ζ22 û |
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
Ζ |
|
= |
é |
0 |
|
Ζ12 |
ù . |
|
|
|
|||
|
|
|
|
|
] |
ê |
|
|
0 |
|
ú |
|
|
|
||
|
|
|
|
|
|
|
ëΖ21 |
|
|
û |
|
|
|
|||
Обратная диагональная матрица |
|
|
|
é % -1 |
|
|
|
|
|
|||||||
|
|
|
|
|
é % |
|
ù |
= |
ù |
|
|
|
(3.7) |
|||
|
|
|
|
|
ë |
Ув û |
ëΖв |
û |
|
|
|
|||||
определяется по указанному выше правилу и является приближенной обратной матрицей. Можно предположить, что действительная обратная матрица
é & ù |
получается из приближенной |
é % ù |
путем добавления к ней некоторой |
|||||
ëУв û |
ëУв û |
|||||||
|
é & |
ù |
: |
|
|
|
|
|
поправочной матрицы ëУD û |
|
|
|
+[У ] . |
|
|||
|
|
|
é |
& ù |
|
é % ù |
(3.8) |
|
|
|
|
ë |
Ув û |
= ëУв û |
|||
По определению |
|
|
|
|
|
|
|
|
|
=[1 ] |
é & |
ù é & |
ù |
é % |
ù |
é & |
|
ù é & ù |
|||
ëУв û ëΖв û |
=(ë |
Ув û |
+ ëУ |
û )ëΖв û |
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
é % |
|
ù é |
& ù é & |
ù é |
& |
ù |
(3.9) |
||
Отсюда следует, что |
ëУв |
û ëΖв û |
+ |
ëУ |
û ë |
Ζв û=[1] . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
é |
& |
ù é & |
ù |
|
é % |
ù é & ù |
|
||
|
ë |
У |
û ëΖв |
û |
= [1]- ë |
Ув û ëΖв û |
|
|||
49
или
é & |
ù |
= ([1 ]- |
é % ù é & ù é |
& -1 |
ù |
(3.10) |
ëУ |
û |
ëУв û ëΖв û )ë |
Ζв |
û. |
В первом приближении можно принять, что поправочная матрица достаточно точно определяется с помощью приближенной обратной матрицы:
|
|
é & |
ù |
|
é % ù é & |
ù |
é % ù |
|
|
|
(3.11) |
||
При этом |
|
ëУ |
û » |
([1]- ëУв û ëΖв û )ëΖв û. |
|
|
|||||||
|
|
|
|
|
|
+( |
|
|
|
|
|
|
|
é & ù |
= |
é % ù |
é & |
ù |
é % ù |
|
é % ù |
é & ù |
é % ù |
= |
|
||
ëУв û |
ëУв û + ëУ |
û= |
ë |
Ув û |
[1 ]- ëУв û |
ëΖв û ) |
ëУв û |
(3.12) |
|||||
|
|
= 2 |
é % |
ù é % |
ù é & |
ù é % |
ù |
|
|
|
|||
|
|
|
|
|
|
||||||||
|
|
ëУв û- ëУв û ëΖв û |
ëУв û. |
|
|
|
|
||||||
Таким образом, если известна приближенная обратная матрица |
é % ¢ ù |
||||||||||||
ëУв û и |
|||||||||||||
|
& |
ù , то более точная обратная матрица |
|
|
|
||||||||
исходная матрица éZ |
|
|
|
||||||||||
ë |
|
в û |
|
|
|
|
|
|
|
|
|
|
|
|
|
é % ¢ ù |
= 2 |
é % ¢ ù é % ¢ ù é |
& |
ù é % ¢ ù |
|
|
|
(3.13) |
|||
|
|
ëУв û |
ëУв |
û- ëУв û ë |
Ζв |
û ëУв û. |
|
|
|||||
Дальнейшей уточнений обратной матрицы получается путем многократного применения этой формулы до получения результата с достаточной точностью. Итерационный метод, в отличие от классического, позволяет снизить ошибку вычислений до любой приемлемой величины, если итерационный процесс является сходящимся. Сходимость же итерационного процесса зависит от правильности приближенной обратной матрицы. Если диагональные элементы исходной матрицы соизмеримы с остальными, то такой путь расчета может не привести к сходимости процесса итерации.
3.3. Прямой метод расчета матрицы узловых сопротивлений.
Описанные выше методы вычисления обратной матрицы, как отмечалось, не лишены ряда недостатков. Эти недостатки существенно усложняют процесс вычисления обратной матрицы и в ряде случаев делают его невозможным вообще. В связи с этим в настоящее время продолжают разрабатывать другие методы получения обратных матриц обобщенных параметров схем. К числу удачных разработок в этом направлении следует отнести прямой метод расчета матрицы узловых собственных и взаимных сопротивлений, предназначенный для обработки на ЭВМ сложных схем замещения систем электроснабжения.
Искомая матрица узловых сопротивлений схемы éëΖ& у ùû в этом методе
вычисляется в три этапа: на первом этапе производятся разделение схемы замещения на дерево и хорды, на втором - для полученного дерева схемы фор-
|
|
é & |
ù |
, на третьем этапе осуществ- |
мируется матрица узловых сопротивлений ëΖ0 |
û |
|||
é & |
ù |
в искомую матрицу узловых сопротивлений |
||
ляется пересчет матрицы ëΖ0 |
û |
|||
50
éëΖ& у ùû путем последовательного подключения ветвей, дополняющих дерево
до полной схемы. |
|
|
é |
& |
ù |
Математические выражения для подсчета элементов матрицыΖ |
0 û |
|
ë |
|
|
могут быть получены с использованием топологических понятий на основе применения теории линейных графов к разомкнутым электрическим схемам.
Так, согласно этой теории, узловое собственное сопротивление Ζ& 0ii матрицы
é & |
ù |
численно равно сумме сопротивлений ветвей в пути Si |
дерева от узла i |
||||
ëΖ0 |
û |
||||||
|
|
& 0 |
матрицы |
é & |
ù |
чис- |
|
до базисного узла. Узловое взаимное сопротивление Ζij |
ëΖ0 |
û |
|||||
ленно равно сумме сопротивлений ветвей общей части двух путей, а именно: пути Si в дереве от узла i до базисного узла и пути Sj от узла j до базисного
узла. Топологические формулы для расчета элементов матрицы имеют вид:
0 |
& |
& 0 |
å |
|
& |
|
|
|
|
|
|
(3.14) |
||
Zii = å Zk |
; Zij = |
|
Zk . |
|
|
|
|
|
|
|||||
|
kÎSi |
kÎ(Si n Sj ) |
|
|
|
|
|
|
|
|
|
|
||
Полученная таким образом матрица |
é & |
ù |
соответствует разомкнутой |
|||||||||||
ëΖ0 |
û |
|||||||||||||
части схемы - дереву, в то время как требуется вычислить матрицу é |
& |
ù |
для |
|||||||||||
Ζ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
ë |
|
у û |
|
|
полной сложнозамкнутой схемы. |
Пересчет матрицы |
é |
& |
|
ù |
в матрицу é |
& |
ù |
||||||
Ζ |
0 |
Ζ |
||||||||||||
|
|
|
|
|
|
ë |
|
û |
|
|
ë |
|
у û |
|
может быть выполнен по шагам. При этом на каждом шаге вычислений к схеме добавляется только одна новая ветвь.
Пересчет элементов матрицы при добавлении к схеме очередной ветви Ζ& kl производится по формуле
|
μ |
|
μ-1 |
|
(Ζik |
- Ζil |
)(Ζkj |
- Ζlj |
) |
|
|
||||
|
|
|
|
|
& μ-1 |
& μ-1 |
& μ-1 |
& μ-1 |
|
|
|
||||
& |
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ζij |
= Ζij |
- |
& μ-1 |
& |
μ-1 |
& |
μ-1 |
& μ-1 |
& |
|
, |
(3.15) |
|||
|
|
|
|
|
Ζkk |
- Ζlk |
- Ζkl |
+ Ζll |
+ Ζkl |
|
|||||
где Ζ& μij - искомый ij элемент матрицы;
Ζ& μij-1 - существующий элемент матрицы;
k, l - номера узлов, к которым присоединяется очередная ветвь.
Если новая ветвь Ζ& ko , добавленная к схеме, непосредственно соединена с базисным узлом схемы, то формула для пересчета элементов матрицы узловых сопротивлении схемы получает упрощение:
|
|
|
|
|
|
|
|
& μ-1 |
& μ-1 |
|
|
|
|
|
|
|
& μ |
& μ-1 |
|
Ζik |
Ζkj |
|
|
|
|
|
|
|
Ζij |
= Ζij |
- |
& μ-1 |
& |
. |
(3.16) |
|
|
|
|
|
|
|
|
Ζkk |
+ Ζko |
|
|
После исполнения k таких |
шагов |
вычислений |
матрица |
узловых соп- |
|||||||
ротивлений |
é & |
ù |
для дерева схемы преобразуется в матрицу узловых сопро- |
||||||||
ëΖ0 û |
|||||||||||
тивлений é |
& |
|
ù |
для полной сложнозамкнутой схемы. |
|
|
|||||
Ζ |
|
|
|||||||||
ë |
|
|
у û |
|
|
|
|
|
|
|
|
51
Описанный метод расчета матрицы узловых сопротивлений не предъявляет каких-либо требований к порядку нумерации узлов исходной схемы замещения и может быть применен при произвольной нумерации узлов. Метод позволяет довольно просто учитывать возможные изменения в схеме замещения системы электроснабжения, поскольку всякое изменение в схеме (изменение параметров схемы, подключение и отключение новых ветвей) всегда можно свести к случаю добавления одной или нескольких ветвей в исходной схеме замещения и последующему перерасчету матрицы. Метод удобен для реализации на ЭВМ.
3.4. Обращение квазидиагональных матриц.
Квазидиагональной называется квадратная клеточная матрица особой формы. Примером ее может служить следующая матрица:
é |
а |
а |
12 |
а |
0 |
0 |
ù |
|
|
|
|
ê |
11 |
|
13 |
|
|
ú |
|
|
|
|
|
êа21 |
а22 |
а23 |
0 |
0 |
ú |
é |
А |
0 ù |
|
||
[а ]= êа31 |
а32 |
а33 |
0 |
0 |
ú |
= ê |
11 |
ú . |
(3.17) |
||
ê |
|
|
|
|
|
|
ú |
ë |
0 |
А22 û |
|
0 |
0 |
0 |
а44 |
а45 |
|
||||||
ê |
ú |
|
|
|
|
||||||
ê |
0 |
0 |
0 |
а54 |
а55 |
ú |
|
|
|
|
|
ë |
û |
|
|
|
|
||||||
Приведенный пример показывает, что отличительная особенность квазидиагональной матрицы заключается в том, что все подматрицы – клетки такой матрицы – равны нулю, за исключением подматриц, расположенных на главной диагонали и имеющих квадратную форму.
Найдем матрицу, обратную матрице [а], характеризуемой выражением
(3.17), воспользовавшись общей формулой (3.5). Поскольку в рассматриваемой матрице
Α12 = 0 и Α21 = 0 ,
в этом частном случае из (3.5) следует:
B |
= A-1 |
; B = 0 ; B |
21 |
= 0 ; B |
22 |
= A-1 . |
(3.18) |
11 |
11 |
12 |
|
22 |
|
Поэтому в соответствии с (3.2) имеем
[а ]-1 |
éA |
0 ù |
-1 éA-1 |
0 |
ù |
||||
= ê |
11 |
A |
|
ú |
= ê |
11 |
|
ú , |
|
|
ë |
0 |
22 |
û |
ê |
0 |
-1 |
ú |
|
|
|
|
ë |
A22 |
û |
||||
т.е. в рассматриваемом случае обратная матрица имеет также вид квазидиагональной матрицы, причем ее элементами являются обратные матрицыклетки, составляющие квазидиагональную матрицу [а]. Этот вывод может
быть распространен на квазидиагональные матрицы с любым числом клеток. Так, например, пусть необходимо обратить квазидиагональную матрицу с тремя клетками на главной диагонали
52
éА |
0 |
|
0 |
ù |
|
||
|
|
||||||
ê |
11 |
А22 |
|
0 |
ú |
(3.19) |
|
[а ]= ê |
0 |
|
ú . |
||||
ê |
|
|
|
|
|
ú |
|
0 |
0 |
|
А |
33 |
|
||
ë |
|
|
|
|
û |
|
|
|
|
|
|
|
|||
Разбив эту матрицу на клетки, как показано в выражении (3.19), получим клеточную матрицу с двумя клетками на главной диагонали
é |
éА |
0 ù |
0 |
ù |
|
||
ê |
ê |
11 |
ú |
ú |
, |
||
[а ]= êë |
0 А22 û |
[А |
|
ú |
|||
ê |
|
|
0 |
33 |
]ú |
|
|
ë |
|
|
|
|
û |
|
|
применяя к этой матрице установленное выше правило для обращения квазидиагональных матриц с двумя клетками на главной диагонали, можем записать:
|
|
éА |
0 |
|
0 |
ù-1 |
é |
éА |
ù-1 |
|
|
|
ù |
||
-1 |
= |
ê |
11 |
|
|
0 |
ú |
ê |
ê |
11 |
ú |
|
|
|
ú |
[а ] |
ê |
0 А22 |
ú |
= ê |
ë |
|
А22 û |
|
|
|
ú = |
||||
|
|
ê |
0 |
0 |
|
А33 |
ú |
ê |
|
|
|
А |
|
-1 |
ú |
|
|
ë |
|
û |
ê |
|
|
[ |
33 |
] |
ú |
||||
|
|
|
|
|
|
|
|
ë |
|
|
|
û |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.20) |
|
|
|
|
é |
А-1 |
|
|
|
ù |
|
|
|
|
|
|
|
|
|
|
ê |
|
11 |
|
|
|
ú |
|
|
|
|
|
|
|
|
|
= ê |
|
А22-1 |
|
|
ú . |
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
А-1 |
ú |
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
ú |
|
|
|
|
|
||
|
|
|
|
ë |
|
|
|
33 |
û |
|
|
|
|
|
|
Очевидно, что таким же приемом можно получить аналогичный вывод при любом числе клеток на главной диагонали квазидиагональной матрицы.
В качестве частной формы квазидиагональной матрицы может рассматриваться матрица, у которой клетки на главной диагонали состоят лишь из одного элемента, т.е. диагональная матрица. Применяя полученное правило к этому случаю, получаем известное правило обращения диагональных матриц, в соответствии с которым для диагональной матрицы
|
|
éа11 |
а22 |
|
ù |
|
|
ê |
|
ú |
|
éа |
ù |
ê |
а33 |
. |
ú |
= ê |
|
ú |
|||
ë |
д û |
ê |
|
. |
ú |
|
|
ê |
|
. |
ú |
|
|
ê |
|
|
ú |
|
|
ë |
|
|
аnn û |
обратная матрица имеет вид:
53
