
- •Управление непрерывными динамическими тп Поиск экстремума функционалов
- •Свойства функций и функционалов
- •Классическое вариационное исчисление Метод Эйлера для определения экстремальных функций без ограничений
- •Решение вариационной задачи на безусловный экстремум при различных заданиях подынтегральной функции в функционале
- •Решение вариационных задач на условный экстремум (метод Эйлера-Лагранжа)
- •Решение задач акр с помощью кви
- •Решение задач акр с помощью метода Эйлера-Лагранжа
- •Решение неклассических задач вариационного исчисления
- •Принцип максимума
- •I. Решение задачи без ограничений на u.
- •II. Решение задачи с ограничениями.
- •Оптимальное по быстродействию управление линейными объектами
- •Теорема об nинтервалах
- •Нелинейные задачи оптимального управления
Решение задач акр с помощью метода Эйлера-Лагранжа
Для функционала
![]() при уравнениях связи
при уравнениях связи![]() ,
,![]() составляется функционал
составляется функционал
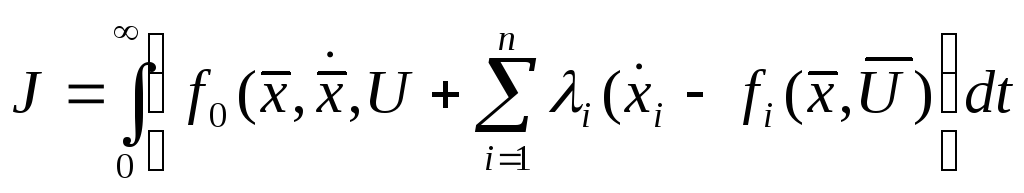 ,
,
к которому
применяются уравнения Эйлера по
переменным
![]() и
и![]() .
.
Р ассмотрим
пример решения задачи АКР для колебательного
звена:
ассмотрим
пример решения задачи АКР для колебательного
звена:
![]()
Как известно из
ТАУ при
![]() – апериодический процесс,
– апериодический процесс,![]() – незатухающие колебания.
– незатухающие колебания.
Имеем колебательное звено
![]() .
.
З апишем
дифференциальное уравнение второго
порядка в виде системы двух уравнений
первого порядка, для чего введем
переменные
апишем
дифференциальное уравнение второго
порядка в виде системы двух уравнений
первого порядка, для чего введем
переменные![]() ,
,![]() ,
тогда
,
тогда![]() .
Итак имеем систему:
.
Итак имеем систему:
 , (4)
которой соответствует структура:
, (4)
которой соответствует структура:
и функционал
![]() .
.
Граничные условия:
![]() ,
,
![]()
![]() ,
,
![]() .
Требуется найти
.
Требуется найти![]()
Решение:
Составляется уравнение Лагранжа
![]()

Подставив
![]() во второе уравнение системы (4) получаем
следующую систему уравнений с неизвестными
во второе уравнение системы (4) получаем
следующую систему уравнений с неизвестными![]() ,
,![]() ,
,![]() ,
,![]() :
:
 , (5)
, (5)
Характеристический определитель системы (5):
 , (6)
, (6)
Обозначим
![]() ,
,![]() .
С учетом введенных обозначений,
характеристическое уравнение запишется:
.
С учетом введенных обозначений,
характеристическое уравнение запишется:
![]() .
.
Решаем его обозначая
![]() :
:
![]()
![]()
Случай 1.
Пусть
![]() .
Если
.
Если![]() ,
то все корни исходного характеристического
уравнения чисто мнимые и оптимальный
регулятор не существует. Если
,
то все корни исходного характеристического
уравнения чисто мнимые и оптимальный
регулятор не существует. Если![]() ,
то корни будут иметь вид:
,
то корни будут иметь вид:
![]()
![]()
В общем виде решением системы (5) будет
![]() ,
,
причем
![]() в силу граничных условий. Из уравнения
в силу граничных условий. Из уравнения![]() получим решение для
получим решение для![]() :
:
![]() .
.
Далее, исключаем время из решения для синтеза регулятора. Получим:
![]()
![]() ,
,
подставляя которые
в уравнение для
![]() находим:
находим:
 .
.
Из второго уравнения системы (4) находится уравнение оптимального регулятора
![]() .
.
Случай 2.
Пусть
![]() .
Тогда корни характеристического
уравнения (6) будут комплексными:
.
Тогда корни характеристического
уравнения (6) будут комплексными:
![]() ,
,
![]() ,
,
где
![]() ,
,![]() .
.
В общем случае решение системы (5) для этого случая:
![]() ,
,
причем, в силу
граничных условий
![]() .
.
Выразив производную
![]() через переменные
через переменные![]() и
и![]() :
:
![]() ,
,
из второго уравнения системы (4) получим уравнение оптимального регулятора:
![]()
Таким образом, для
оптимизации по квадратичному критерию
колебательного звена необходимо
замкнуть его отрицательной обратной
связью по выходным координатам с
коэффициентами соответственно
![]() и
и![]() .
.
Структурная схема замкнутой системы:

Отметим, что от выбора весовых коэффициентов в функционале зависит характер переходного процесса в системе. Процесс может быть колебательным или монотонным, иметь различное перерегулирование и т.д. Если найти в общем виде уравнение для функционала в зависимости от весовых коэффициентов, то можно провести минимизацию функционала по параметрам, в качестве которых выступают коэффициенты штрафа.
Решение неклассических задач вариационного исчисления
Неклассическими задачами ВИ считаются такие, в которых накладываются ограничения в виде неравенств на переменные системы и управления, что всегда встречается в технических задачах. Рассмотрим основной метод их решения, получивший название принцип максимума. Этот аппарат разработан в середине 50-х годов XXвека коллективом отечественных ученых под руководством Понтрягина Л.С. За разработку коллектив получил Ленинскую премию. С тех пор метод продолжает развиваться.
Принцип максимума
Постановка задачи.
Пусть объект управления описывается системой уравнений
![]() ,
,
![]() , (1)
, (1)
или в векторной форме
![]() ,
,
где
![]() – вектор координат состояния,
– вектор координат состояния,![]() – вектор управлений.
– вектор управлений.
Полагаем, что
функции
![]() непрерывны по всем аргументам и имеют
непрерывные частные производные по
непрерывны по всем аргументам и имеют
непрерывные частные производные по![]() .
На переменные системы и управления
наложены ограничения
.
На переменные системы и управления
наложены ограничения![]() ,
,![]() (это первое отличие от классического
вариационного исчисления).
(это первое отличие от классического
вариационного исчисления).
Назовем допустимыми
управлениями такие управления
![]() ,
которые являются кусочно-непрерывными
функциями времени и принимают значения
из области
,
которые являются кусочно-непрерывными
функциями времени и принимают значения
из области![]() .
(Кусочная непрерывность – это второе
отличие). Кусочная непрерывность
означает, что имеем негладкую функцию,
но она непрерывна по
.
(Кусочная непрерывность – это второе
отличие). Кусочная непрерывность
означает, что имеем негладкую функцию,
но она непрерывна по![]() для
для![]() в силу того, что
в силу того, что![]() непрерывны.
непрерывны.
Для управлений же функции могут иметь разрывы.

Задача формулируется
следующим образом: среди допустимых
управлений, переводящих систему в
пространстве
![]() из начального положения
из начального положения![]() в конечное положение
в конечное положение![]() ,
если эти управления существуют, требуется
найти такое управление
,
если эти управления существуют, требуется
найти такое управление![]() ,
для которого функционал
,
для которого функционал
 (2)
(2)
достигает минимума.
Идея метода.
Введем в рассмотрение
новую координату состояния
![]() ,
удовлетворяющую дифференциальному
уравнению
,
удовлетворяющую дифференциальному
уравнению
![]() , (3)
, (3)
которое учитывает подынтегральную функцию в функционале (2). Присоединив уравнение (3) к системе (1) получим систему уравнений:
![]() ,
,
![]() , (4)
, (4)
Запишем систему
(4) в векторной форме, для чего введем в
рассмотрение (n+1)-мерный
вектор координат состояния![]() .
Тогда в векторной форме система уравнений
(4) примет вид:
.
Тогда в векторной форме система уравнений
(4) примет вид:
![]() , (5)
, (5)
где
![]() – вектор правых частей системы (4), причем
правые части не зависят от координаты
– вектор правых частей системы (4), причем
правые части не зависят от координаты![]() .
.
Обозначим в
(n+1)-мерном пространстве
состояний через![]() точку с координатами
точку с координатами![]() .
Пусть
.
Пусть![]() – некоторое допустимое управление, для
которого соответствующая фазовая
траектория системы (1) проходит при
– некоторое допустимое управление, для
которого соответствующая фазовая
траектория системы (1) проходит при![]() через точку
через точку![]() ,
а при
,
а при![]() – через точку
– через точку![]() .
Из уравнения (3) следует, что координата
.
Из уравнения (3) следует, что координата
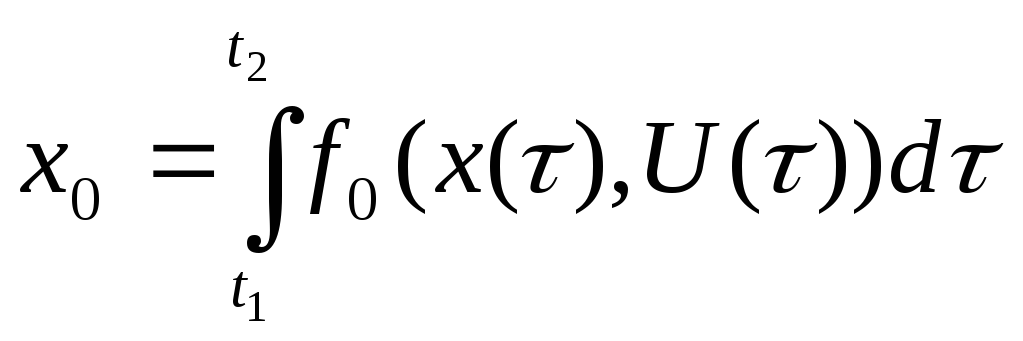 .
.
При
![]() эта координата
эта координата

Таким образом, в
пространстве
![]() фазовая траектория
фазовая траектория![]() системы (5) при этом управлении проходит
при
системы (5) при этом управлении проходит
при![]() через точку
через точку![]() ,
а при
,
а при![]() через точку
через точку![]() .
Тогда задачу оптимального управления
можно сформулировать так:
.
Тогда задачу оптимального управления
можно сформулировать так:
Для системы
![]() следует выбрать такое управление, чтобы
координата
следует выбрать такое управление, чтобы
координата![]() принимала бы наименьшее значение, т.к.
подразумевается, что отыскивается
минимум функционала.
принимала бы наименьшее значение, т.к.
подразумевается, что отыскивается
минимум функционала.
Доказательство метода сводится к доказательству некоторых утверждений:
Утверждается принцип оптимальности, что каждый отрезок оптимальной траектории является оптимальным. На основе его показывается, что все неоптимальные траектории проходят выше оптимальной. Если какая-то траектория проходит ниже выбранной, то ее нужно считать за оптимальную. Далее задаются вариации траекторий при воздействии различных вариаций управления. Считается, что найдено оптимальное управление, соответствующее оптимальной траектории.
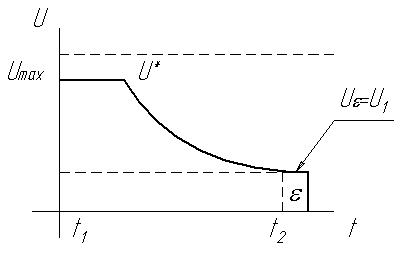
Задается временная вариация управления в течение времени
 ,
в конце управления
,
в конце управления .
.


![]()
Доказывается, что
остаток Rвариации
траектории является малым, а движение
при временной вариации будет проходить
по касательной в конечной точке (вектор![]() ).
).
Задается игольчатая вариация управления (вариация Макшейна).
Э та
вариация ограничена. Если
та
вариация ограничена. Если![]() ,
то площадь импульса также
,
то площадь импульса также![]() ,
при этом следует ожидать малого отклонения
варьированной траектории от оптимальной.
,
при этом следует ожидать малого отклонения
варьированной траектории от оптимальной.
В принципе максимума
доказывается, что варьированные
траектории будут выше оптимальной и
они получаются путем сдвига оптимальной
траектории на величину
![]() .
.
![]()
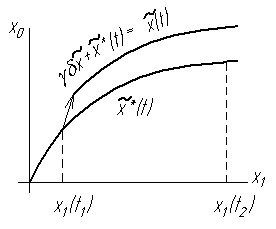 .
.
Дается множество
игольчатых вариаций, от каждой вариации
получается вектор смещения
![]() .
Все векторы смещения переносятся в
конечную точку. На векторы смещения
натягивается оболочка – получается
конус векторов смещения
.
Все векторы смещения переносятся в
конечную точку. На векторы смещения
натягивается оболочка – получается
конус векторов смещения![]() .
.
4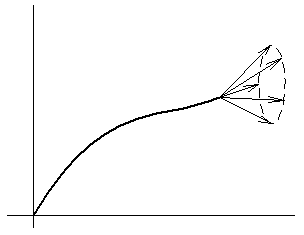 .
Полученный конус векторов смещения от
игольчатых вариаций
.
Полученный конус векторов смещения от
игольчатых вариаций![]() растягивается по направлению вектора
растягивается по направлению вектора![]() от временной вариации. Полученный конус
от временной вариации. Полученный конус![]() не заполняет всего (n+1)-мерного
пространства. Т.к. конус построен на
вариациях, то оптимальная траектория
не попадает в этот конус. Раз так, то
этот конус можно отделить от траектории
некоторой плоскостью. Эту плоскость
характеризует вектор
не заполняет всего (n+1)-мерного
пространства. Т.к. конус построен на
вариациях, то оптимальная траектория
не попадает в этот конус. Раз так, то
этот конус можно отделить от траектории
некоторой плоскостью. Эту плоскость
характеризует вектор![]() ,
нормальный к плоскости. Вектор же
,
нормальный к плоскости. Вектор же![]() лежит в этой плоскости, т.е они
перпендикулярны и их скалярное
произведение равно нулю. С учетом
лежит в этой плоскости, т.е они
перпендикулярны и их скалярное
произведение равно нулю. С учетом![]() ,
получим:
,
получим:
![]() .
.
В ПМ также
доказывается, что векторы
![]() и
и![]() перемещаются вдоль траектории и всегда
перпендикулярны, т.е. их скалярное
произведение должно быть равно 0.
перемещаются вдоль траектории и всегда
перпендикулярны, т.е. их скалярное
произведение должно быть равно 0.
Определение
вспомогательной вектор-функции ![]() .
.
Стоит задача –
выразить функцию
![]() через уравнения связи.
через уравнения связи.
Запишем неоптимальную траекторию через оптимальную и вариацию.
![]()
и подставим в уравнение связи.
![]() , (*)
, (*)
![]() записывается без
вариации
записывается без
вариации
![]() ,
т.к. в ПМ доказывается, что
,
т.к. в ПМ доказывается, что![]() при
при![]() на порядок ниже, чем вызванная им вариация
на порядок ниже, чем вызванная им вариация![]() .
.
Разложим правую часть уравнения (*) в ряд Тейлора и воспользуемся только линейной частью разложения:
![]() , (**)
, (**)
где
![]() в (n+1)-мерном пространстве,
в (n+1)-мерном пространстве,![]() вn-мерном пространстве.
вn-мерном пространстве.
Потребуем, чтобы скалярное произведение векторов
![]() , (***)
, (***)
вдоль описанной
траектории. Из ПМ было видно, что
![]() ,
поэтому условие (***) более слабое, чем
равенство 0 этого произведения.
,
поэтому условие (***) более слабое, чем
равенство 0 этого произведения.
Далее попытаемся найти вектор-функцию
![]()
С начала
определим вектор
начала
определим вектор![]() для чего рассмотрим следующее. Приращение
функционала относительно оптимальной
траектории
для чего рассмотрим следующее. Приращение
функционала относительно оптимальной
траектории
![]() ,
,
что ясно из
доказательства ПМ. Видно, что
![]() .
Приращение
.
Приращение![]() идет по линии П, нам важно знать только
направление
идет по линии П, нам важно знать только
направление![]() .
Для проварьированной траектории примем
.
Для проварьированной траектории примем![]() равной 1 > 0. Т.е.
возьмем
равной 1 > 0. Т.е.
возьмем![]() .
Потребуем, чтобы скалярное произведение
.
Потребуем, чтобы скалярное произведение
![]() ,
,
что возможно при
![]() .
.
Для нахождения вспомогательных функций
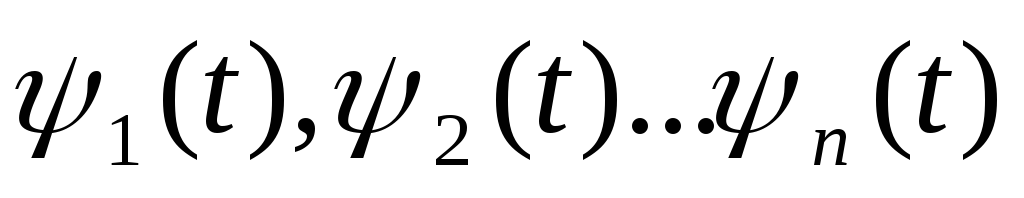 продифференцируем по времени уравнение
(***):
продифференцируем по времени уравнение
(***):
![]() .
.
Запишем последнее уравнение не в векторной, а в координатной форме:
![]() .
.
Т.к.
![]() ,
то
,
то![]() ,
т.е. вторую сумму можно записать как
,
т.е. вторую сумму можно записать как
![]() .
.
Воспользовавшись (**), получим:
![]()
 .
.
Из этого можно
записать уравнения для
![]() :
:
![]() . (6)
. (6)
Следует отметить,
что уравнения связи в (n+1)-мерном
пространстве (5) и уравнения для
вспомогательных переменных (6) можно
объединить одной формой записи. Для
этого вводится т.н. функция Гамильтона![]() переменных
переменных![]() ,
,![]() ,
,![]() :
:
![]() .
.
Тогда предыдущие системы уравнений можно записать
![]() ,
,
![]()
![]() ,
,
![]()
![]() и
и
![]() – непрерывны и всюду, кроме точек
разрыва, имеют непрерывную производную.
– непрерывны и всюду, кроме точек
разрыва, имеют непрерывную производную.
При фиксированных
значениях
![]() и
и![]() функция
функция![]() становится только функцией управления
становится только функцией управления![]() .
Обозначим через
.
Обозначим через
![]() .
.
Основная теорема ПМ звучит так:
Пусть
![]() ,
где
,
где![]() – такое допустимое воздействие, что
соответствующая ему фазовая траектория
– такое допустимое воздействие, что
соответствующая ему фазовая траектория![]() исходящая в момент
исходящая в момент![]() из
из![]() ,
проходящая в момент
,
проходящая в момент![]() через некоторую точку прямой П.
через некоторую точку прямой П.
Для оптимальности
управления
![]() и траектории
и траектории![]() необходимо существование такой ненулевой
непрерывной вектор-функции
необходимо существование такой ненулевой
непрерывной вектор-функции![]() ,
соответствующей функциям
,
соответствующей функциям![]() и
и![]() и удовлетворяющей уравнению
и удовлетворяющей уравнению
![]() или (6),
или (6),
что:
при любом
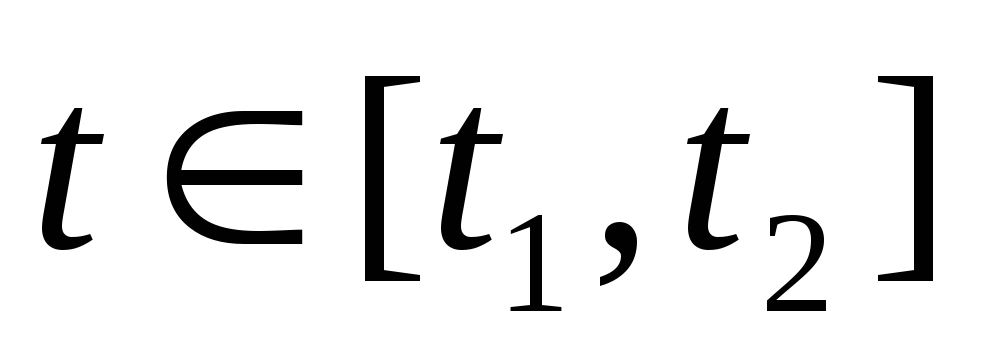 функция
функция достигает по
достигает по максимума, т.е.
максимума, т.е.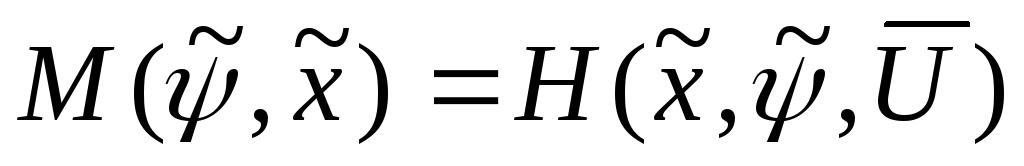 .
.в конечный момент времени
 имеет место соотношение
имеет место соотношение
![]() ,
а
,
а
![]() .
.
Если процесс оптимален, то эти условия выполняются на всей траектории.
Рассмотрим пример на применение ПМ.
Для объекта
![]() с граничными условиями
с граничными условиями![]() ,
,![]() требуется найти
требуется найти![]() ,
минимизирующее функционал
,
минимизирующее функционал
![]() .
.
