14. Логарифмический критерий устойчивости Найквиста. (3 стр. 31-33)

Критерий Найквиста можно использовать и по отношению к ЛЧХ. Согласно критерию устойчивости Найквиста САР устойчива, если при (1)

Если использовать логарифмический масштаб, то это означает, что

(2)

Условие (2) можно сформулировать следующим образом:

Если ФЧХ системы в разомкнутом состоянии при частоте среза (то есть при частоте, где ЛАЧХ пересекает ось абсцисс) не достигает значения , то система в замкнутом состоянии устойчива.

Об устойчивости замкнутой САР можно судить по расположению ЛЧХ встречно-параллельных соединяемых звеньев, не прибегая к непосредственному построению ЛЧХ САР в разомкнутом состоянии.

Доказано, что любая замкнутая САР представляется в виде встречно-параллельного соединения звеньев.

Для построения ЛЧХ замкнутой САР необходимо построить характеристики ,,,и определить поправки.

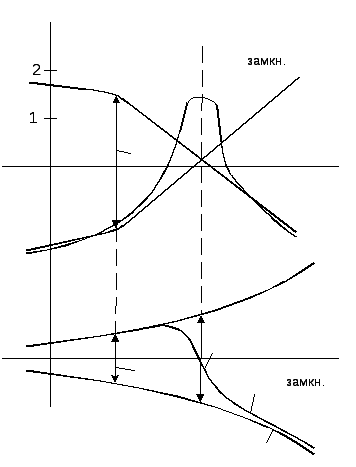
Как известно,

Из рисунка видно, что

то есть ординаты между ЛАЧХ и ЛФЧХ прямого и обратного канала представляют собой значения соответственно ЛАЧХ и ЛФЧХ системы в разомкнутом состоянии.

Таким образом, применительно к рассмотренному соединению звеньев критерий устойчивости Найквиста может быть сформулирован следующим образом: САР устойчива в замкнутом состоянии, если в точке пересечения ЛАЧХ прямого канала и обратного ЛАЧХ канала обратной связи разность фаз между ЛФЧХ прямого канала и обратного ЛФЧХ канала обратной связи меньше .

15. Типовые желаемые лачх. (2 стр. 34-35)

Как уже отмечалось ранее, важным требованием к САУ в динамике является условие , чтобы САУ отрабатывала управляющее воздействие в минимально возможное время и с наименьшей колебательностью и не реагировала на возмущающее воздействия.

Пусть имеется САР, у которой существует однозначная зависимость между ЛАЧХ и ЛФХ (минимально-фазовая САР) вида:

Заданную структурную схему можно преобразовать к виду:

т.е. по заданию по возмущению

а) б) для зависимостей

в) для ЛАЧХ замкнутой САР г) для ЛАЧХ системы в разомкнутом состоянии

;;

т.н. betrags оптиум (оптиум с однократным интегрированием)

,

где Т сумма малых пост. времени

Таким образом желаемая характеристика находится:

Поскольку основную роль играет ЛАХ в районе частоты среза, то в некоторых случаях для предварительного выбораLр жел. используется следующая методика:

т.е. используется т.н. симметричный оптиум с 2-х кратным интегрированием

при этомW

где Т-сумма малых постоянной времени рассматриваемой САР.

16. Последовательная коррекция (2 стр 36-37)

В зависимости от схемы включения корректирующие устройства делятся на последовательные и параллельные. В первом случае кор­ректирующее устройство включается последовательно в цепь основ­ного воздействия, во втором - в цепь обратной связи охватывающей одно или не­сколько звеньев САР.

а) включение последовательно корректирующего звена:

W(Р) - перед.ф-ция посл.кор.устр;

W(Р) - перед.ф-ция эл-тов неизм. части САР.

б) включение параллельно корректирующего звена:

W(Р)- перед. функция элементов САР, в о.с. которых находятсяпараллельно корректирующие устройства.

W(Р) - перед. функция остальных элементов неизменяемой

части САР.

W(Р) - передаточная функция корректирующего параллельного

устройства.