Работа №1 (1)

ГОУ ВПО

"Российский Экономический университет имени Г.В.Плеханова"

Кафедра

"Математические методы в экономике"

Контрольная работа №1

по дисциплине

"Эконометрика"

Выполнил:

студент финансового факультета

гр. 2304

Проверил:

Колпаков В. Ф.

Москва – 2011

Задание 6.4

По территориям региона известны данные за 2006 г.

1. Постройте корреляционное поле и по его виду определите форму зависимости между X и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров X и Y.

4. проверьте качество уравнения регрессии:

а) значимость коэффициентов регрессии;

б) интервальные оценки коэффициентов регрессии;

в) значимость уравнения регрессии в целом

5. Проинтерпретируйте результаты.

6. Сделайте прогноз потребительских расходов при средней заработной плате и выплатах социального характера X=X_прогн.

Номер района	Потребительские расходы на душу населения Y, тыс. руб	Средняя заработная плата и выплаты социального характера Х, тыс. руб.
1	3,8	5,9
2	5,0	8,6
3	6,7	11,3
4	8,5	15,0
5	7,0	12,1
6	6,0	9,4
7	5,4	7,9
8	6,3	10,5

X_прогн.=16; уровень значимости = 0,04

1. Построим корреляционное поле с помощью Мастера диаграмм, используя данные по средней заработной плате и доле денежных доходов в Северном и Северо-Западном регионах.

По данному расположению точек на графике можно сделать выводы о линейной зависимости между средней заработной платы и выплаты социального характера и потребительскими расходами на душу населения.

2. Оцените по МНК параметры уравнения линейной регрессии.

; .

Рассчитаем коэффициенты уравнения линейной регрессии двумя способами.

= 0,49753

= 1,06870

= 1,06870 + 0,49753*

Коэффициент показывает тесноту связи между x и y. При увеличении зарплаты на единицу, прирост сбережений будет составлять 0,49753.

3. Выборочный коэффициент корреляции

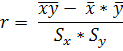
= 2,617937

= 1,321398

r = 0,985693

Полученное значение говорит о довольно сильной связи между средней заработной платы и выплаты социального характера и потребительскими расходами на душу населения. Число положительное, а значит связь тоже положительная (между средней заработной платы и выплаты социального характера и потребительскими расходами на душу населения увеличиваются прямопропорционально).

4. Проверка качества уравнения регрессии.

По таблице критических точек Стьюдента, находим = 2,612241845 (уровень значимости α = 0,04, в таблицу входим со значениями: α/2 = 0,02, и ν = n – 2 = 8 – 2 = 6 степенями свободы).

а) Оценка значимости коэффициентов регрессии.

Найдем S, , .

= = 0,066142003; Отсюда S =0,257180876.

= -( )² = 6,8536

= /n* = 0,001206; Отсюда = 0,034732.

= * = 0,131022; Отсюда = 0,361969.

Проверим значимость обоих коэффициентов:

Значимость

: = 0

: ≠ 0

T_b1 = / = 0,49753/0,034732= 14,32457

Данное значение не входит в интервал ±, следовательно, принимаем гипотезу : ≠ 0, это говорит нам о том, что коэффициент значим.

Значимость

: = 0

: ≠ 0

T_b0 = / = 1,06870/0,361969=2,952466

Данное значение тоже не входит в интервал ±, следовательно, принимаем гипотезу и является значимым. Этот коэффициент показывает долю пенсии.

б) Интервальные оценки коэффициентов регрессии.

Найдем доверительные интервалы.

- * ₁ + *

0,406797022 1 0,588255756

₁ϵ (0,406797022; 0,588255756)

- * ₀ + *

0,123150837 0 2,014254265

₀ϵ(0,123150837; 2,014254265)

Эти доверительные интервалы показывают диапазон вокруг значения наших случайных величин и , и мы можем с уверенностью 95% заявлять, что истинные значения попадут в пределы этого интервала.

в) Значимость уравнения регрессии в целом.

Мерой общего качества уравнения регрессии является коэффициент детерминации R² :

R² = 1 – е_i² / ( y_i - )²

( y_i - )²= k_I² + e²_i=7,666758 + 0,39685=8,063608

R² = 1 – (0,39685/8,063608)= 0,950785

Полученное значение показывает, что данная математическая модель, которая описывается уравнением регрессии = 2,557317 + 0,713415, на 5% достоверно описывает экспериментальные данные, и было использовано достаточное количество переменных.

6. Прогноз денежных доходов, направленных на прирост сбережений и доверительный интервал для нее, при значении X = = 16.

Вычислим прогнозируемое значение пенсии, при оплате труда 3 тыс. руб.

= 1,06870 + 0,49753*=9,02918

= 2,612241845 (уровень значимости α = 0,04, в таблицу входим со значениями: α/2 = 0,02, и ν = n – 2 = 8 – 2 = 6 степенями свободы).

а) Интервальный прогноз для среднего значения вычисляется следующим образом:

_р t_кр S ,

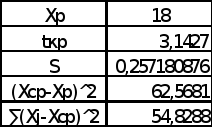
построим дополнительную таблицу:

от	Yp	до
8,273010774	9,02918	9,938901675

Доверительный интервал будет заключен в [8,119458325; 9,938901675]. Следовательно, при прогнозируемом значении прожиточного минимума в 3 тыс. руб., мы можем спрогнозировать пенсию в размере 9,02918 тыс. руб.

б)Интервальный прогноз для индивидуального значения вычисляется следующим образом:

_р t_кр * S*

от	Yp	до
8,017680029	9,02918	10,040519