
02
.doc2.
Вращательное движение.
Вращательное движение твердого тела-движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения.
Угловая скорость. Векторная величина, определяемая первой производной угла поворота тела по времени:
![]() .
.
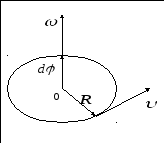
Вектор![]() направлен вдоль оси вращения по правилу
правого винта, т.е. так же, как и вектор
направлен вдоль оси вращения по правилу
правого винта, т.е. так же, как и вектор
![]() .
.
(единица угловой скорости [1 рад/с])
Период вращения (Т) ( при
![]() )
)
Время, за которое точка совершает один
полный оборот, т.е. поворачивается на
угол 2. Так как
промежутку времени t
= T соответствует
![]() = 2, то
= 2, то
![]() = 2/T,
откуда:
= 2/T,
откуда:
![]() .
.
Элементарные углы поворота
![]() .
.
Рассматривают как векторы. Модуль
вектора
![]() равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
Линейная скорость точки.
![]() .
.
Частота вращения (n).
Число полных оборотов, совершаемых
телом при равномерном его движении
по окружности, в единицу времени
![]() ,
откуда
,
откуда
![]() .
.
(единица частоты вращения 1/с).
Угловое ускорение. Связь между линейной скоростью и тангенсальным ускорением.
Угловое ускорение
![]() -векторная
величина, определяемая первой произвольной
угловой скорости по времени:
-векторная
величина, определяемая первой произвольной
угловой скорости по времени:
![]() .
.
Направление вектора (![]() ).
).
При вращении тела вокруг непосредственной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.
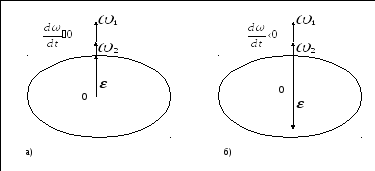
При ускоренном движении вектор
![]() сонаправлен вектору
сонаправлен вектору
![]() (а), при замедленном-противонаправлен
ему (б).
(а), при замедленном-противонаправлен
ему (б).
Связь между линейными и угловыми величинами.
Тангенсальная составляющая ускорения
![]() .
.
Нормальная составляющая уравнения
 .
.
Связь между линейными (длина пути s,
пройденного точкой по окружности радиуса
R, линейная скорость
![]() ,
тангенсальное ускорение
,
тангенсальное ускорение
![]() ,
нормальное ускорение
,
нормальное ускорение
![]() )
и угловыми величинами (угол поворота
)
и угловыми величинами (угол поворота
![]() ,
угловая скорость
,
угловая скорость
![]() ,
угловое ускорение
,
угловое ускорение
![]() )
выражается след. формулами:
)
выражается след. формулами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Псевдовекторы.
Векторы
![]() ,
направления которых связываются с
направлением вращения, называются
псевдовекторами, или аксиальными
векторами. Эти векторы не имеют
определенных точек приложения: они
могут откладываться из любой точки оси
вращения.
,
направления которых связываются с
направлением вращения, называются
псевдовекторами, или аксиальными
векторами. Эти векторы не имеют
определенных точек приложения: они
могут откладываться из любой точки оси
вращения.
