sbornik2011.pdf (страница 353) Скоромолов И.О

3. Официальный сайт «Почта России». [Электронный ресурс]. Режим доступа: http://www.почта-россии.рф/.

А.П. Филимонов, Е.Ю. Клепикова, С.В. Мкртычев

РАЗРАБОТКА ПОДСИСТЕМЫ АНАЛИЗА ДАННЫХ СТРАХОВОЙ

КОМПАНИИ ОАСО «АСТРО-ВОЛГА»

Научный руководитель: С.В. Мкртычев, к.т.н., доцент

Филиал РГГУ в г.Тольятти kaf_miend@tfrggu.ru

Как показал современный этап развития страхового бизнеса, в условиях кризиса возрастает роль менеджмента страховой компании, эффективность решений которого во многом будет зависеть от возможностей используемой в компании информационной аналитической системы.

Информационная аналитическая система – это комплекс аппаратных, программных средств, информационных ресурсов, методик, которые используются для обеспечения автоматизации аналитических работ в целях обоснования принятия управленческих решений.

Объемы информации, необходимой и используемой при принятии решений, достигают десятков гигабайт, а в крупных страховых компаниях - и того больше. Информация характеризуется многоплановостью, сложностью отображаемых объектов и систем, а также связей между объектами, явлениями и процессами, скрытостью закономерностей.

Внедрение современных информационных систем, обладающих аналитической функциональностью не только существенно упростит принятие решений, но и гарантирует минимизацию ошибок, что особенно важно в условиях жесткой конкуренции.

Подсистема анализа данных (информационно-аналитическая подсистема - ИАП) является внешней подсистемой, интегрируемой с существующей в компании ОАСО «АСтрО-Волга» КИС СК.

Устойчивый рост объемов корпоративных данных ОАСО «АСтрОВолга» и повышение роли планово-экономического отдела (ПЭО) в принятии управленческих решений показали, что для быстрого принятия управленческого решения необходимо автоматизировать работу анализа данных с помощью современных информационных технологий и средств ВТ,

вчастности – с помощью ИАП.

Всвязи с этим был проведен анализ исследуемой модели бизнеспроцесса анализа данных страховой компании ОАСО «АСтрО-Волга» «КАК ЕСТЬ» (рис. 1) и сформулированы требования к модели «КАК ДОЛЖНО БЫТЬ»:

- обеспечение автоматизации бизнес-процесса анализа данных с помощью отдельной ИАП;

430

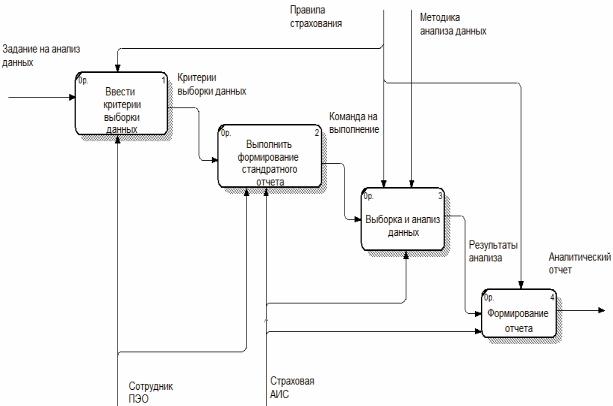
- реализация ИАП на основе OLAP – технологии.

Рис. 1 DFDдиаграмма «КАК ЕСТЬ» бизнес-процесса анализа данных в страховой компании

Модель бизнес-процесса анализа данных для страховой компании ОАСО «АСтрО-Волга» «КАК ДОЛЖНО БЫТЬ» представлена на рис. 2.

Анализ известных ИТ-решений показал, что они не удовлетворяют в полной мере требованиям, предъявляемым к новой ИАП. В этой связи принято решение о разработке ИАП с учетом новых требований.

По результатам анализа предлагается использовать при реализации ИАП двухзвенную архитектуру «клиент-сервер». Для обеспечения гибкости ИАП по согласованию с заказчиком принято решение экспортировать многомерные данные из хранилища данных в табличный процессор Microsoft Excel 2007. В качестве СУБД для реализации ROLAPсистемы выбираем

MS SQL Server 2005.

При разработке ИАП были учтены следующие требования заказчика:

система должна работать в сетевом режиме;

простота встраивания АИС в существующую в страховой компании ИТинфраструктуру;

простота в использовании и сопровождение;

минимальные затраты на приобретение и эксплуатацию.

431

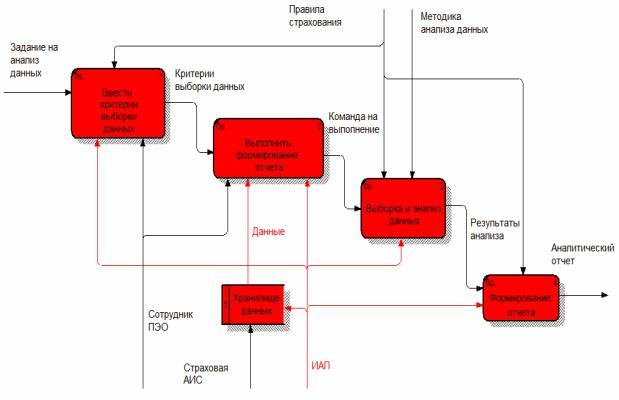
Рис. 2 DFD-диаграмма «КАК ДОЛЖНО БЫТЬ» бизнес-процесса анализа данных в страховой компании

Анализ аппаратного обеспечения КИС СК страховой компании подтвердил его соответствие требованиям, предъявляемым к аппаратному обеспечению ИАП.

Таким образом, разработанная информационно-аналитическая подсистема позволит оптимизировать решение задач, связанных с принятием оперативных управленческих решений, поможет экспертам компании ОАСО «АСтрО-Волга» быстро и качественно анализировать большие объемы данных.

Литература

1.Федеральный закон Российской Федерации «Об информации, информационных технологиях и о защите информации» от 27 июля 2006

г. N 149-ФЗ.

2.Барсегян, А.А. Технологии анализа данных. / А.А. Барсегян, М.С. Куприянов, В.В. Степаненко, И.И. Холод. - СПб.: BHV, 2008. – 384 с.

3.Мкртычев, С.В. Автоматизированные информационные системы в страховании: учеб.-метод. пособие / С.В. Мкртычев. – Тольятти: ТГУ, 2008. - 94 с.

432

С.Д. Чуев

ПРИМЕНЕНИЕ МЕТОДОВ МОДЕЛИРОВАНИЯ ПРИ

АВТОМАТИЗАЦИИ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ.

СИМПЛЕКС МЕТОД

Научный руководитель: Н.П. Лыкова

Филиал РГГУ в г.Самара srggu@mail.ru

Моделирование

Разработчики современных информационных систем постоянно сталкиваются с ростом их сложности. Это связано с повышением числа требований к системам, применением более сложных архитектурных решений (например, с переходом от простых двухзвенных клиент-серверных систем к распределенным многозвенным) и, как следствие, с увеличением объемов программного кода. В этих условиях разработка системы путем прямого перехода от требований к программированию приводит к огромному количеству ошибок, в результате чего такие проекты обычно остаются незавершенными. Сейчас уже достаточно ясно всем, что создание современных ПС невозможно без модельно-базированного подхода.

Модель ПС создается для того, чтобы лучше понимать разрабатываемую систему. Если система достаточно сложная, то другого способа понять, ее как единое целое для человека просто нет.

Проектирование ПС начинается с построения модели, описывающей систему с разных точек зрения. Это означает, что полная модель складывается из отдельных проекций, отражающих разные аспекты системы. Выбор проекций модели зависит от подхода к проблеме и принятых решений. Ключом к построению проекций является абстрагирование, когда сосредоточиваются на наиболее существенных деталях, игнорируя при этом менее важные. В дальнейшем для краткости каждую проекцию мы будем называть моделью, указывая ее тип. Например, функциональная модель показывает, что делает система в ответ на запросы пользователя (но не как она это делает), логическая модель описывает основные сущности и отношения между ними.

Модели позволяют свести высокую сложность ПС до уровня, понимаемого человеком. Достигается это за счет иерархического принципа их построения и применения наглядной графической нотации. Иерархия уровней описания системы дает возможность резко сократить количество элементов, которые должен анализировать человек. Каждая модель может быть выражена с разными уровнями детализации. При этом на верхних уровнях иерархии опускаются детали реализации, которые проявляются на более низких уровнях. Руководители проекта могут работать с верхним уровнем модели, где отражаются только основные классы, объекты и связи.

433

Другие разработчики или эксперты имеют возможность опускаться до более мелких, терминальных объектов, их свойств, связей, методов.

В процессе построения модели ПС принимаются наиболее ответственные архитектурные решения, поскольку для этого не требуется детальное кодирование. Таким образом, происходит разделение труда: моделирование ПС выполняется обычно наиболее квалифицированными разработчиками, способными принять и обосновать кардинальные решения, программную реализацию могут осуществлять программисты среднего уровня, воплощающие принятые и отраженные в модели системные решения в программных кодах.

Процесс моделирования

Процесс моделирования включает три элемента:

1.субъект (исследователь),

2.объект исследования,

3.модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.

Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой

идостаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.

На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о ее «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.

На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.

Четвертый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.

434

Моделирование — циклический процесс. Это означает, что за первым четырехэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.

Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.

Линейное программирование

В экономической теории широко используются методы научной абстракции, анализа и синтеза, системный подход, методы моделирования (прежде всего графический, математический и компьютерного моделирования).

Линейное программирование - раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Симплекс метод

Для решения задач линейного программирования существует множество методов. Рассмотрим один из них.

Улучшенный (модифицированный) симплекс-метод

Для начала расскажем, что такое симплекс-метод. Слово SIMPLEX в обычном смысле означает простой, несоставной, в противоположность слову

COMPLEX.

Данный метод получил несколько различных форм (модификаций) и был разработан в 1947 году Г. Данцигом.

Сущность симплекс-метода заключается в том, что если число неизвестных больше числа уравнений, то данная система неопределенная с бесчисленным множеством решений. Для решения системы все неизвестные произвольно подразделяют на базисные и свободные. Число базисных переменных определяется числом линейно-независимых уравнений. Остальные неизвестные свободные. Им придают произвольные значения и подставляют в систему. Любому набору свободных неизвестных можно придать бесчисленное множество произвольных значений, которые дадут бесчисленное множество решений. Если все свободные неизвестные

435

приравнять к нулю, то решение будет состоять из значений базисных неизвестных. Такое решение называется базисным.

Втеории линейного программирования существует теорема, которая утверждает, что среди базисных решений системы можно найти оптимальное, а в некоторых случаях и несколько оптимальных решений, но все они обеспечат экстремум целевой функции. Таким образом, если найти какой-либо базисный план, а затем улучшить его, то получится оптимальное решение. На этом принципе и построен симплекс-метод.

Одним из модификаций симплекс-метода является улучшенный симплекс-метод. В литературе этот метод встречается также под названием метода обратной матрицы или модифицированного симплекс-метода.

При решении задач линейного программирования, в которых n (количество переменных) существенно больше m (количество ограничений), улучшенный симплекс-метод требует по сравнению с другими значительно меньшего количества вычислительных операций и объема памяти ЭВМ.

Вулучшенном симплекс-методе реализуется та же основная идея, что и

вобычном симплекс-методе, но здесь на каждой итерации пересчитывается не вся матрица A-1, обратная матрице ограничений A, а лишь та часть, которая относится к текущему базису Ax.

Симплекс метод в Excel

Так как при решении задач симплекс методом, приходится выполнять значительный объем вычислений, то большое значение придается эффективности и удобству их реализации на ЭВМ. Разработано немало программ по реализации задач симплекс методом на ЭВМ. Но самым оптимальным, представляется использование офисной программы MS EXCEL.

В MS EXCEL реализованы приближенные методы их решения с достаточно высокой степенью точности. Оценить получаемые решений можно посредством сравнения аналитических и алгоритмических решений отдельных практических задач.

Алгоритм симплекс метода и MS EXCEL удачно сочетаются друг с другом: и то, и другое основано на таблицах.

Каждый, у кого на компьютере установлен MS EXCEL, может с легкостью решать на нем задачи симплекс методом. Причем для этого не нужно ничего скачивать или устанавливать. Нужно только знать условие задачи и знать, как его ввести в MS EXCEL.

Мощным средством анализа данных MS EXCEL является надстройка Solver (Поиск решения). С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором

436

полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.

Программа Поиск решений (в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS EXCEL, которая предназначена для решения определенных систем уравнений, как линейных, так и нелинейных задач оптимизации, используется с 1991 года.

Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями:

количество неизвестных (decision variable) – 200;

количество формульных ограничений (explicit constraint) на неизвестные – 100;

количество предельных условий (simple constraint) на неизвестные –

400.

Разработчик программы Solver компания Frontline System уже давно специализируется на разработке мощных и удобных способов оптимизации, встроенных в среду популярных табличных процессоров разнообразных фирм-производителей (MS Excel Solver, Adobe Quattro Pro, Lotus 1-2-3).

Высокая эффективность их применения объясняется интеграцией программы оптимизации и табличного бизнес-документа. Благодаря мировой популярности табличного процессора MS EXCEL, встроенная в его среду программа Solver, есть наиболее распространенный инструмент для поиска оптимальных решений в сфере современного бизнеса.

Преимущества улучшенного симплекс метода

Улучшенный симплекс-метод, обладает значительными преимуществами по сравнению со стандартной формой. Это относится к точности, скорости и требованиям к памяти. Большая часть этих преимуществ определяется тем фактором, что, как правило, матрицы больших линейных задач (то есть с n>m>100) являются слабозаполненными, содержат малый процент ненулевых элементов.

Обычной является плотность 5% или менее. Улучшенная форма симплекс-метода в большей степени способна использовать преимущества, вытекающие из этого факта. В этой форме характеристические разности и ведущий вектор вычисляются непосредственно по исходным данным. Поскольку исходная матрица слабозаполнена, а перемножение следует производить только тогда, когда оба сомножителя отличны от нуля, то время вычислений значительно сокращается.

В дополнение к этому использование только исходных данных приводит к тому, что уменьшается возможность накопления ошибок округления. Наоборот, стандартные симплексные таблицы, даже если они первоначально являются слабозаполненными, в ходе итеративного процесса быстро заполняются ненулевыми элементами. Таким образом, время вычислений увеличивается, и, поскольку каждая таблица вычисляется из предшествующей, накопление ошибок может начать играть более серьезную роль.

437

Литература

1.Банди Б. Методы оптимизации. Вводный курс -М.. Радио и связь, 1988.- 128 с.

2.Гаас С. Линейное программирование.- М… ГИМФМЛ, 1961-304 с.

3.Гилл Ф., Мюррей У., Райт М. Практическая оптимиация. - М.. Мир, 1985.- 512 с.

4.Заславский Ю.Л. Сборник задач по линейному программированию.- М..

Наука, 1969.- 256 с.

5.Калихман И.Л. Сборник задач по линейной алгебре и программированию.- М.. Высшая школа, 1969.-160 с.

6.Калихман И.Л. Сборник задач по математическому программированию. Изд. 2-е, доп. И перераб. М., “Высшая школа”, 1975.-270 с.

7.Шапкин А.С., Мазаева Н.П. Математичаские методы и модели исследования операций: Учебник.- М.. Издательско-торговая корпорация

“Дашков и К°”, 2003.

438

НАУКА ГЛАЗАМИ МОЛОДЕЖИ

Сборник научных статей студентов вузов, ссузов и учащихся общеобразовательных учреждений

Компьютерная верстка – Очеповский А.В., Кириллова А.В.

Дизайн обложки – О. Крамар

Формат 60x84 1/16. Бумага офсетная. Гарнитура Arial, Romic. Печать оперативная. Подписано в печать 28.02.2011.

Усл. п.л. 19,94. Тираж 500 экз. Заказ № 164.

ООО «Издательство АсГард» член Ассоциации книгоиздателей России

443023, г. Самара, ул. Промышленности, 278 Тел./факс (846) 246-97-01, e-mail: as_gard@mail.ru

439