
- •Федеральное агентство по образованию
- •Содержание:
- •Программа курса
- •Неотрицательные матрицы в экономике и линейные экономические модели
- •Темы практических занятий.
- •Формы контроля
- •Вопросы к экзамену
- •1. Комплексные числа. Комбинаторика. Бином ньютона. Комплексные числа
- •Комбинаторика
- •Бином ньютона
- •2. Многочлены
- •Индивидуальное задание №1
- •5. Выделить целую и дробную часть рациональной функции:
- •6. Разложить на линейные множители в с и неприводимые (линейные и квадратичные) множители в r. Сделать проверку.
- •3. Матрицы. Определители. Матрицы
- •Определители.
- •4.Обратная матрица. Ранг матрицы. Линейная зависимость векторов.
- •5. Системы линейных уравнений.
- •Индивидуальное задание №2
- •Линейные пространства
- •7. Базис. Матрицы перехода. Процесс ортогонализации.
- •8. Матрицы операторов. Квадратичные формы. Матрицы операторов
- •Квадратичные формы
- •9. Число и вектор фробениуса. Продуктивность матриц.
- •10. Векторы. Скалярное произведение. Векторы
- •Скалярное произведение
- •11. Векторное и смешанное произведение векторов векторное произведение векторов
- •Смешанное произведение векторов
- •12. Уравнения прямой на плоскости
- •13. Уравнение плоскости. Уравнения прямой в пространстве.
- •14. Кривые второго порядка
- •Глава 5. Системы линейных уравнений.
- •Глава 6.
- •Глава 8.
- •Глава 14. Кривые второго порядка
- •Матричная алгебра в экономике Качаева Татьяна Ивановна
- •660041 Г. Красноярск, пр. Свободный, 79.
Индивидуальное задание №1
Выполнить действия в алгебраической форме. Результат записать в тригонометрической и показательной формах.
1.
![]() 16.
16.![]()
2.![]() 17.
17.![]()
![]()
3.![]() 18.
18.![]()
4.![]() 19.
19.![]()
5. ![]() 20.
20.
![]()
6. ![]() 21.
21. ![]()
7.
![]() 22.
22.
![]()
8.
![]() 23.
23.
![]()
9.
![]() 24.
24.![]()
10.
![]() 25.
25.
![]()
11.
![]() 26.
26.![]()
12.
![]() 27.
27.
![]()
13.
![]() 28.
28.![]()
14.
![]() 29.
29.![]()
15.
![]() 30.
30.![]()
Вычислить по формулам Муавра.
1.
![]() ,
,![]() 2.
2.![]() ,
,![]()
3.
![]() ,
,![]() 4.
4.![]() ,
,![]()
5.
![]() ,
,![]() 6.
6.![]() ,
,![]()
7.
![]() ,
,![]() 8.
8.![]() ,
,![]()
9.
![]() ,
,![]() 10.
10.![]() ,
,![]()
11.
![]() ,
,![]() 12.
12.![]() ,
,![]()
13.
![]() ,
,![]() 14.
14.![]() ,
,![]()
15.
![]() ,
,![]() 16.
16.![]() ,
,![]()
17.
![]() ,
,![]() 18.
18.![]() ,
,![]()
19.
![]() ,
,![]() 20.
20.![]() ,
,![]()
21.
![]() ,
,![]() 22.
22.![]() ,
,![]()
23.
![]() ,
,![]() 24.
24.![]() ,
,![]()
25.
![]() ,
,![]() 26.
26.![]() ,
,![]()
27.
![]() ,
,![]() 28.
28.![]() ,
,![]()
29.![]() ,
,![]() 30.
30.![]() ,
,![]()
Выразить sin4![]() и cos4
и cos4![]() через sin
через sin![]() и cos
и cos![]() ,
используя формулы Муавра и бином Ньютона.
,
используя формулы Муавра и бином Ньютона.
Найти разложение по биному Ньютона
1.
![]() ,
,![]() 2.
2.![]() ,
,![]()
3.
![]() ,
,![]() 4.
4.![]() ,
,![]()
5.
![]() ,
,![]() 6.
6.![]() ,
,
![]()
7.
![]() ,
, ![]() 8.
8.![]() ,
,
![]()
9.
![]() ,
,![]() 10.
10.![]() ,
,
![]()
11.
![]() ,
,![]() 12.
12.![]() ,
,
![]()
13.
![]() ,
,![]() 14.
14.![]() ,
,
![]()
15.
![]() ,
,![]() 16.
16.![]() ,
,
![]()
17.
![]() ,
,![]() 18.
18.![]() ,
,
![]()
19.
![]() ,
,![]() 20.
20.![]() ,
,
![]()
21.
![]() ,
,![]() 22.
22.![]() ,
,
![]()
23.
![]() ,
,![]() 24.
24.![]() ,
,![]()
25.
![]() ,
,![]() 26.
26.![]() ,
,![]()
27.
![]() ,
,![]() 28.
28.![]() ,
,![]()
29.
![]() ,
,![]() 30.
30.![]() ,
,![]()
4. Разделить многочлен f(x)
на многочлен х-![]() по схеме Горнера
по схеме Горнера
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
5. Выделить целую и дробную часть рациональной функции:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.![]()
7.
![]() 8.
8.![]()
9.
![]() 10.
10.![]()
11.
![]() 12.
12.![]()
13.
![]() 14.
14.![]()
15.
![]() 16.
16.![]()
17.
![]() 18.
18.![]()
19.
![]() 20.
20.![]()
21.
![]() 22.
22.![]()
23.
![]() 24.
24.![]()
25.
![]() 26.
26.![]()
27.
![]() 28.
28.![]()
29.
![]() 30.
30.![]()
6. Разложить на линейные множители в с и неприводимые (линейные и квадратичные) множители в r. Сделать проверку.
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
5.
![]()
![]()
6.
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
![]()
![]()
10.
![]()
![]()
11.
![]()
![]()
12.
![]()
![]()
13.
![]()
![]()
14.
![]()
![]()
15.
![]()
![]()
16.
![]()
![]()
17.
![]()
![]()
18.
![]()
![]()
19.
![]()
![]()
20.
![]()
![]()
21.
![]()
![]()
22.
![]()
![]()
23.
![]()
![]()
24.
![]()
![]()
25.
![]()
![]()
26.
![]()
![]()
27.
![]()
![]()
28.
![]()
![]()
29.
![]()
![]()
30.
![]()
![]()
3. Матрицы. Определители. Матрицы
3.1. Вычислить:
1)
![]() 2)
2)![]()
3.2. Вычислить:
1)
 2)
2)![]()
3)
![]() 4)
4)
3.3. Матрица А имеет размер![]() ,
матрицаС– размера
,
матрицаС– размера![]() .
Существует ли произведение
.
Существует ли произведение![]() ?
Каковы размеры матрицBиABC?
?
Каковы размеры матрицBиABC?
3.4. Проверить существует ли произведение матриц, если да, то вычислить его.
1)
 2)
2)
3)
 4)
4)
3.5. Протранспонировать матрицу:
1)
![]() 2)
2) 3)
3) 4)
4)
3.6. Всегда ли верно матричное тождество
![]() .
Привести примеры перестановочных
матриц.
.
Привести примеры перестановочных
матриц.
3.7. Вычислить
![]() ,
если
,
если
1)
![]() ,
,![]()
2)
![]() ,
,
3.8. Вычислить
![]() .
.
1)
 ,
2)
,
2)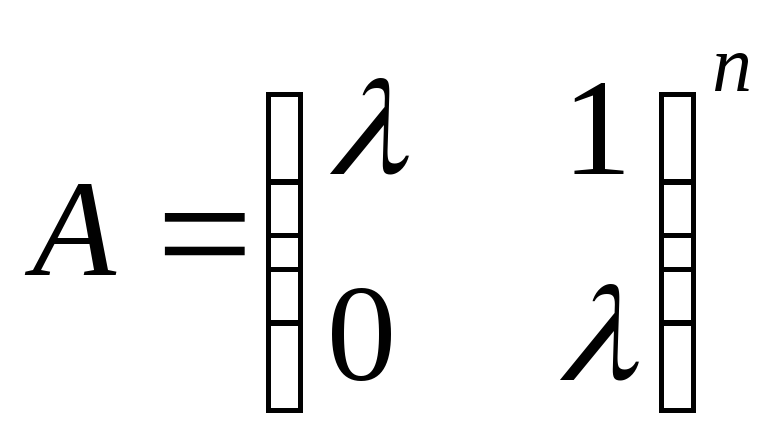 ,
,
3)
 ,
4)
,
4) ,
,
5)
 ,
6)
,
6) .
.
3.9. Найти все матрицы, перестановочные с матрицей
1)
 ,
2)
,
2) .
.
3.10. Найти обратные матрицы для
1)
 ,
2)
,
2) .
.
3.11. «Следом» квадратной матрицы называется
сумма элементов главной диагонали.
Доказать, что след
![]() равен следу
равен следу![]() .
.
Определители.
3.12. Вычислить определители
1)
![]() ,
2)
,
2)![]() ,
,
3)
 ,
4)
,
4) ,
,
5)
 ,
6)
,
6) .
.
3.13. Доказать, что для равенства нулю определителя второго порядка, необходимо и достаточно, чтобы его строки были пропорциональны. (коэффициент пропорциональности может быть равен 0).
3.14. Вычислить:
1) 2)
2) 3)
3)
4)
 5)
5) 6)
6)
7)
 8)
8) .
.
3.15. Доказать, что определитель диагональной матрицы равен произведению диагональных элементов.
3.16. Используя свойства определителя, доказать тождества:
1)
2)
3) Числа 19, 38 делятся на 19. Не вычисляя
определителя, докажите, что определитель
![]() делится на 19.
делится на 19.
3.17. Вычислить:
1) 2)
2) 3)
3)
4)
 5)
5) 6)
6)
7)
 8)
8) .
.
Вычислить 1) и 2) методом Гаусса.
