
- •Федеральное агентство по образованию
- •Содержание:
- •Программа курса
- •Неотрицательные матрицы в экономике и линейные экономические модели
- •Темы практических занятий.
- •Формы контроля
- •Вопросы к экзамену
- •1. Комплексные числа. Комбинаторика. Бином ньютона. Комплексные числа
- •Комбинаторика
- •Бином ньютона
- •2. Многочлены
- •Индивидуальное задание №1
- •5. Выделить целую и дробную часть рациональной функции:
- •6. Разложить на линейные множители в с и неприводимые (линейные и квадратичные) множители в r. Сделать проверку.
- •3. Матрицы. Определители. Матрицы
- •Определители.
- •4.Обратная матрица. Ранг матрицы. Линейная зависимость векторов.
- •5. Системы линейных уравнений.
- •Индивидуальное задание №2
- •Линейные пространства
- •7. Базис. Матрицы перехода. Процесс ортогонализации.
- •8. Матрицы операторов. Квадратичные формы. Матрицы операторов
- •Квадратичные формы
- •9. Число и вектор фробениуса. Продуктивность матриц.
- •10. Векторы. Скалярное произведение. Векторы
- •Скалярное произведение
- •11. Векторное и смешанное произведение векторов векторное произведение векторов
- •Смешанное произведение векторов
- •12. Уравнения прямой на плоскости
- •13. Уравнение плоскости. Уравнения прямой в пространстве.
- •14. Кривые второго порядка
- •Глава 5. Системы линейных уравнений.
- •Глава 6.
- •Глава 8.
- •Глава 14. Кривые второго порядка
- •Матричная алгебра в экономике Качаева Татьяна Ивановна
- •660041 Г. Красноярск, пр. Свободный, 79.
1. Комплексные числа. Комбинаторика. Бином ньютона. Комплексные числа
Выполнить действия:
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
1.2. Решить уравнения и проверить подстановкой корней в уравнение:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Представить в тригонометрической форме комплексные числа:
|
1. 1. |
8. –1. |
15.
|
|
2. 5. |
9.
|
16.
|
|
3. –2. |
10.
|
17.
|
|
4.
|
11.
|
18.
|
|
5.
|
12.
|
19.
|
|
6.
|
13.
|
20.
|
|
7.
|
14.
|
21.
|
Найти все значения корней:
|
1.
|
4.
|
7.
|
|
2.
|
5.
|
8.
|
|
3. |
6. |
9.
|
Вычислить:
|
1.
|
4.
|
7.
|
|
2.
|
5.
|
8.
|
|
3.
|
6.
|
9.
|
1) Доказать, что сумма и произведение взаимно сопряженных комплексных чисел являются действительными числами.
2) Доказать равенства:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
Найти формулы для вычисления степеней числа i.
Найдите: 1)
 ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.Как расположены на комплексной плоскости1) сопряженные числа; 2) противоположные числа; 3) корни n-ой степени?
Решить уравнения:
|
1.
|
3.
|
5.
|
|
2.
|
4.
|
|
1.11.Решить уравнения:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Где находится точка zкомплексной плоскости, если точка
 принадлежит
мнимой оси?
принадлежит
мнимой оси?Найти действительные корни уравнения

Комбинаторика
Найдите: 1) 0!; 2) 5!; 3) 7!; 4)
 ;5)
;5) .
.Сократите дробь: 1)
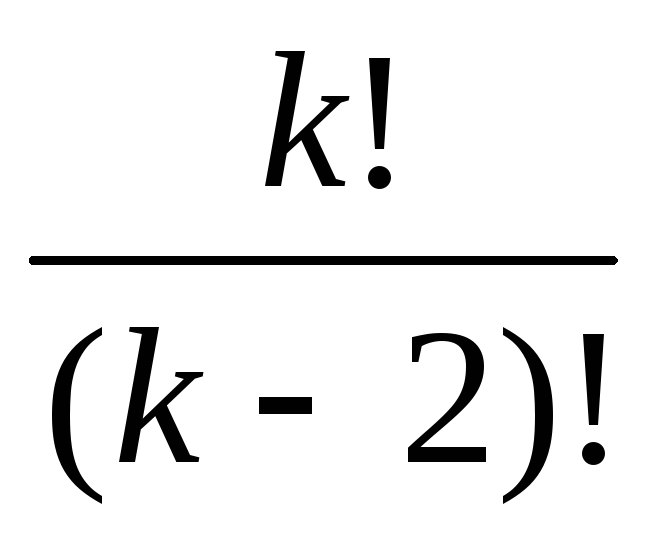 ;
2)
;
2) .
.Решить уравнение:

Найдите: 1)
 ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) ;
5)
;
5) .
.Докажите, что
 .
.Докажите равенство:
1.
![]() ;
2.
;
2.![]() .
.
Докажите, что
 .
.В некотором царстве все люди отличаются набором зубов. Каково население этого царства?
Бином ньютона
Разложите по биному:
1.
![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]() ;
5.
;
5.![]() ;
6.
;
6.![]() .
.
1.24. Найдите: 1) пятое; 2) 10; 3) 15; 4) 16
слагаемое в разложении
![]() .
.
Докажите, что
1)
![]() ;
;
2) Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Пользуясь формулой Муавра и биномом Ньютона выразить через степени
 и
и следующие функции кратных углов:
следующие функции кратных углов:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
2. Многочлены
Разделить:
1.
![]() на
на![]() ;
;
2.
![]() на
на![]() ;
;
3.
![]() на
на![]() ;
;
4.
![]() на
на![]() ;
;
5.
![]() на
на![]() ;
;
6.
![]() на
на![]() .
.
Выделить целую и дробную часть рациональной функции:
1.
![]() ;
2.
;
2.![]() ;
;
3.
![]() ; 4.
; 4.![]() .
.
Решить уравнения:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]() ;
;
6.
![]()
Доказать, что целые корни алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.
Найти целые корни уравнений:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.![]()
Доказать, что каждый рациональный корень алгебраического уравнения с целыми коэффициентами представим в виде
 гдер- делитель свободного члена,q- делитель старшего
коэффициента уравнения
гдер- делитель свободного члена,q- делитель старшего
коэффициента уравнения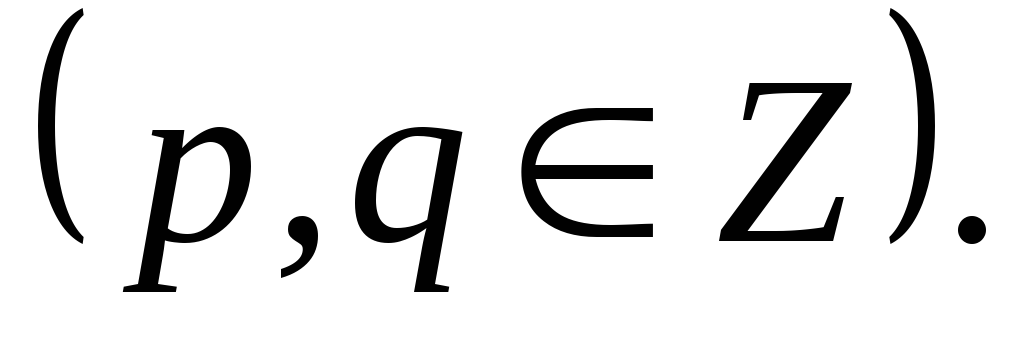
Найти рациональные корни уравнений:
1.
![]()
2.
![]()
2.8. Доказать, что если уравнение
![]() с действительными коэффициентами имеет
корень
с действительными коэффициентами имеет
корень![]() то
то![]() является тоже корнем этого уравнения.
является тоже корнем этого уравнения.
2.9. Доказать, что каждый многочлен нечетной степени с действительными коэффициентами имеет, по крайней мере, один действительный корень.
2.10. При каких значениях а и bчисло![]() является корнем уравнения
является корнем уравнения![]()
2.11. Определить кратность корня
![]()
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
2.12. Найти приведенный многочлен наименьшей степени с действительными коэффициентами, корнями которого являются:
1.
![]() и
и![]()
2.
![]() (корень кратности 2) и
(корень кратности 2) и![]()
2.13. Доказать, что если
![]() корни уравнения
корни уравнения![]() ,
то они связаны с коэффициентами уравнения
формулами Виета:
,
то они связаны с коэффициентами уравнения
формулами Виета:
![]()
![]()
![]()
……………………………………
![]() .
.
Уравнение

имеет корни


имеет корни


Найти третий корень уравнения.
2.15. Записать уравнение, корнями которого являются:
1.
![]()
![]()
![]()
![]()
2.
![]()
![]()
![]()
![]()
Представить многочлен в виде произведения линейных множителей:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
Представить многочлен в виде произведения неприводимых множителей с действительными коэффициентами:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
