
- •Федеральное агентство по образованию
- •Содержание:
- •Программа курса
- •Неотрицательные матрицы в экономике и линейные экономические модели
- •Темы практических занятий.
- •Формы контроля
- •Вопросы к экзамену
- •1. Комплексные числа. Комбинаторика. Бином ньютона. Комплексные числа
- •Комбинаторика
- •Бином ньютона
- •2. Многочлены
- •Индивидуальное задание №1
- •5. Выделить целую и дробную часть рациональной функции:
- •6. Разложить на линейные множители в с и неприводимые (линейные и квадратичные) множители в r. Сделать проверку.
- •3. Матрицы. Определители. Матрицы
- •Определители.
- •4.Обратная матрица. Ранг матрицы. Линейная зависимость векторов.
- •5. Системы линейных уравнений.
- •Индивидуальное задание №2
- •Линейные пространства
- •7. Базис. Матрицы перехода. Процесс ортогонализации.
- •8. Матрицы операторов. Квадратичные формы. Матрицы операторов
- •Квадратичные формы
- •9. Число и вектор фробениуса. Продуктивность матриц.
- •10. Векторы. Скалярное произведение. Векторы
- •Скалярное произведение
- •11. Векторное и смешанное произведение векторов векторное произведение векторов
- •Смешанное произведение векторов
- •12. Уравнения прямой на плоскости
- •13. Уравнение плоскости. Уравнения прямой в пространстве.
- •14. Кривые второго порядка
- •Глава 5. Системы линейных уравнений.
- •Глава 6.
- •Глава 8.
- •Глава 14. Кривые второго порядка
- •Матричная алгебра в экономике Качаева Татьяна Ивановна
- •660041 Г. Красноярск, пр. Свободный, 79.
Глава 5. Системы линейных уравнений.
5.1. 1) система совместна, х =1, у =1,z=1; 2) система совместна,x= -1,y= 0,z= 1;
3) система несовместна; 4) система
несовместна; 5) система совместна,
![]()
![]()
![]()
![]() 6) система совместна,
6) система совместна,![]()
![]()
![]()
![]()
5.2. 1) общее решение:![]() ,
,![]() ;
частное решение:
;
частное решение:![]() ;
;
ФСР:
![]() ,
,![]() ;
;
2) общее решение:
![]() ;
частное решение:
;
частное решение:![]() ;
ФСР:
;
ФСР:![]() ,
,![]() ,
,![]() ;
;
3) общее решение:
![]() ;
частное решение:
;
частное решение:![]() ;
ФСР:n–r= 3-1=2,
;
ФСР:n–r= 3-1=2,![]() ,
,![]() :
:![]() ;
;![]() ,
,![]() :
:![]() ,
,![]() ;
;
4) общее решение:
![]() ;
частное решение:
;
частное решение:![]() ;
ФСР:n–r= 3,
;
ФСР:n–r= 3,![]() ,
,![]() ,
,![]() :
:![]() ;
;![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ;
;![]() +
+![]() ;
;
5) общее решение:
![]() ;
частное решение:
;
частное решение:![]() ;
ФСР:n–r= 4,
;
ФСР:n–r= 4,![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() :
:![]() ;
;
![]() +
+![]() +
+![]() ;
;
6) общее решение:
![]() ;
частное решение:
;
частное решение:![]() ;
ФСР:n–r= 3-1=2,
;
ФСР:n–r= 3-1=2,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.3. 1) система совместная, неопределенная. Общее решение: х = (1, -С, С);
2) система совместная, неопределенная.
Общее решение:
![]() .
.
5.4. 1) определена,![]() ,r(А) = 3; 2) несовместна,
а= -3,
,r(А) = 3; 2) несовместна,
а= -3,![]() ;
;
3) неопределенна а= -3,
![]() .
.
5.5. 1) определена, при![]() ,
,![]() r(А) = 3; 2) несовместна,
при а= -2;
r(А) = 3; 2) несовместна,
при а= -2;
3) неопределенна, при а= 1.
Глава 6.
СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ.
ЛИНЕЙНЫЕ ПРОСТРАНСТВА.
6.1.1)
![]()
![]() ,
,![]()
![]() ,
,![]() ;
;
2)
![]()
![]() ,
,![]()
![]() ,
,![]() ;
;
3)
![]()
![]() ;
4)
;
4)
![]()
![]() ;
;
5)
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ;
;
6)
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ;
;
7)
![]()
![]() ,
,
![]() комплексные;
комплексные;
8)
![]()
![]() ;
;
![]()
![]() ;
;
9)
![]()
![]() ,
,
![]()
![]()
10)
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ;
;
11)
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ;
;
12)
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
6.2.

![]()
![]()
собственные значения равны диагональным элементам.
6.4.

по аналогии с 6.2.
![]()
6.5.
![]()
![]()
![]() .
.
6.6. 1) является; 2) не является; 3) не является; 4) является; 5) является; 6) является;
7) не является; 8) является; 9) является; 10) не является; 11) не является; 12) является;
13) является; 14) является; 15) является; 16) является; 17) не является; 18) является;
19) не является; 20) является.
Глава 7.
БАЗИС. МАТРИЦЫ ПЕРЕХОДА. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ.
7.1.1) ненулевой вектор, лежащий на прямой;
2) любые два неколлинеарных вектора на плоскости;
3) две матрицы, например
![]() и
и![]() ;
;
4) три многочлена, например 1, х,
![]() .
.
7.2. 1) базис состоит из![]() ;
2) базис состоит из
;
2) базис состоит из![]() .
.
7.3. 1) Х(1/3,1/3,1/3); 2)X(0,-5,4).
7.4. 1)f(t) = (5,2,-1,1); 2)f(t) = (4,2,-1,1); 3)f(t) = (5,2,-1,-5).
7.5. 1)
 , базис, например,
, базис, например,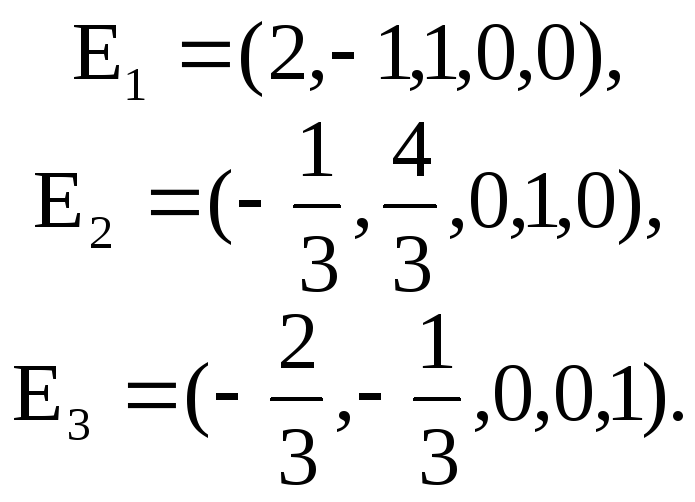
7.6. 1)![]() ;
2)
;
2) .
.
7.7. 1) ;
2)
;
2) .
.
7.8. 1) с = (2,2,1,0),d= (-5,2,6,1); 2) с = (1,-2,1,0),d= (17/6,-2/3,-25/6,1).
7.9. 1) один из векторов
![]() ;
;
2)
![]() ,
,
![]() .
.
7.10. Процессом ортогонализации
системы векторов![]() называется переход от этой системы к
новой системе
называется переход от этой системы к
новой системе![]() ,
построенной следующим образом:
,
построенной следующим образом:![]()
![]() где
где![]() если
если![]() и
и![]() -
любое число, если
-
любое число, если![]() .
.
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() .
.
Глава 8.
МАТРИЦЫ ОПЕРАТОРОВ.
8.1.
![]() .8.2. 1)
.8.2. 1)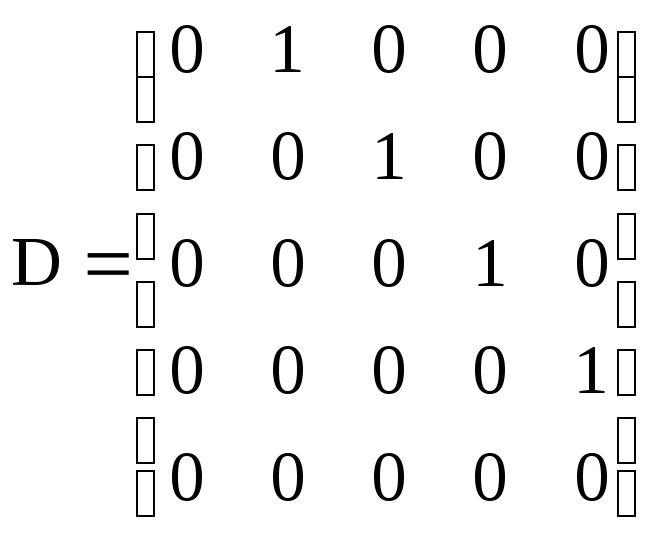 ;
2)
;
2) .
.
8.3. 1) ;
2)
;
2) ;
3)
;
3)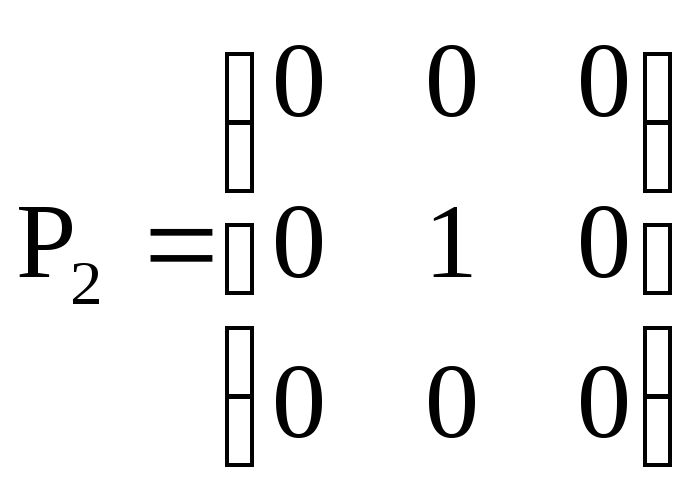 ;
4)
;
4) ;
;
5)
 .
.
КВАДРАТИЧНЫЕ ФОРМЫ.
8.5. 1)![]() ,
положительно определенная; 2)
,
положительно определенная; 2)![]() ,
знакопеременная;
,
знакопеременная;
3)
![]() ,
положительно определенная; 4)
,
положительно определенная; 4)![]() ,
знакопеременная;
,
знакопеременная;
5)
![]() ,
знакопеременная; 6)
,
знакопеременная; 6)![]() ,
знакопеременная;
,
знакопеременная;
7)
![]() ,
положительно определенная; 8)
,
положительно определенная; 8)![]() знакопеременная.
знакопеременная.
Глава 9.
ЧИСЛО И ВЕКТОР ФРОБЕНИУСА. ПРОДУКТИВНОСТЬ МАТРИЦ.
ЧИСЛО И ВЕКТОР ФРОБЕНИУСА.
9.1. 1)
![]()
![]() С > 0; 2)
С > 0; 2)![]()
![]() С > 0;
С > 0;
3)
![]()
![]() С > 0; 4)
С > 0; 4)![]()
![]() С > 0.
С > 0.
9.2.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() 4)
4)![]() .
.
ПРОДУКТИВНОСТЬ МАТРИЦ.
9.3. 1) да; 2) да; 3) да; 4) нет; 5) да.
9.4.
1)
![]() ; 2)
; 2)![]() .
.
9.5. 1)
![]() ;
2)
;
2)![]()
Глава 10.
ВЕКТОРЫ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ.
ВЕКТОРЫ.
10.1. 1)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
3)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.2. 1)
да; 2) нет. 10.3.
М(3,3,3).
10.5.
![]() .
10.6.
.
10.6.
![]() .
.
10.7. 1)
векторы коллинеарны. Вектор
![]() длиннее
длиннее
![]() в 3 раза. Векторы противоположно
направлены;
в 3 раза. Векторы противоположно
направлены;
2) векторы коллинеарны.
Вектор
![]() длиннее
длиннее![]() в 3 раза. Векторы сонаправлены.
в 3 раза. Векторы сонаправлены.
10.9.
![]() .10.10.
.10.10.
![]() ,
,![]() ,
,![]() .
.
10.12.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ.
10.13. 1) – 3; 2) 4; 3) 7; 4) 19; 5) -49; 6) -95.
10.14. Геометрический смысл: сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
10.15. Векторы
![]() и
и![]() коллинеарны.
коллинеарны.
10.16. 1)
-1,5; 2) -1,5. 10.17.
![]() ,
,![]() .
.
10.18.
![]()
![]() .
10.20. 1)
5; 2) 21; 3) 33; 4) 13; 5) 13; 6) 58; 7) -13.
.
10.20. 1)
5; 2) 21; 3) 33; 4) 13; 5) 13; 6) 58; 7) -13.
10. 21.
![]() .10.22.
.10.22.
![]() .
10.23.
.
10.23.
![]() .
10.24.
.
10.24.
![]() .
.
10.25.
![]() .
.
Глава 11.
ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
11.1. 16.11.2. 12![]() .11.3. 1) 24; 2) 36.11.4. 1) 3; 2) 75;
3) 192.
.11.3. 1) 24; 2) 36.11.4. 1) 3; 2) 75;
3) 192.
11.5. Векторы
![]() и
и![]() должны быть коллинеарны.
должны быть коллинеарны.
11.8. 1) (5,1,7); 2) (-5,-1,-7); 3) (10, 2,14); 4) (20,4, 28).
1.9. 1) 0; 2) (-12, 8, 12); 3) (-6, 4, 6).11.10. 14.11.11. 25.
11.12.
![]() .11.13.
.11.13.
![]() .11.14.
-91.
.11.14.
-91.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
11.15. 1) правая; 2) левая; 3) левая; 4) правая; 5) левая; 6) левая.11.16. 24.11.20. -7.11.21.1) компланарны; 2) не компланарны; 3) компланарны.11.23. 11.
Глава 12.
УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ.
12.1. (3;-5).12.2. 2х+3у-7=0; 3х-2у-4=0.12.3.
![]() .12.4. Q(11;-11).
.12.4. Q(11;-11).
12.5. 2х+5у-29=0.12.6. 1) х+у-5=0; 2) 4х+3у-11=0; 3) х+у+2=0.12.7. М(3,4).
12.8. 4х+у-3=0.12.11. у= - 5х +3; у=![]() .12.12. РК: 11х-у-28=0.12.13. К(-12;5).
.12.12. РК: 11х-у-28=0.12.13. К(-12;5).
12.14. М(10,-5).12.15. 1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
12.18.1) пересекаются в точке М (-5/11;7/11); 2) не пересекаются в одной точке.
12.19. 8х+4у-5=0.12.20.
![]() .
.
Глава 13.
УРАВНЕНИЕ ПЛОСКОСТИ. УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ.
13.1. х –у -3z+2=0.13.2. х +4у +7z+16=0.13.3. 3х+3у+z-8=0.
13.4. 1) параллельны; 2) перпендикулярны; 3) пересекаются; 4) пересекаются;
5) пересекаются; 6) пересекаются.
13.5. х +2z- 4=0.13.6. А(1,-2,2).13.9. 1) 2; 2) 3,5; 3) 6,5.
13.10. 1) 4х -5у +z-2=0; 2) 6х +2у -4z-2=0.13.11. -5х -5у+5z-10=0.
13.12. х +19у -7z+57=0.
13.13. 1) (х-2)/4=(у +1)/14=z/8; 2)x/(-5)=y/12=(z-2,5)/17; 3) (x+1)/5=y/10=z/5.
13.14. 1) не параллельны, не перпендикулярны; 2) перпендикулярны;
3) не параллельны, не перпендикулярны. 13.15. 4/21.13.19. A(2,-3,6).
13.20. P(3,-2,4).13.21. (1,4,-7).13.22. 7.13.23. 1) 13; 2) 3.
