2. Геометрический смысл неопределенного интеграла

Рассмотрим пример

∫xdx =+ С - совокупность первообразных для функцииf(x) = х.

Графически это семейство парабол:

С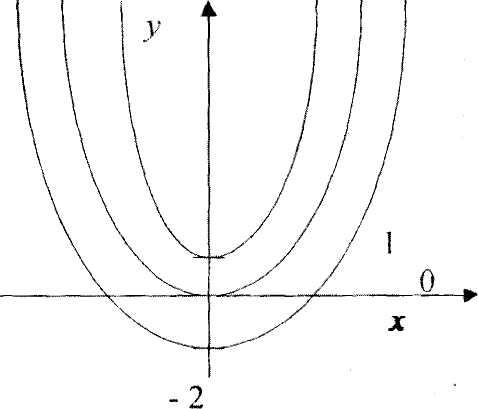= 0

С = 1

С = -2 …

Аналогично, неопределенный интеграл ∫f(x)dx представляет собой семейство кривых у = F(x) + С, каждая из которых может быть

получена путём параллельного переноса другой вдоль оси OY. Эти кривые называются интегральными кривыми. Все кривые данного семейства обладают общим свойством: если провести касательные в точках с одинаковой абсциссой х = х₀, то эти касательные будут параллельны. Действительно, их угловые коэффициенты равны

[F(x) + С]'=F'(x) │=f(x₀).

3. Свойства неопределенного интеграла

1°. Производная от неопределенного интеграла равна подинтегральной функции

(3)

Доказательство.

,

что и требовалось доказать.

2°. Дифференциал от неопределенного интеграла равен подинтегральному выражению

(4)

Доказательство.

,

что и требовалось доказать.

3°. Неопределенный интеграл от дифференциала некоторой функции

равен этой функции плюс произвольная постоянная

(5)

Доказательство. Возьмем дифференциалы от левой и правой части равенства (5)

и

Следовательно, сами выражения могут отличаться только на постоянную, и равенство (5) доказано.

4°. Постоянный множитель можно выносить за знак интеграла

(6)

Доказательство. Найдем производные от левой и правой части равенства (6).

(∫а f(x)dx)'= a f(x)

(a ∫ f(x)dx)' = a( ∫ f(x)dx)' = a f(x)

Следовательно, сами выражения могут отличаться только константой, и равенство (6) доказано.

5°. Неопределённый интеграл от алгебраической суммы двух или нескольких интегральных функции равен алгебраической сумме их интегралов.

(7)

Доказательство. Найдем производные от обеих частей данного равенства

Таким образом, иявляются

первообразными одной и той же функции f₁ (х)+f₂(х), но тогда они отличаются друг от друга на некоторую постоянную, т. е. любая функция, стоящая в левой части (7) отличается от функции в правой части на константу и равенство (7) доказано.

6°. Инвариантность формул интегрирования

Теорема. Пусть ∫f(x)dx = F(x) + С и и = φ(х) - любая функция, имеющая непрерывную производную. Тогда

∫f(u)du = F(u) + С (8)

Доказательство. Имеем F'(x) =f(x). Возьмём сложную функцию

F(u) =F(φ(x)). В силу теоремы об инвариантности дифференциала 1-го порядка имеем

dF(u) = F'(и) du = f(u)du

Отсюда

∫dF(u) = F'(u)du = ∫f(u)du = F(u) + С,

что и требовалось доказать.

Например:

4. Таблица интегралов

Таблица интегралов получается из таблицы производных. Каждая из формул легко проверяется дифференцированием.

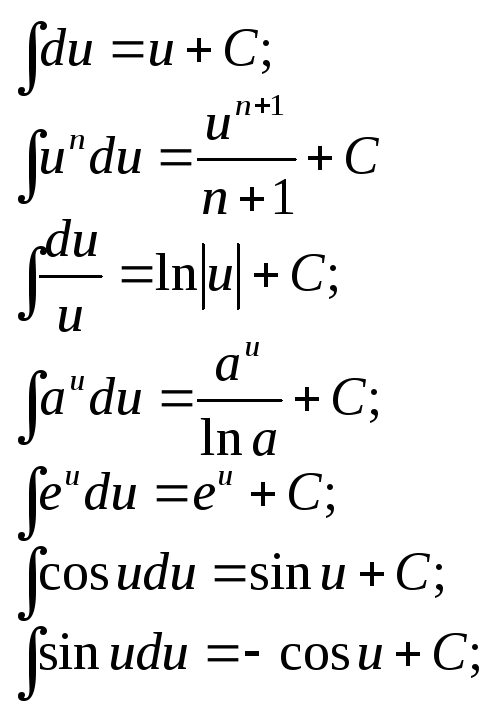
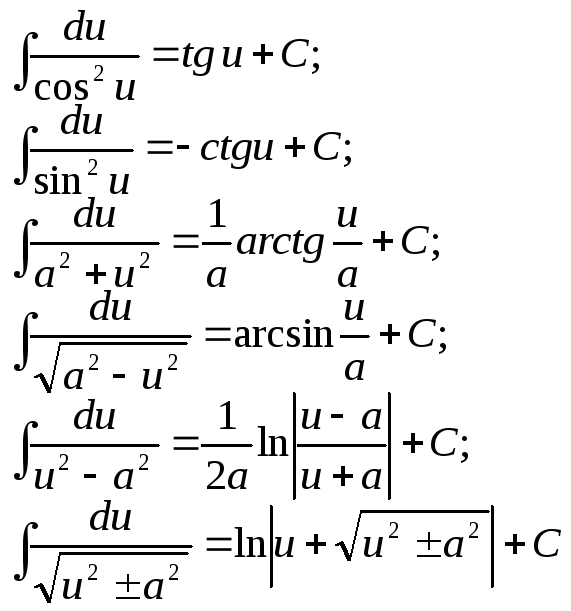
1. 8.

2. 9.

3. 10.

4. 11.

5.

12.

6

.

7. 13.

Докажем, например, формулу 8

Для этого возьмем производную от правой части и сравним результат с подинтегральной функцией

,

что и требовалось доказать.

Аналогично докажем формулу 11:

Замечание: Если операция дифференцирования элементарных функций снова приводит к элементарной функции, то операция интегрирования уже может привести к неэлементарным функциям.

Например:

- интеграл Пуассона,

- интегралы Френеля

- интегральный логарифм,

- интегральный косинус,

- интегральный синус

Такие интегралы представимы в виде суммы степенного ряда.

На­пример: