
- •Глава IX Определённый интеграл
- •1. Конструкция определенного интеграла
- •Свойства определенного интеграла
- •П 11. Дифференцирование определенного интеграла по верхнему (нижнему) пределу. Формула Ньютона-Лейбница
- •П 12. Замена переменной в определенном интеграле
- •П 13. Интегрирование по частям в определенном интеграле
- •П 14. Вычисление площадей плоских фигур
- •14.1. Вычисление площадей плоских фигур в декартовых координатах
- •14.2. Вычисление площадей плоских фигур в полярных координатах
- •П 15. Вычисление длины кривой
- •П 16. Несобственный интеграл первого рода. Критерий Коши. Признаки сравнения.
- •П 17. Условная сходимость несобственного интеграла. Признак Абеля-Дирихле.
- •§11. Несобственный интеграл и ряд. Интегральный признак Коши сходимости ряда.
- •§12. Несобственный интеграл второго рода.
- •П 18. Главное значение несобственного интеграла.
П 17. Условная сходимость несобственного интеграла. Признак Абеля-Дирихле.
Пусть
ф-я f(x)
интегрируема по Риману на любом конечном
отрезке [a,
x].
Несобственный интеграл
![]() называется абсолютно сходящимся, если
сходится интеграл
называется абсолютно сходящимся, если
сходится интеграл![]() ,
и условно сходящимся, если интеграл
,
и условно сходящимся, если интеграл![]() расходится, а сам интеграл
расходится, а сам интеграл![]() сходится.
сходится.
Теорема 1.Абсолютно сходящийся интеграл сходится.
Док-во.
Пусть
![]() сходится. Тогда по критерию Коши
сходится. Тогда по критерию Коши <ε
для
<ε
для Vε>0
и для Vx’,
x”>A(ε).
Согласно свойствам интеграла (см §4)
 ≤
≤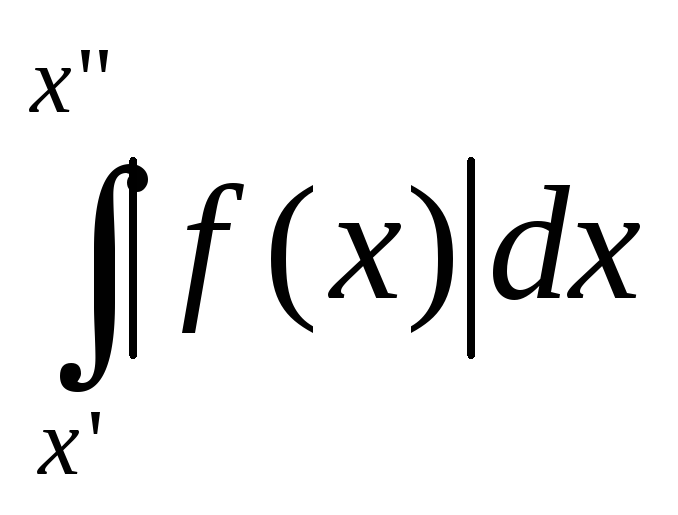 .=>
.=> <ε,
т.е. выполняется критерий Коши для
данного интеграла
<ε,
т.е. выполняется критерий Коши для
данного интеграла
![]() ,
=> он сходится. Теорема доказана.
,
=> он сходится. Теорема доказана.
Замечание 1. Признаки сравнения, рассмотренные в предыдущем параграфе, можно применить для исследования интегралов на абсолютную сходимость.
Пример
1. Исследовать
на абсолютную сходимость интеграл
![]()
Решение.
![]() ≤
≤![]() ,
а интеграл
,
а интеграл![]() сходится, то по признаку сравнения
данный интеграл сходится абсолютно.
сходится, то по признаку сравнения
данный интеграл сходится абсолютно.
Теорема 2.(Абеля-Дирихле). Если
1)функция непрерывна на полуинтервале [a, ∞] и имеет на нем ограниченную первообразную F(x);
2)функция
g(x)
монотонно убывает, стремится к 0 при
x→+∞
и имеет непрерывную производную g’(x),
то несобственный интеграл
![]() сходится.
сходится.
Док-во.
Покольку функции f(x),
g(x),
f(x)g(x)
непрерывны на [0, ∞), то они интегрируемы
на любом конечном отрезке [a,
x].
Рассмотим интеграл
 (x’<x”≥a)
и проинтегрируем его по частям.
(x’<x”≥a)
и проинтегрируем его по частям.
 =
= =g(x)F(x)
=g(x)F(x)
 -
- .(1)
.(1)
По
условию теоремы
![]() ≤M.
Поскольку g(x)→0
при x→+∞
монотонно убывает, то g(x)>0,
а g’(x)<0.
Из (1) получим
≤M.
Поскольку g(x)→0
при x→+∞
монотонно убывает, то g(x)>0,
а g’(x)<0.
Из (1) получим
 ≤
≤![]()
 +
+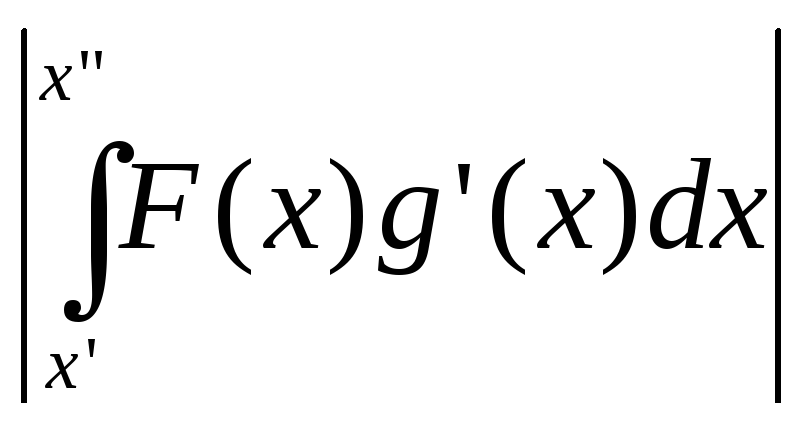 ≤M(g(x’)-g(x”))+M
≤M(g(x’)-g(x”))+M =2M(g(x’)-g(x”)). (2)
=2M(g(x’)-g(x”)). (2)
Т.к.
g(x)→0
при x→+∞,
то по критерию Коши g(x’)-g(x”)<ε/2
для Vε>0
и для Vx’,
x”>A(ε),
т.е. выполняется критерий Коши сходимости
несобственного интеграла
![]() .
Теорема доказана.
.
Теорема доказана.
Пример
2. Исследовать
на сходимость интеграл
![]() .
.
Решение.
Доопределим подынтегральную функцию,
т.е. положим
![]() =1,
и представим данный интеграл в виде
суммы двух интегралов
=1,
и представим данный интеграл в виде
суммы двух интегралов
![]() =
=![]() +
+![]() .
.
Поскольку
1-й интеграл (собственный) существует,
то следует исследовать на сходимость
только 2-й интеграл. По признаку
Абеля-Дирихле интеграл
![]() сходится, следовательно сходится и
данный интеграл
сходится, следовательно сходится и
данный интеграл![]() .
Позже мы докажем, что
.
Позже мы докажем, что
![]() =π/2. (3)
=π/2. (3)
Покажем
теперь, что интеграл
![]() расходится. Действительно,
расходится. Действительно,![]() ≥
≥![]() =
=![]() (1-cos2x).
Тогда
(1-cos2x).
Тогда
![]() ≥
≥![]()
![]() =
=![]()
![]() -
-![]()
![]() .(4)
.(4)
Интеграл
![]() расходится и равен +∞. Интеграл
расходится и равен +∞. Интеграл![]() сходится по признаку Абеля-Дирихле.
Поэтому переходя в (4) к пределу приx→+∞,
получим, что правая часть (а => и левая)
неравенства →∞. =>, интеграл
сходится по признаку Абеля-Дирихле.
Поэтому переходя в (4) к пределу приx→+∞,
получим, что правая часть (а => и левая)
неравенства →∞. =>, интеграл
![]() расходится, а вместе с ним расходится
и интеграл
расходится, а вместе с ним расходится
и интеграл![]() .
.
Вывод:
интеграл
![]() условно сходящийся.
условно сходящийся.
Замечание
2. Из
сходимости интеграла
![]() следует сходимость интеграла
следует сходимость интеграла![]() для
дляVx≥0.
Этот интеграл определяет неэлементарную
функцию six=![]() ,
о которой говорилось ранее (см. §9 гл.
7).
,
о которой говорилось ранее (см. §9 гл.
7).
Пример
3. Исследовать
на сходимость интеграл Френеля
![]() .
.
Решение.
![]() =
=![]() +
+![]() =
=![]() +
+![]() .
=> интеграл сходится по признаку
Абеля-Дирихле.
.
=> интеграл сходится по признаку
Абеля-Дирихле.
Решение. Доказать, что интеграл Френеля сходится условно.
§11. Несобственный интеграл и ряд. Интегральный признак Коши сходимости ряда.
Между
несобственными интегралами 1-го рода
![]() и числовыми рядами
и числовыми рядами![]() сущесвует глубокая аналогия. Если
суммирование поn
заменить интегрированием по x,
то общему члену ряда
сущесвует глубокая аналогия. Если
суммирование поn
заменить интегрированием по x,
то общему члену ряда
![]() будет соответсвовать подынтегральная
функцияf(x).
Частичной сумме ряда
будет соответсвовать подынтегральная
функцияf(x).
Частичной сумме ряда
![]() -
собственный интеграл
-
собственный интеграл![]() .
Сумме ряда
.
Сумме ряда![]() -несобственный интеграл
-несобственный интеграл![]() .
Остатку ряда
.
Остатку ряда![]() =
=![]() -
интеграл
-
интеграл![]() .
.
Аналогичны
и признаки сходимости для рядов и
несобственных интегралов – критерий
Коши, признаки сравнения, признак
Абеля-Дирихле и др. Однако полной аналогии
нет. Например, нет аналога необходимому
признаку сходимости ряда – если ряд
![]() сходится, то
сходится, то![]() →0
приn→∞.
Если интеграл
→0
приn→∞.
Если интеграл
![]() сходится, тоf(x)
может и не →0. Например, интеграл Френеля
сходится, тоf(x)
может и не →0. Например, интеграл Френеля
![]() сходится (см пр3 §10), но
сходится (см пр3 §10), но![]() не →0 приx→∞.
не →0 приx→∞.
По
определению несобственный интеграл
![]() сходится, если ф-яF(x)=
сходится, если ф-яF(x)=
![]() имеет предел приx→+∞,
если для любой б.б. последовательности
{
имеет предел приx→+∞,
если для любой б.б. последовательности
{![]() }
соответствующая последовательностьF(
}
соответствующая последовательностьF(![]() )=
)= сходится.
сходится.
С
другой стороны вопрос о пределе
последовательности F(![]() )
тождественен вопросу о сходимости ряда
)
тождественен вопросу о сходимости ряда
F(![]() )+(F(
)+(F(![]() )-F(
)-F(![]() ))+(F(
))+(F(![]() )-F(
)-F(![]() ))+…+(F(
))+…+(F(![]() )-F(
)-F(![]() ))+…=
))+…= =
=![]() ,
,
![]() ,
т.к. F(
,
т.к. F(![]() )-частичная
сумма этого ряда.
)-частичная
сумма этого ряда.
Все выше сказанное сформируем в виде след. теоремы.
Теорема
1. Для сущ.
Несобственного интеграла
![]() необходимо и достаточно, чтобы ряд
необходимо и достаточно, чтобы ряд
 ,
,
![]() ,
,![]() >a (1)
>a (1)
сходился
к одной и той же сумме при любом выборе
б.б. последовательности {![]() }.
Эта сумма и дает
значение
несобственного интеграла.
}.
Эта сумма и дает
значение
несобственного интеграла.
Замечание.
Если подынтегральная ф-я f(x)
неотрицательная на [a,
+∞), то для сущ. интеграла
![]() достаточно сходимости рядя (1) при одном
частном выборе б.б. последовательности
{
достаточно сходимости рядя (1) при одном
частном выборе б.б. последовательности
{![]() }.
Действительно, в этом случае ф-яF(x)=
}.
Действительно, в этом случае ф-яF(x)=![]() монотонно возрастающая, а последовательностьF(
монотонно возрастающая, а последовательностьF(![]() )
ограничена суммой ряда (1) и => имеет
предел.
)
ограничена суммой ряда (1) и => имеет
предел.
Поскольку для рядов известны многочисленные признаки сходимости, то иногда удобнее вопрос о сходимости несобственного интеграла свести к вопросу о сходимости ряда.
Пример
1. Исследовать
на сходимость интеграл
![]() ,
α, β>0.
,
α, β>0.
Решение. Если f(x)- интегральная ф-я, то при πn≤x≤π(n+1) имеем
![]() ≤f(x)≤
≤f(x)≤![]() .(2)
.(2)
Найдем
интеграл
![]() =
=![]() =
=![]() =
=![]() =
=![]() .
Интегрируя неравенство (2) в пределах
от πn
до π(n+1),
получим
.
Интегрируя неравенство (2) в пределах
от πn
до π(n+1),
получим
![]() ≤
≤![]() ≤
≤![]() . (3)
. (3)
Суммируя неравенство (3) по n от 0 до ∞, получим
 ≤
≤![]() ≤
≤ .
.
Оба
крайних рядя в последнем неравенстве
сходятся или расходятся одновременно
с рядом
![]() =
= (предельный признак сравнения), который
сходится при
(предельный признак сравнения), который
сходится при![]() и расходится при
и расходится при![]() .
При этих же условиях сходится или
расходится данный интеграл.
.
При этих же условиях сходится или
расходится данный интеграл.
Теорема
2. Если
подынтегральная ф-я f(x)
непрерывная, неотрицательная и монотонно
убывающая на [0, ∞), то несобственный
интеграл
![]() и ряд
и ряд![]() одновременно сходится или одновременно
расходится.
одновременно сходится или одновременно
расходится.
Док-во.
Пусть n≤x<n+1.
Поскольку ф-я f(x)
монотонно убывающая, то f(n+1)<f(x)≤f(n).
Интегрируя эти неравенства в пределах
от n
до n+1,
получим f(n+1)<![]() ≤f(n).
Суммируя по n
от 0 до ∞, получим
≤f(n).
Суммируя по n
от 0 до ∞, получим
![]() =
=![]() ≤
≤![]() ≤
≤![]() .
Эти неравенства доказывают теорему.
.
Эти неравенства доказывают теорему.
Теорема 2 носит название интегрального признака Коши сходимости ряда.
Пример
2. Исследовать
на сходимость ряд
![]() .
.
Решение.
Ф-я f(x)=![]() удовлетворяет требованиям теоремы 2 на
[3, ∞). Воспользуемся интегральным
признаком Коши.
удовлетворяет требованиям теоремы 2 на
[3, ∞). Воспользуемся интегральным
признаком Коши.
![]() =
=![]() =
=![]()
![]()
![]() =
=![]()
При
α=1
![]() =lnlnx
=lnlnx![]() -
расходится.
-
расходится.
Вывод: данный интеграл сходится при α>1 и расходится при α≤1.
