Глава IX Определённый интеграл

1. Конструкция определенного интеграла

Пусть функция определена на отрезке. Разобьем этот отрезок напроизвольных частей точками разбиения. В каждом из полученных отрезковвыберем произвольную точку. Черезобозначим длину отрезка. Обозначим сумму, которую назовем интегральной суммой Римана функциина отрезке, соответствующей данному разбиениюотрезкаи данному выбору точек.

Геометрический смысл интегральной суммы заключается в том, что это сумма площадей прямоугольников с основаниямии высотой(при выполнении условия).

Обозначим через длину наибольшего отрезка разбиения: .

Определение 1. Если существует конечный предел интегральной суммы прии при условии, что он не зависит от разбиенияотрезкаи от выбора точек, то этот предел называетсяопределенным интегралом Римана от функции на отрезкеи обозначается.

Другими словами, : . Нетрудно видеть, что мы дали определение интеграла Римана в духе определения предела по Коши.

Свойства определенного интеграла

Определенный интеграл обладает следующими свойствами:

1°.,

справедливость следует из определения .

2°. Если интегрируема наи, тоинтегрируема и на.

3°. (аддитивность), где.

Справедливо и обратное

.

Из свойства 3° следует интегрируемость кусочно-непрерывной на функции.

Оп р е д е л е н и е.Функция называется кусочно-непрерывной на отрезке,если она имеет на этом отрезке конечное число точек разрыва первого рода. При этом в точках разрывафункция может быть не определена, это значит, что в этих точках значение функции можно брать любым (конечным), и величина интеграла не меняется в этом случае.

4°. Если иинтегрируемы на, тотакже интегрируема наи при этом

(линейность)

5°.Если иинтегрируемы на, то и их произведениетоже интегрируемо на этом отрезке.

6°.Если на, то(следует из определения).

7°. Если и существует точкана, в которойнепрерывна и,

то (справедливость из определения и свойства непрерывной функции).

8°. , модуль интеграла не превосходит интеграла от модуля подынтегральной функции (справедливость следует из определения, из свойства модуля суммы и свойства предела последовательности).

9°. Пусть интегрируема наи. Тогда функции и непрерывны на.

–интеграл с переменным верхним пределом, ,

–интеграл с переменным нижним пределом, ,.

Т. к. интегрируема на, то она интегрируема и на, где.

.

.

, так как по условию .

называется непрерывной в точке ,при;

, значит при следует.

Непрерывность доказывается аналогично.

10°. Интегральная теорема о среднем

Т е о р е м а. Пусть функции иинтегрируемы на отрезке,ограничена, т. е., ане меняет свой знак, т. е.либо, тогда существует такое число,, что

Д о к а з а т е л ь с т в о. По условию, выполняется неравенство

.

Умножим (2) на , т. е.

(3)

Проинтегрируем неравенства (3)

.

(4)

Проанализируем (4)

1) если , то, значит (4) выполняется;

2)если , то

,

Так как , то полагаем

,

откуда получаем

.

(5)

Случай доказывается аналогично.

Если непрерывна на,, то функция принимает промежуточное значение, т.е. если, то существует такое, чтои

.

6

Если , то выражение (6) принимает вид

,

откуда

, .

Это можно истолковать геометрически следующим образом. Площадь криволинейной трапеции равна площади прямоугольника со стороной . Это и есть среднее значение.

y

x

0 a b
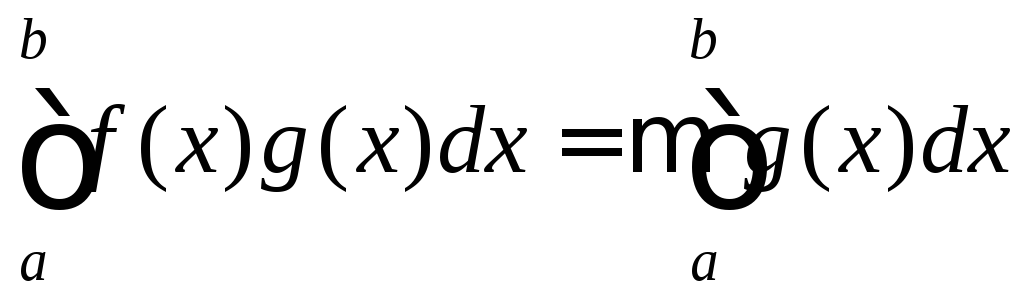
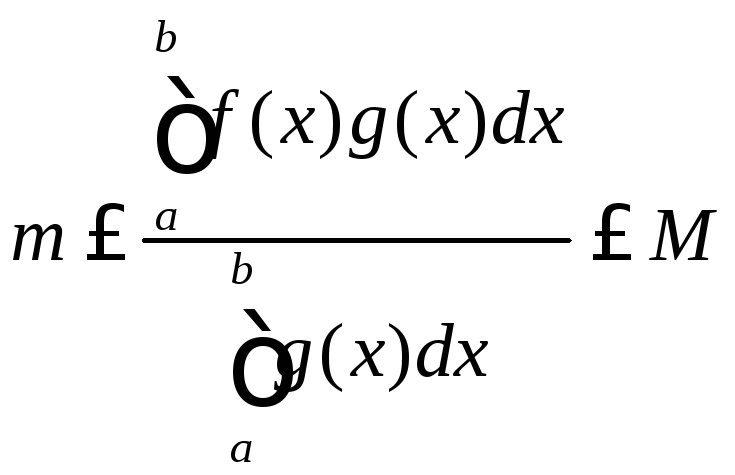