МЕТОДЫ ОПТИМИЗАЦИИ

8.1. ВВЕДЕНИЕ

Целочисленное линейное программирование (ЦЛП) ориентировано на решение задач линейного программирования, в которых все или некоторые переменные должны принимать целочисленные (или дискретные) значения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На сегодня не существует надежных вычислительных алгоритмов решения таких задач.

В настоящей главе рассматриваются сначала примеры задач целочисленного программирования, а затем методы их решения.

6.2. ПРИМЕРЫ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО

ПРОГРАММИРОВАНИЯ

Рассмотрим сначала простые практические задачи, которые сводятся к задачам ЦЛП, затем обратимся к более сложным. Для удобства задачи, в которых все переменные должны быть целочисленными, называются полностью целочисленными, а задачи, в которых лишь некоторые переменные должны принимать целочисленные значения, — частично-целочисленными.

Пример 6.2-1. (Распределение капиталовложений)

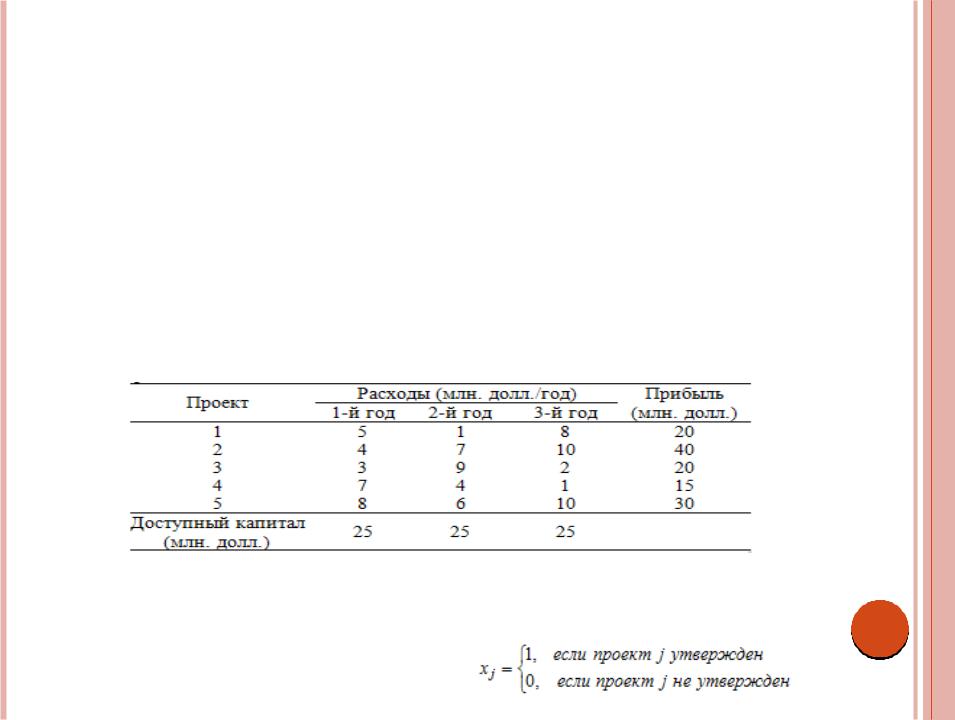
Оценивается пять проектов с точки зрения их возможного финансирования на предстоящий трехлетний период. Следующая таблица содержит ожидаемую прибыль от реализации каждого проекта и распределение необходимых капиталовложений по годам.

Предполагается, что каждый утвержденный проект будет реализован за трехлетний период. Необходимо определить совокупность проектов, которой соответствует максимум суммарной прибыли.

Задача сводится к решению типа "да - нет" относительно каждого проекта. Определим двоичные переменные хj:

Задача ЦЛП будет записана следующим образом. Максимизировать

z = 20х1 + 40х2 + 20х3 + 15х4 + 30х5 при ограничениях

5x1 + 4х2 + 3х3 + 7х4 + 8х5 25, х1 + 7х2 + 9х3 + 4х4 + 6x5 25, 8x1 + 10х2 + 2х3 + x4 + 10x5 25, х1, х2, х3, х4, x5 = 0 или 1.

Оптимальным целочисленным решением является х1 = х2 = х3 = х4 = 1, х5 = 0 с z = 95 (млн. долл.). Это решение означает, что необходимо выбрать для финансирования все проекты, кроме пятого.

Интересно сравнить решение данной задачи ЦЛП с решением "обычной" задачи ЛП с теми же ограничениями, но без условия целочисленности переменных. Задача линейного программирования получается в результате замены условия хj = 0 или 1 на ограничение 0 хj 1 для всех

j. Эта задача имеет решение х1 = 0.5789, х2 = х3 = х4 = 1, х5 = 0.7368 и z =

108.68 (млн. долл.). Такое решение с точки зрения целочисленной задачи лишено смысла, так как две переменные принимают дробное значение. Можно было бы попытаться округлить полученный результат, что привело бы к х1 = х5 = 1. Полученное при этом решение является

недопустимым, так как нарушаются ограничения задачи. Более существенным в этой ситуации является то, что округление применять нельзя, так как хj представляет решение типа "да - нет", для которого

дробные значения лишены смысла.

8.3.МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

Методы решения задач целочисленного линейного программирования основаны на использовании вычислительных возможностей методов линейного программирования. Обычно алгоритмы целочисленного программирования включают три шага.

Шаг 1. "Ослабление" пространства допустимых решений задачи целочисленного линейного программирования путем замены любой двоичной переменной y непрерывным ограничением 0 у 1 и отбрасывания требования целочисленности для всех остальных переменных. В результате получается обычная задача линейного программирования.

Шаг 2. Решение задачи линейного программирования и определение ее оптимального решения.

Шаг 3. Имея полученное (непрерывное) оптимальное решение, добавляем специальные ограничения, которые итерационным путем изменяют пространство допустимых решений задачи линейного программирования таким образом, чтобы, в конечном счете, получилось оптимальное решение, удовлетворяющее требованиям целочисленности.

Разработаны два общих метода генерирования специальных ограничений, о которых идет речь при реализации шага 3.

Метод ветвей и границ.

Метод отсекающих плоскостей.

Хотя ни один из упомянутых методов не дает надежных результатов при решении задачи целочисленного линейного программирования, опыт вычислений свидетельствует, что метод ветвей и границ более успешно решает задачу, чем метод отсекающих плоскостей.

Если мы продолжим разумно исключать из рассмотрения области, не содержащие целочисленных решений (такие, как 3 < х1 < 4), путем введения надлежащих ограничений, то в конечном счете получим задачу линейного программирования, оптимальное решение которой удовлетворяет требованиям целочисленности. Другими словами, будем решать задачу ЦЛП путем решения последовательности непрерывных задач линейного программирования.

Новые ограничения х1 3 и х1 4 взаимоисключаемы, так что задачи ЛП1 и ЛП2 необходимо рассматривать как независимые задачи линейного программирования, что и показано на рис. 6.8. Дихотомизация задач ЛП — основа концепции ветвления в методе ветвей и границ. В этом случае х1 называется

переменной ветвления.

Рис. 6.8

Оптимальное решение задачи ЦЛП находится в пространстве допустимых решений либо задачи ЛП1, либо ЛП2. Следовательно, обе подзадачи должны быть решены. Выбираем сначала задачу ЛП1 (выбор произволен), имеющую

Максимизировать z = 5х1 + 4х2 при ограничениях

х1 + х2 5, 10x1 + 6х2 45, х1 3,

х1, х2 0.

Оптимальным решением задачи ЛП1 (которое можно получить с помощью метода решения задач с ограниченными переменными, изложенного в разделе 7.5.2) является х1 = 3, х2 = 2 и

z = 23.

Оптимальное решение задачи ЛП1 удовлетворяет требованию целочисленности переменных х1 и х2. В этом случае говорят, что задача ЛП1 прозондирована. Это означает,

что задача ЛП1 не должна больше зондироваться, так как она не может содержать лучшего решения задачи ЦЛП.

Мы не можем в этой ситуации оценить качество целочисленного решения, полученного из рассмотрения задачи ЛП1, ибо решение задачи ЛП2 может привести к лучшему целочисленному решению (с большим значением целевой функции z). Пока мы можем лишь сказать, что значение z = 23 является нижней границей оптимального (максимального) значения целевой функции исходной задачи ЦЛП. Это значит, что любая нерассмотренная подзадача, которая не может привести к целочисленному решению с большим значением целевой функции, должна быть исключена из рассмотрения, как бесперспективная. Если же нерассмотренная подзадача может привести к лучшему целочисленному решению, то нижняя граница должна быть надлежащим образом изменена.

При значении нижней границы z = 23 исследуем задачу ЛП2 (единственную оставшуюся нерассмотренную подзадачу). Так как в задаче ЛП0 оптимальное значение целевой функции равно 23.75 и все ее коэффициенты являются целыми числами, то невозможно получить целочисленное решение задачи ЛП2 (пространство решений которой более узко, чем в задаче ЛП0), которое будет лучше имеющегося. В результате мы отбрасываем подзадачу ЛП2 и считаем ее прозондированной.

Реализация метода ветвей и границ завершена, так как обе подзадачи ЛП1 и ЛП2 прозондированы (рассмотрение первой привело к нахождению целочисленного решения, а

Остались без ответа два вопроса, связанные с реализацией описанной вычислительной процедуры.

Можно ли было в задаче ЛП0 выбрать переменную х2 в качестве переменной ветвления вместо х1?

Можно ли было при выборе подзадачи для зондирования решить сначала задачу ЛП2 вместо ЛП1?

Ответы на оба вопроса положительные. Однако последующие вычисления могут значительно отличаться.

Последовательность решения подзадач, показанная на рис. 6.9 (ЛП0, ЛП2, ЛП4, ЛП3, ЛП6, ЛП5, ЛП1), является наихудшей; тем не менее, она встречается на практике. Этот пример указывает на основную слабость метода ветвей и границ: как выбирать следующую подзадачу для исследования и как выбирать для нее переменную ветвления?

В процессе решения, представленного на рис. 6.8, мы случайно наткнулись на хорошую нижнюю границу значений целевой функции на самой первой подзадаче ЛП1, что позволило прозондировать ЛП2 без детальных исследований и закончить вычисления. По существу, мы завершили вычисления, решив лишь одну подзадачу. В процессе решения, представленном на рис. 6.9, мы были вынуждены исследовать семь подзадач, и лишь тогда завершились вычисления метода ветвей и границ. Хотя имеются эвристические соображения, позволяющие "угадать", какая из ветвей может привести к улучшенному решению задачи ЦЛП, не существует строгой теории, которая всегда обеспечивала бы надежные результаты.

Теперь сформулируем алгоритм метода ветвей и границ в общем случае. Предположим, что рассматривается задача максимизации. Зададим нижнюю границу оптимального значения целевой функции z задачи ЦЛП равной - . Положим i = 0.