6. Квадратичные формы

Пусть E – евклидово пространство. Функция двух переменных A, ставящая в соответствие каждой паре векторов число A, называется билинейной формой, если она удовлетворяет следующим условиям:

A(x₁+x₂,y)=A(x₁,y)+A(x₂,y);

A(x,y₁+y₂)=A(x,y₁)+A(x,y₂);

A(x,y)=A(x,y);

A(x, y)=A(x,y).

Билинейная форма A(x,y) называется симметрической, если A(x,y)=A(y,x) для любых x,y.

Пусть A(x,y) – симметрическая билинейная форма в n-мерном евклидовом пространстве . Функция A(x,x) называется квадратичной формой. Если – базис в, то квадратичная форма A(x,x) в этом базисе имеет вид

,

где ;n называется порядком квадратичной формы. Матрица называется матрицей квадратичной формы в базисе. Матрица квадратичной формы является симметрической. Матрица квадратичной формы зависит от выбора базиса. Если в некотором базисе квадратичная форма имеет вид

,

то говорят, что квадратичная форма в этом базисе имеет канонический вид.

Теорема 18. Для любой квадратичной формы существует базис, в котором эта форма имеет канонический вид.

Этой теореме можно придать другую формулировку: любую квадратичную форму можно линейным обратимым преобразованием координат привести к каноническому виду.

Теорема 19. Пусть квадратичная форма задана в и – матрица формы в каноническом базисе. Существует ортонормированный базис в, состоящий из собственных векторов матрицы A, в котором квадратичная матрица имеет канонический вид.

Если U – матрица n-го порядка, столбцы которой составлены из координат собственных векторов матрицы квадратичной формы, образующих ортонормированный базис, то линейное преобразование, приводящее квадратичную форму к каноническому виду, имеет вид

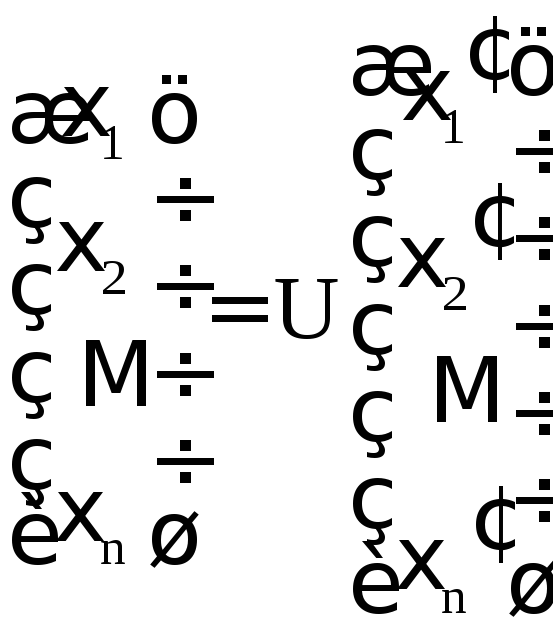. (12)

Такая матрица U называется ортогональной, а преобразование (12) – ортогональным преобразованием.

Пример 11. Найти матрицу А квадратичной формы в каноническом базисе

А(х,х)(13)

Решение. Запишем квадратичную форму в общем виде и сравним коэффициенты при одинаковых степенях

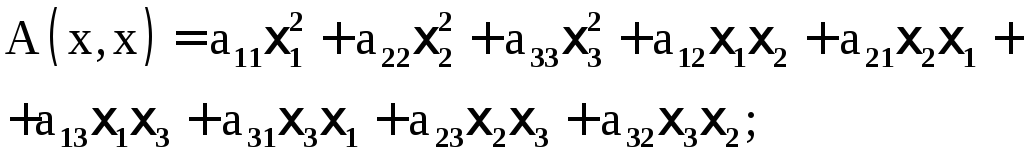
Сравнивая коэффициенты при получимСравним коэффициенты прив обеих формах и учтём, чтотак как матрицаА симметрична. Получим Аналогично

Итак, матрица А квадратичной формы (13) имеет вид:

А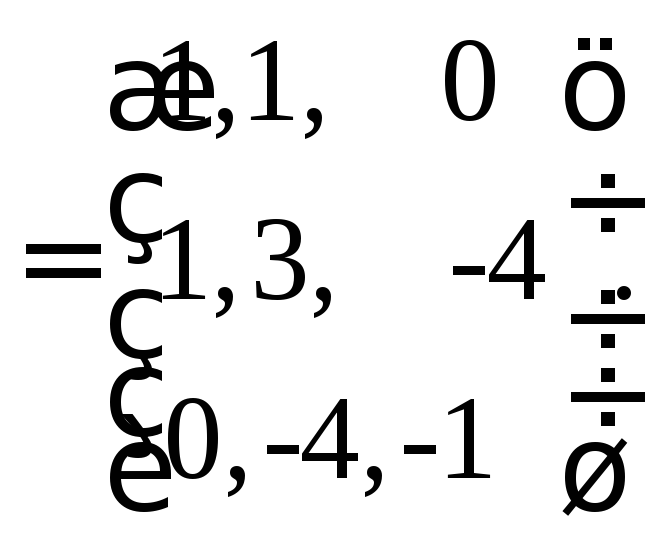

Пример 12. Привести квадратичную форму

в пространстве к каноническому виду ортогональным преобразованием.

Решение. Матрица квадратичной формы имеет вид

.

Найдем собственные значения и собственные векторы матрицы A. Для этого запишем однородное СЛАУ (7)

и решим характеристическое уравнение

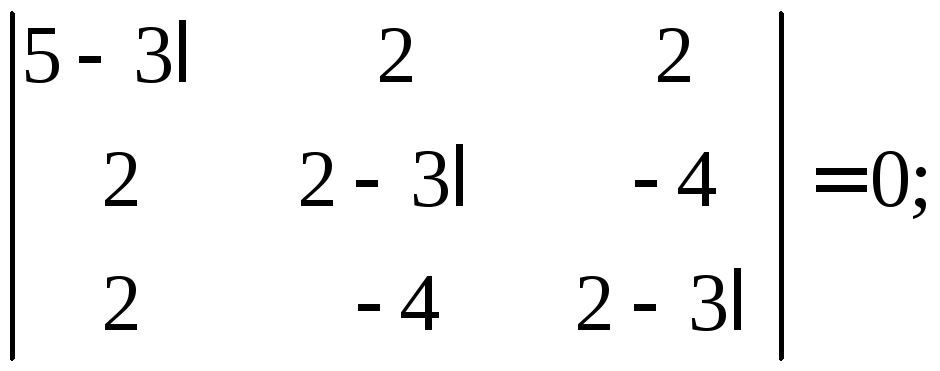
Матрица A имеет два собственных значения: = –1 и =2.

Составим ортонормированный базис, состоящий из собственных векторов матрицы A.

= –1. Получаем систему

Множество решений полученной однородной СЛАУ есть одномерное линейное подпространство в Пусть ₃ = 2. Тогда ₂=2, ₁= –1. Вектор – собственный вектор матрицыA, соответствующий собственному значению = –1. Нормируем его:

, положим .

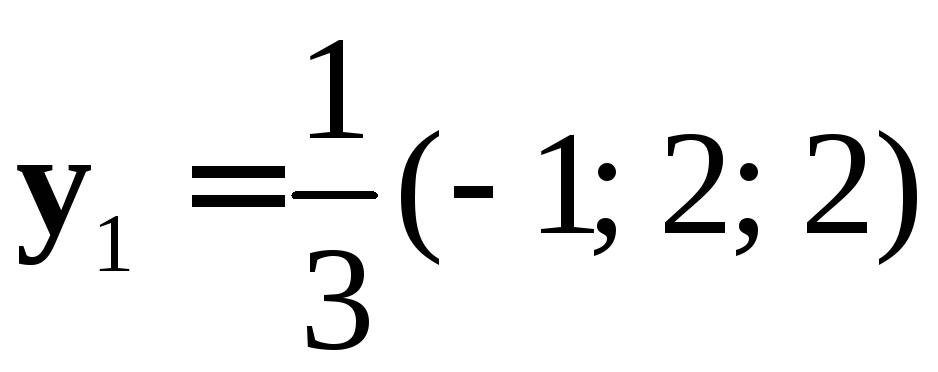=2. Это собственное значение приводит к системе

Эта система равносильна уравнению . Имеем:

Итак, множество решений однородной СЛАУ есть линейное подпространство размерности 2. Следовательно, имеется два линейно-независимых решения, которые образуют фундаментальную систему решений (ФСР) этой СЛАУ. Для нахождения ФСР однородной СЛАУ поступим следующим образом.

Неизвестные ₂ и ₃ объявим свободными. Положим ₂=1 и ₃= 0.Тогда ₁=2 и вектор – собственный вектор, соответствующий собственному значению=2. Нормируя его, получаем другой собственный вектор . Положим₂=0 и ₃=1. Тогда ₁=2 и – другой собственный вектор, соответствующий собственному значению=2.

Пронормируем . Имеем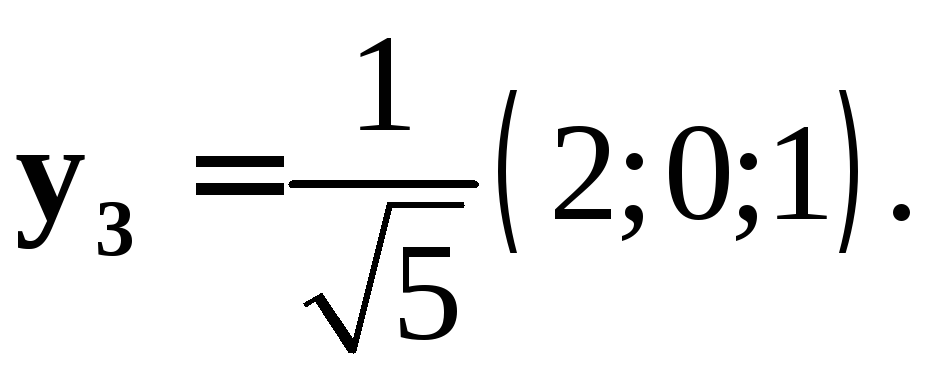

Система векторов у₁, у₂, у₃ образует нормированный базис, но не ортогональный; легко проверяется, что у₁  у₂ , у₁  у₃, но у₂ и у₃ не взаимно ортогональны.

Для ортогонализации базиса положим

.

. Обозначим . Система векторовявляющихся собственными векторами, образует ортонормированный базис, в этом базисе квадратная форма имеет следующий канонический вид:

.

Преобразование, приводящее исходную квадратичную форму к этому каноническому виду, имеет следующий вид:

,

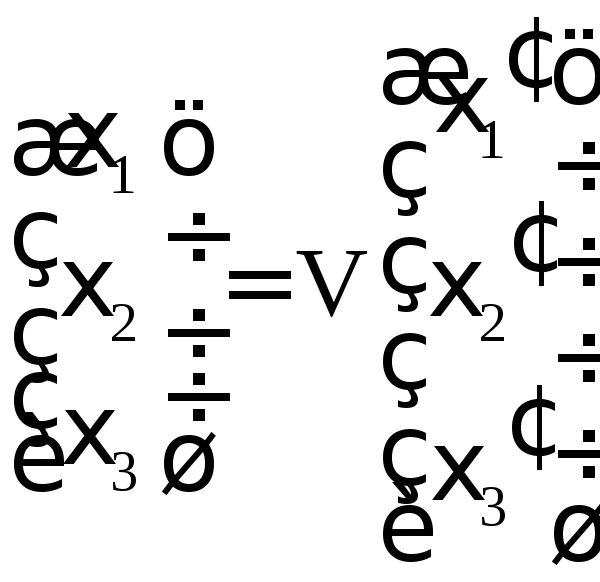где ,

или

Пример 13. A(x,x) = 4x+ 8xx+ 4xx+ 3x– 2x

Привести квадратичную форму к сумме квадратов соответствующих координат методом выделения полных квадратов (методом Лагранжа).

Решение. Будем преобразовывать систему координат так, чтобы в квадратичной форме исчезали произведения координат с различными индексами. Выделим в квадратичной форме слагаемые, содержащие переменную x, и дополним эту сумму до полного квадрата

A(x,x)=+

Дальше, полагая (*)

получим новое выражение для квадратичной формы:

.

В полученной квадратичной форме выделим слагаемые, содержащие , и дополним эту сумму до полного квадрата:

.

Если теперь сделать замену (**)

то квадратичная форма в новой системе координат примет канонический вид:

При этом, подставляя (*) в (**), получим формулы преобразования координат

то есть выражение новых координат через первоначальные координаты.

Одним из применений теории квадратичных форм является приведение уравнений кривых и поверхностей второго порядка к каноническому виду.

Пример 14. Линейным преобразованием координат привести уравнение кривой второго порядка к каноническому виду и определить вид кривой.

Решение. Слагаемые второй степени уравнения образуют квадратичную форму: ; матрица этой формы имеет вид

.

Составим характеристическое уравнение матрицы A:

.

Корни этого уравнения =5 и = –5 являются собственными значениями       матрицы    A.    Найдем         собственные векторы, соответствующие этим собственным значениям. Собственное значение =5 приводит к системе

Эта система, имеющая ранг, равный единице, равносильна уравнению .

Положим ₂=2, тогда ₁=1. Вектор – собственный вектор матрицыA, соответствующий собственному значению =5. Нормируем его и получаем

; .

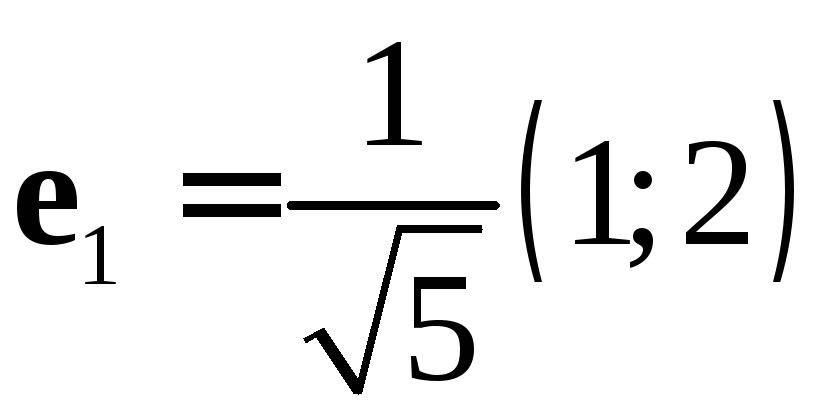Обратившись к собственному значению = –5, получим систему

.

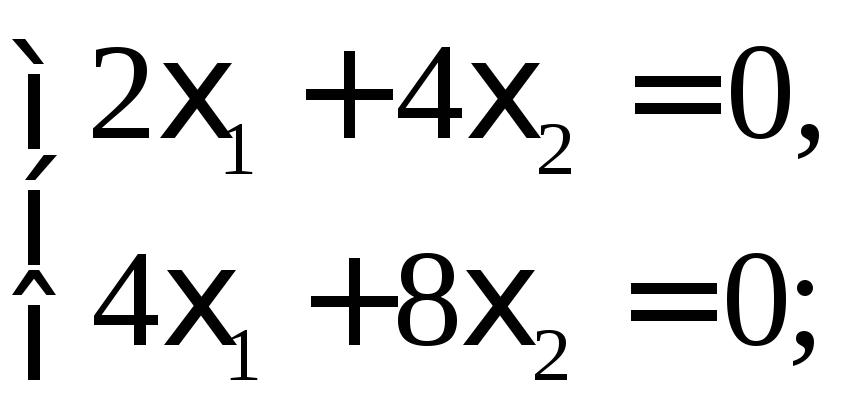
Положим ₂=1, тогда ₁= –2. Пронормировав собственный вектор , получим.

Столбцы координат векторов ортонормированного базиса  образуют матрицуV

.

Запишем ортогональное преобразование, приводящее вышеуказанную квадратичную форму к каноническому виду:

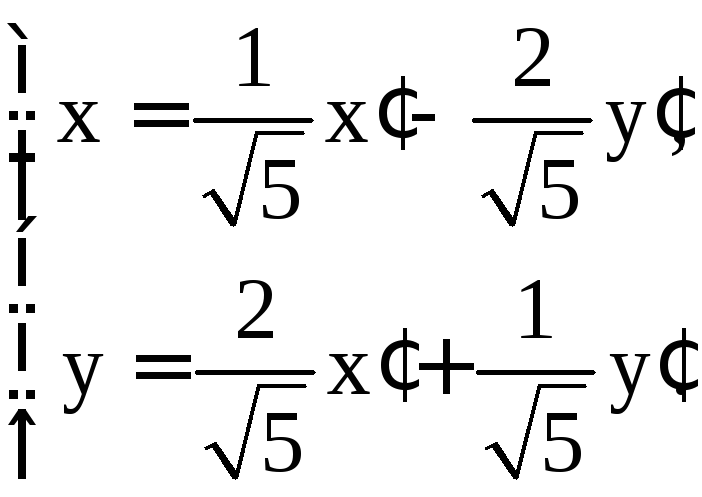
Исходное уравнение при этом преобразовании примет вид

.

Преобразуя это уравнение, получим

,

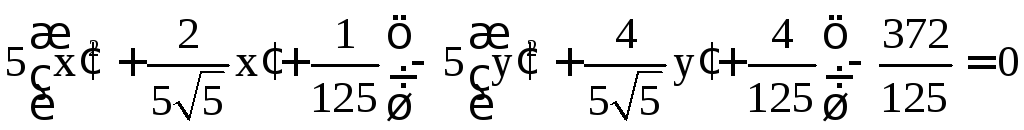или

.

После преобразования параллельного переноса

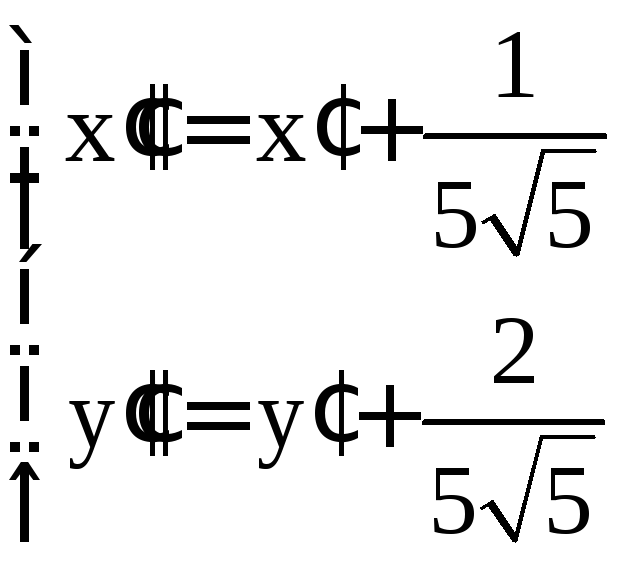
получим уравнение

.

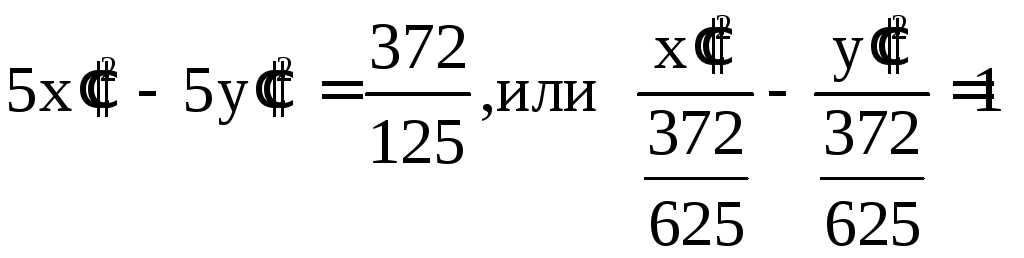Таким образом, исходное уравнение является уравнением гиперболы.