5. Собственные векторы и собственные значения

Пусть A:  линейный оператор. Число  называется собственным значением оператора A, если существует ненулевой вектор x, такой что Ax =x; при этом вектор x называется собственным вектором оператора A, соответствующим собственному значению . В каждом базисе оператору А соответствует своя матрица.

Можно доказать, что собственные векторы и собственные значения оператора будут собственными векторами и собственными значениями соответствующей ему матрицы.

Теорема 13. Множество собственных векторов линейного оператора, отвечающих одному и тому же собственному значению, образует линейное подпространство (конечно же, после присоединения к нему нулевого вектора).

Теорема 14. Пусть линейный оператор A:  в n-мерном линейном пространстве имеет n собственных векторов , образующих линейно независимую систему. Тогда операторA в базисе представлен диагональной матрицей

,

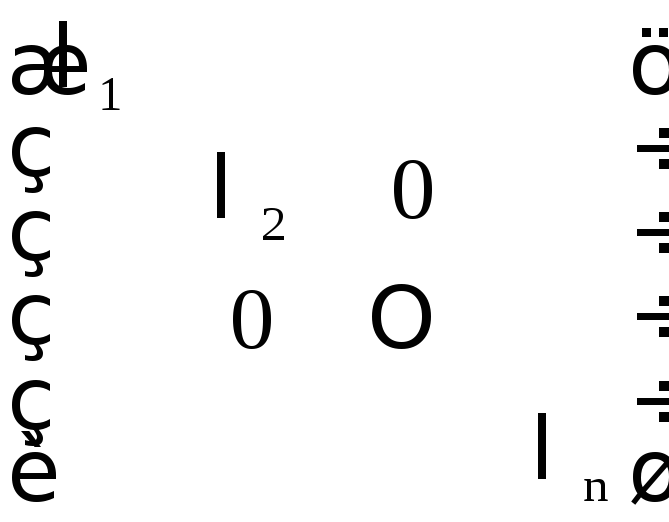где – собственные значения оператора A, отвечающие собственным векторам.

Пусть А– матрица линейного оператораA:  в базисе . Задача нахождения собственных векторов и собственных значений матрицыА сводится к следующей: найти числа , при которых однородная система

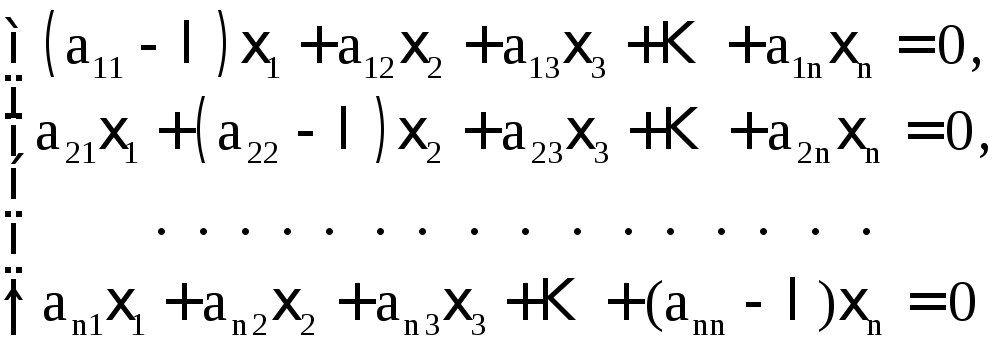(7)

имеет хотя бы одно ненулевое решение. Ненулевое решение 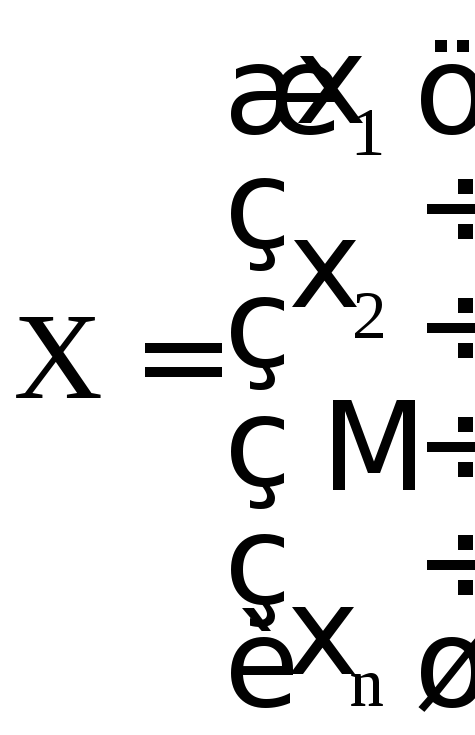этой системы является вектор-столбцом координат собственного вектораx , соответствующего собственному значению .

Известно, что однородная система линейных алгебраических уравнений имеет ненулевое решение в том и только в том случае, когда определитель матрицы системы равен нулю. Поэтому собственные значения линейного оператора (или матрицы) A являются решением алгебраического уравнения n-й степени

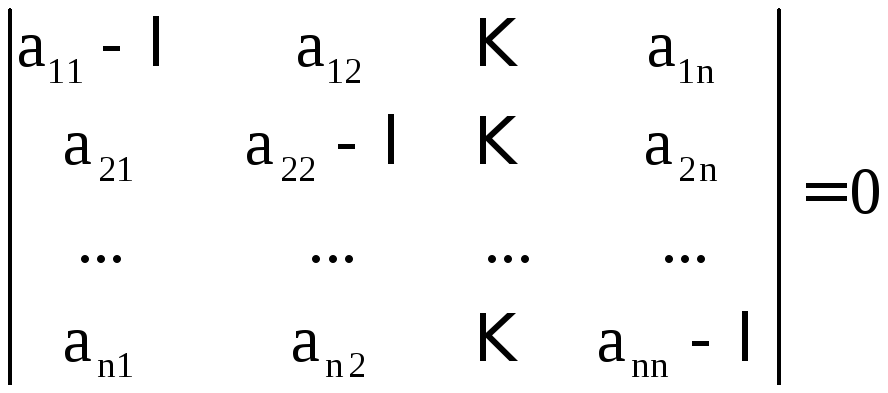, (8)

называемого характеристическим уравнением оператора A. После решения уравнения (8) корни этого уравнения подставляются в систему (7) для нахождения соответствующих собственных векторов.

Пример 9. Найти собственные значения и собственные векторы линейного оператора, заданного в базисе матрицей

1. А; б)А.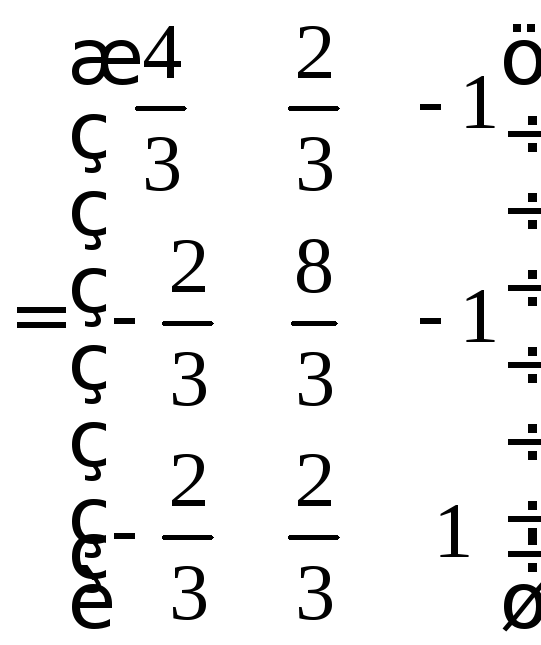

Решение. а) Так как собственные вектора и собственные значения матрицы оператора будут собственными векторами и собственными значениями самого оператора, то для решения задачи найдём собственные вектора и собственные значения матрицы А.

Для нахождения собственных значений и собственных векторов матрицы А запишем однородное СЛАУ (7)

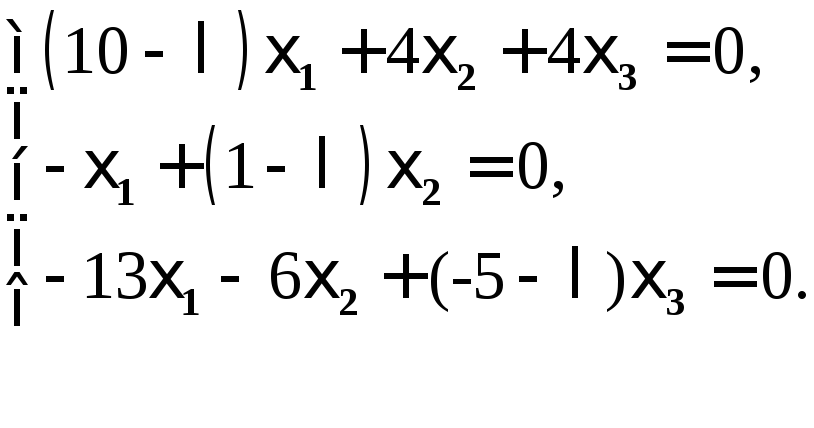(9)

и решим характеристическое уравнение

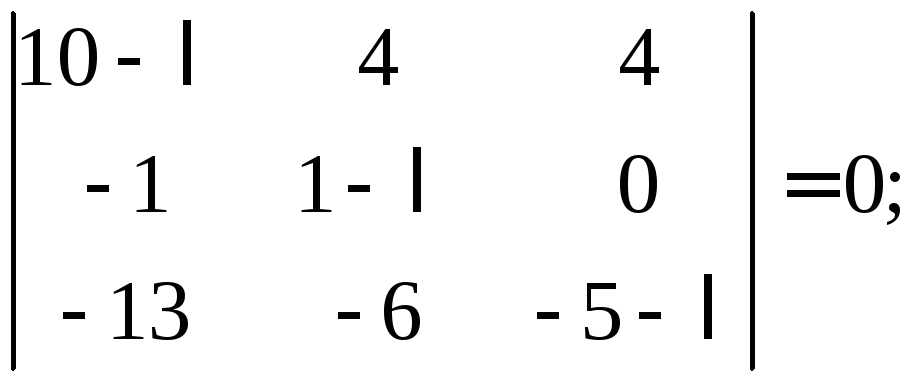
=1, =2, =3 – собственные значения оператора A (матрицы А).

Найдем соответствующие им собственные векторы. Пусть =1.

Подставляя в (9), приходим к системе:

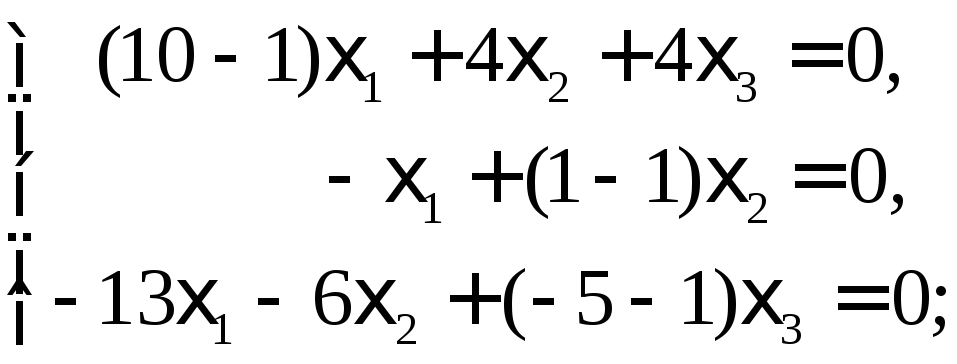
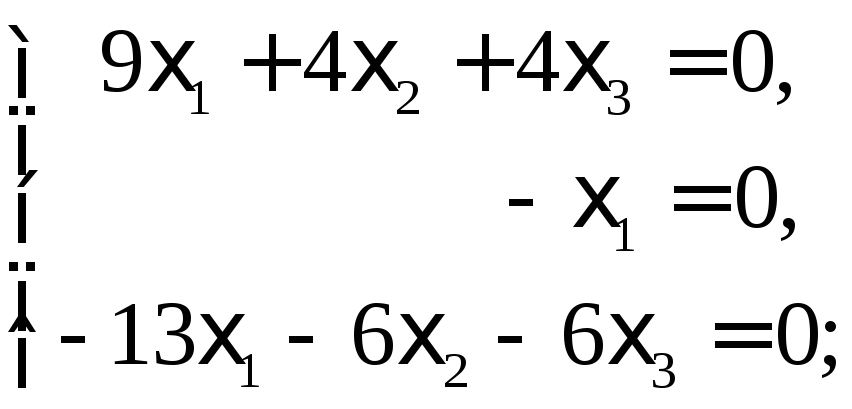или

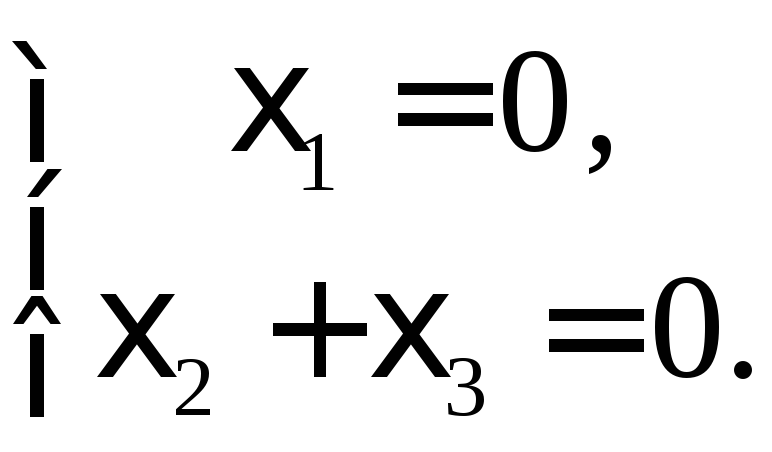(10)

Матрица полученной системы имеет вид: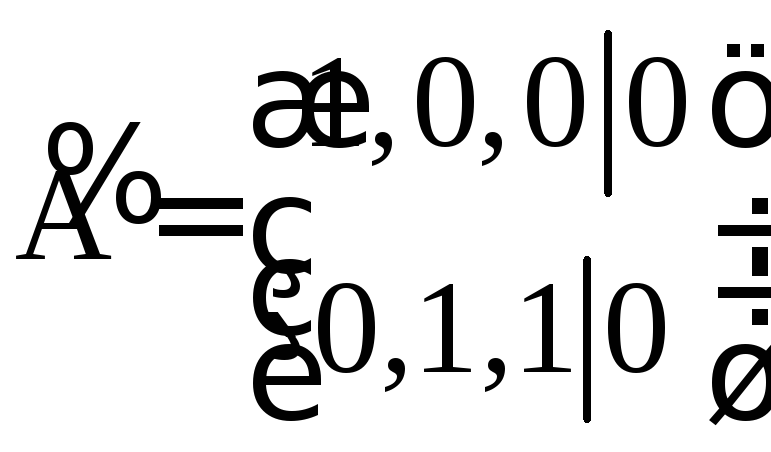. ТогдаИтак, это линейное подпространство размерности 1. Следовательно, имеется одно линейно- независимое решение однородной СЛАУ (10). Положим₃=1. Подставляя это значение в (10), получим Тогда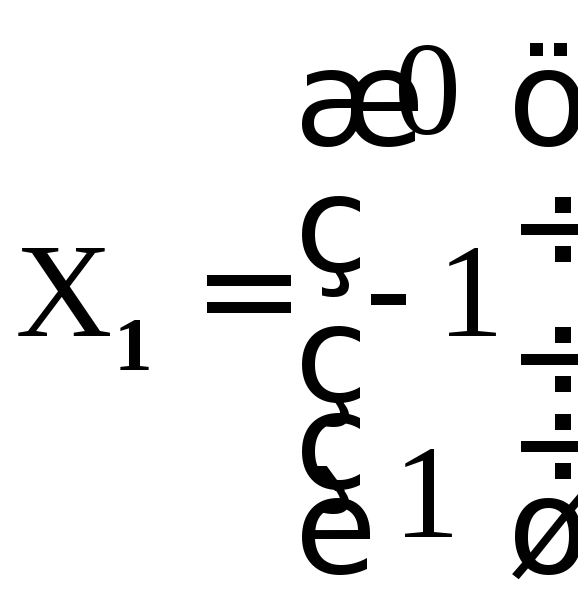– вектор-столбец координат собственного вектора, соответствующего собственному значению=1 (в дальнейшем будем просто говорить, что является собственным вектором оператораA). Множество всех векторов, отвечающих собственному значению =1, имеет вид

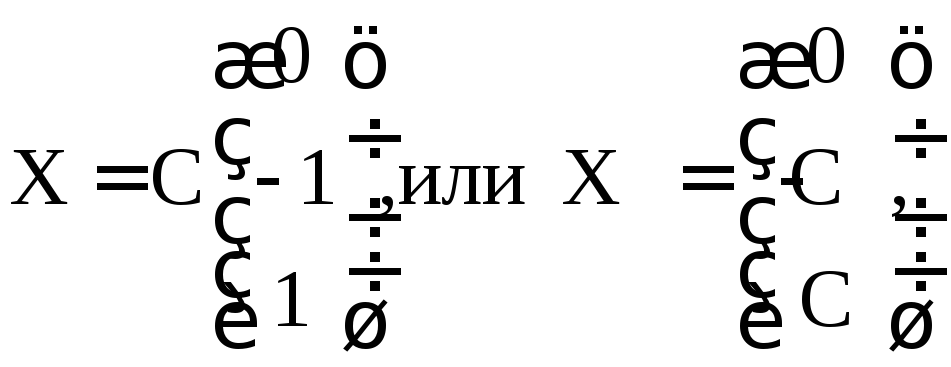
где C – произвольное число, отличное от нуля.

Подставляя в (9), приходим к системе:

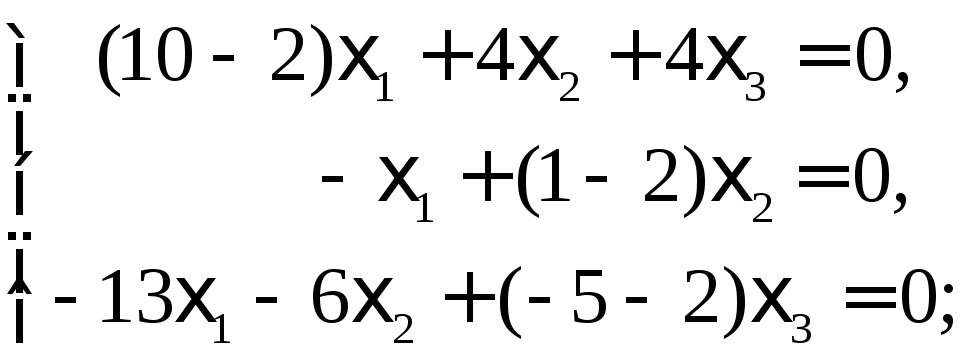
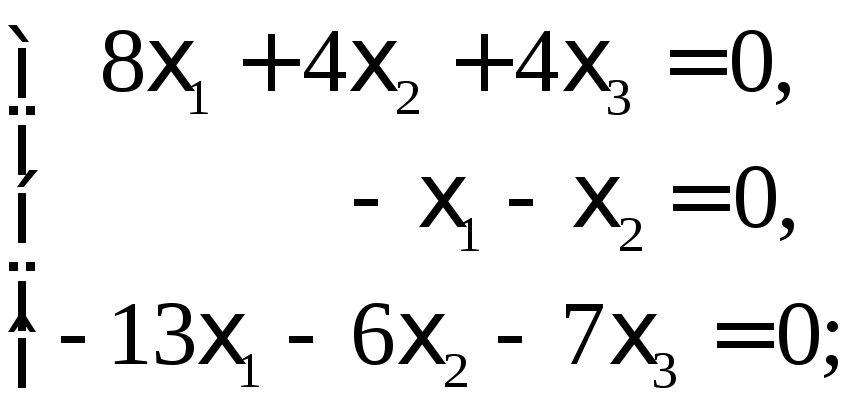
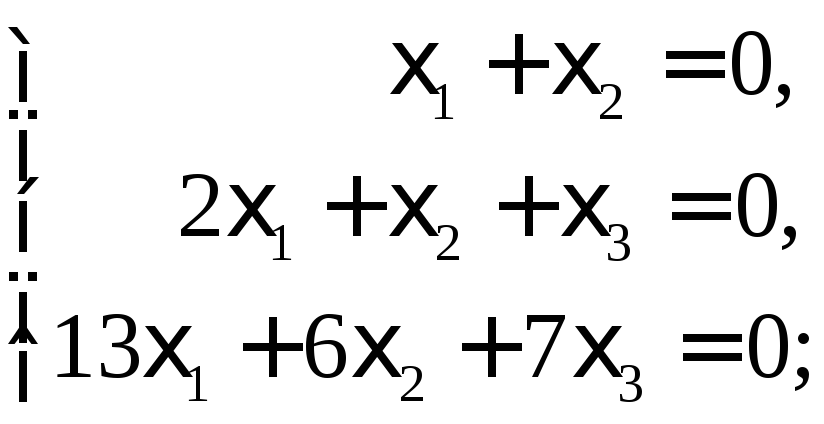
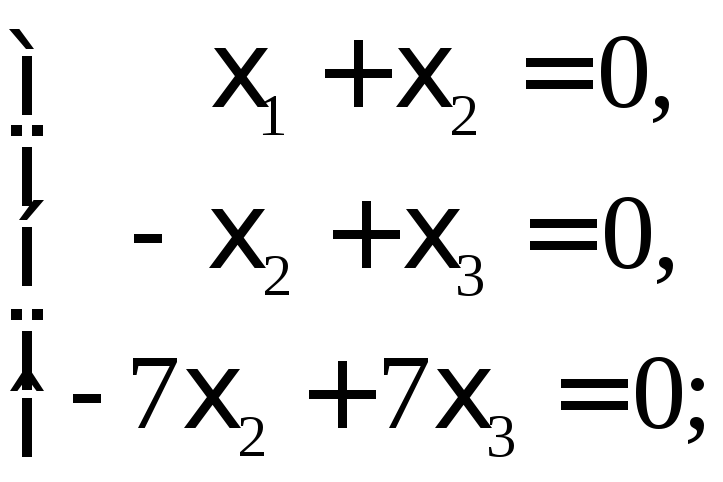
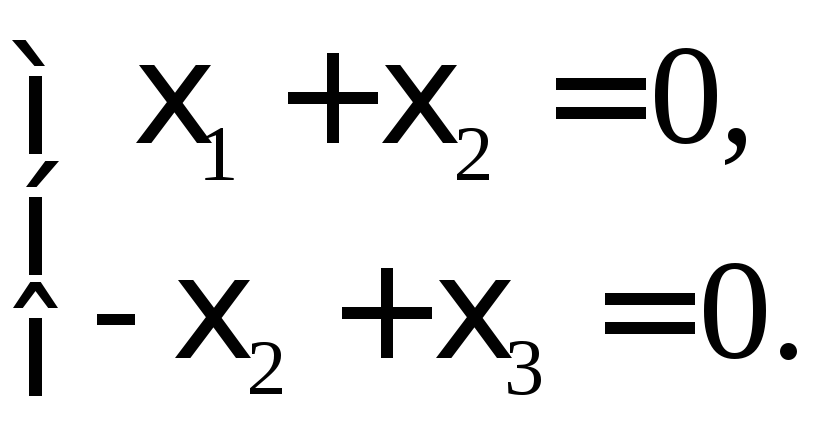(11)

Матрица полученной системы имеет вид: 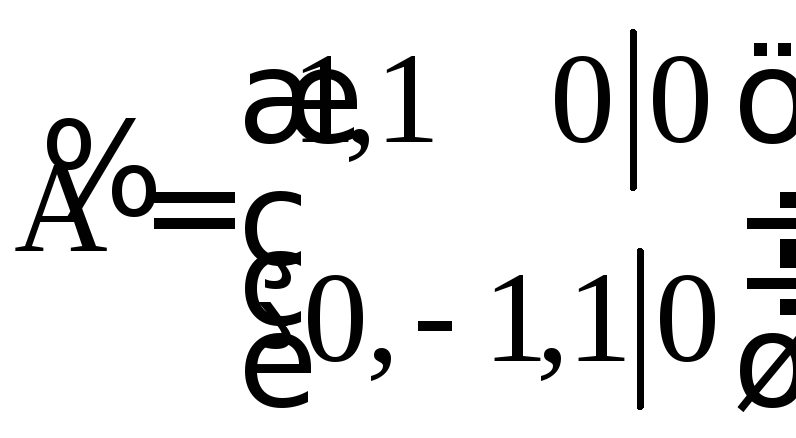. ТогдаИтак, это линейное подпространство размерности 1. Следовательно, имеется одно линейно- независимое решение однородной СЛАУ (11). Объявим₃ свободным неизвестным и положим в (11) ₃=1. Тогда 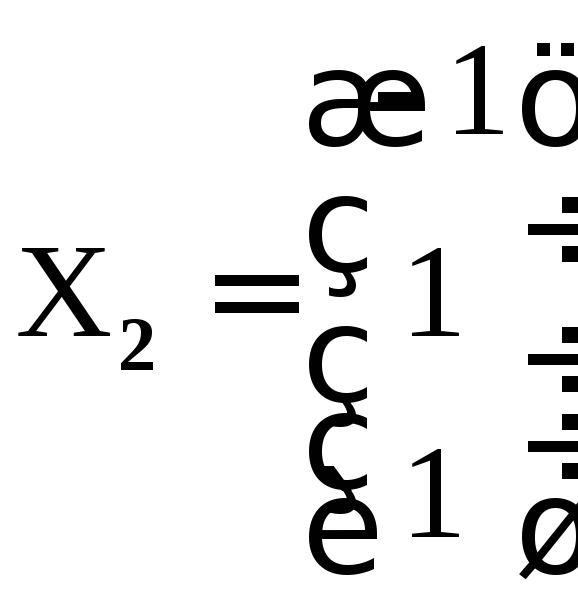– собственный вектор матрицыA. Множество всех векторов, соответствующих собственному значению =2, имеет вид

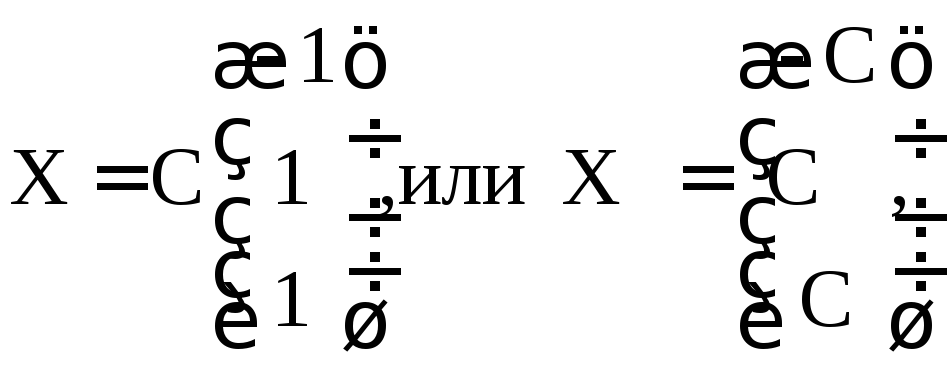
где C – произвольное число, отличное от нуля.

Пусть =3. Получаем систему уравнений:

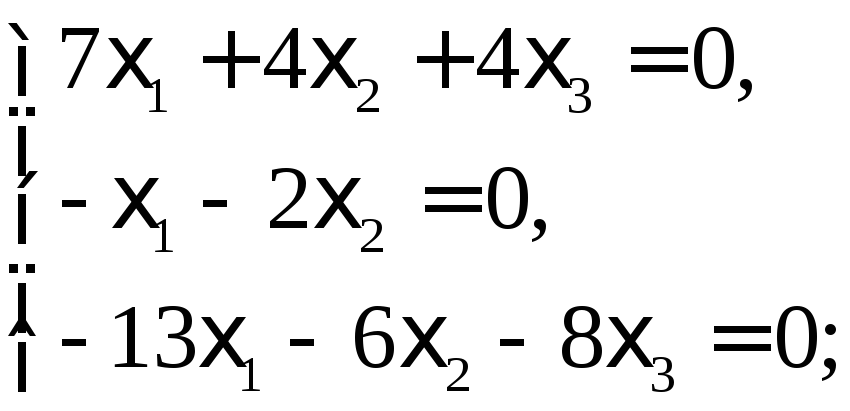
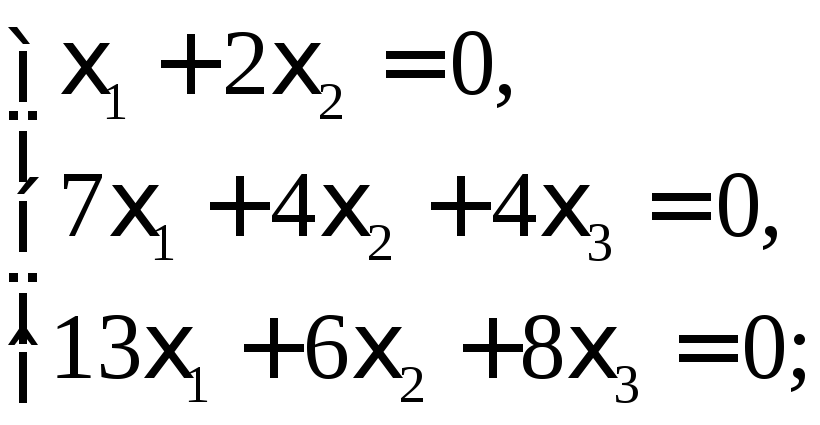
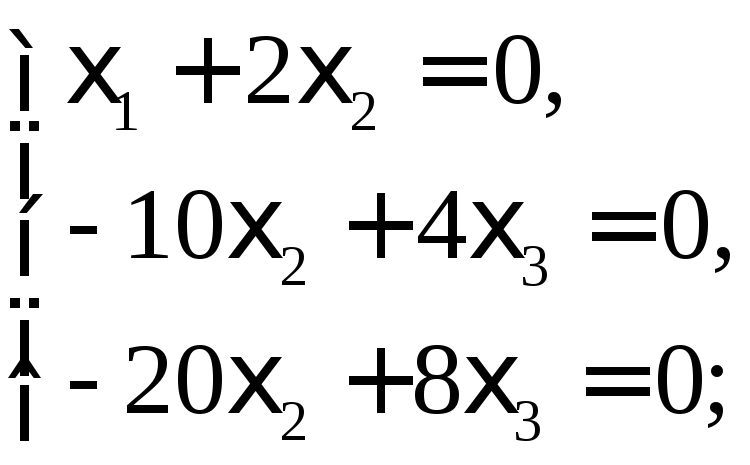
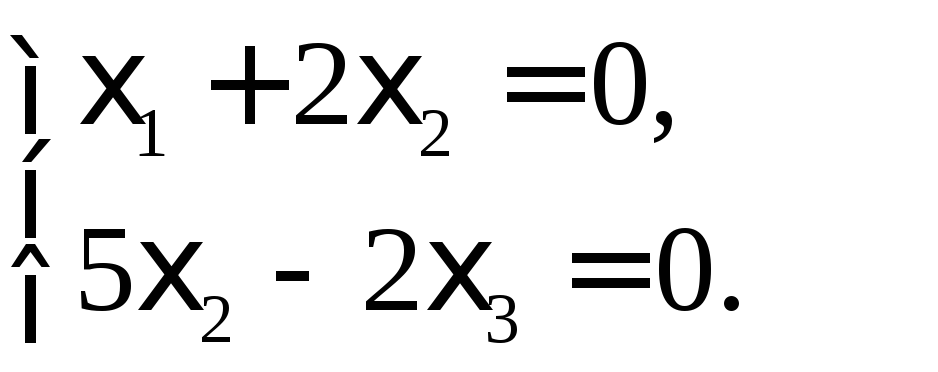
Как и в предыдущих случаях, ранг системы равен 2. Объявим ₃ свободным неизвестным и положим ₃=5. Тогда 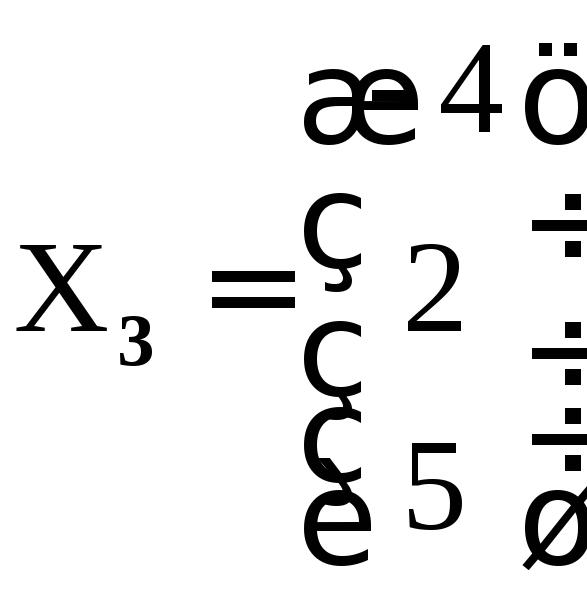– собственный вектор, соответствующий собственному значению=3. Множество всех собственных векторов, отвечающих этому собственному значению, описывается равенством

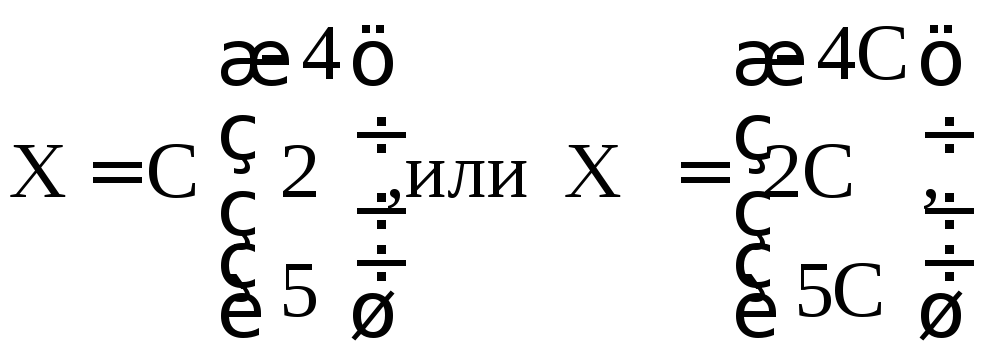
где C0.

б) Для нахождения собственных значений и собственных векторов матрицы А запишем однородное СЛАУ (7)

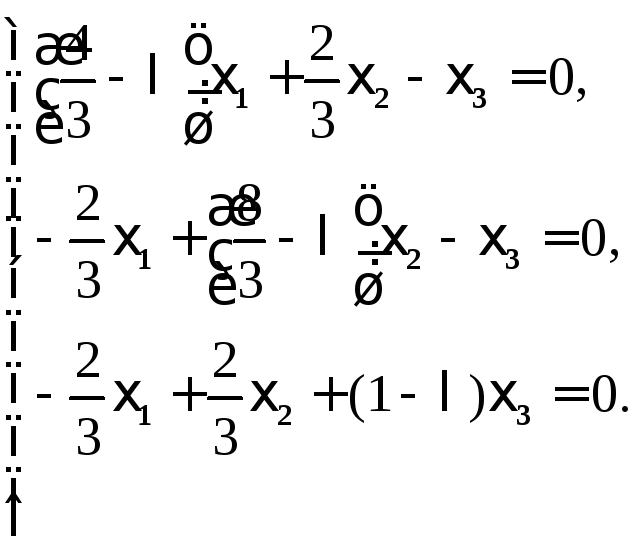
Найдем собственные значения матрицы:

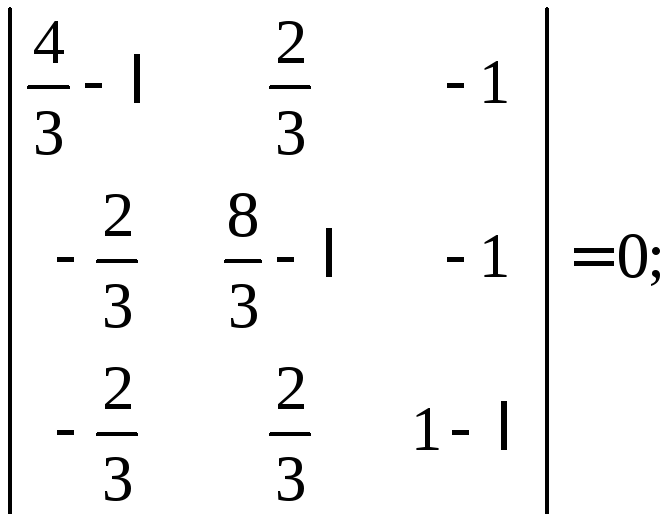
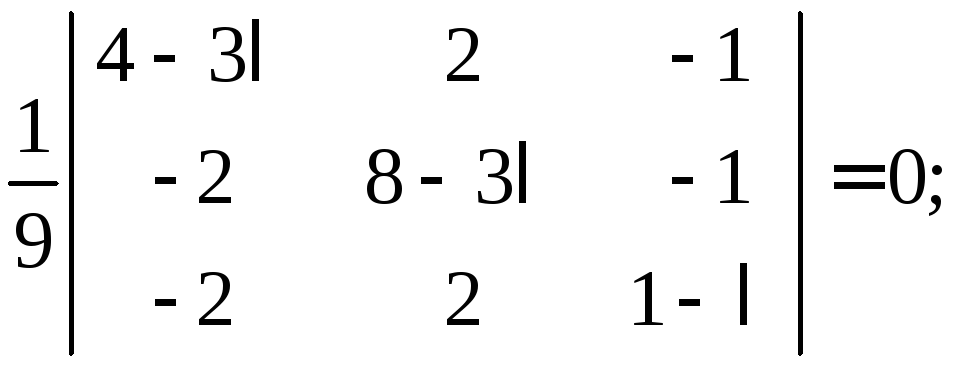
Оператор A имеет два собственных значения: =1 и =2.

Собственному значению =1 отвечает система уравнений

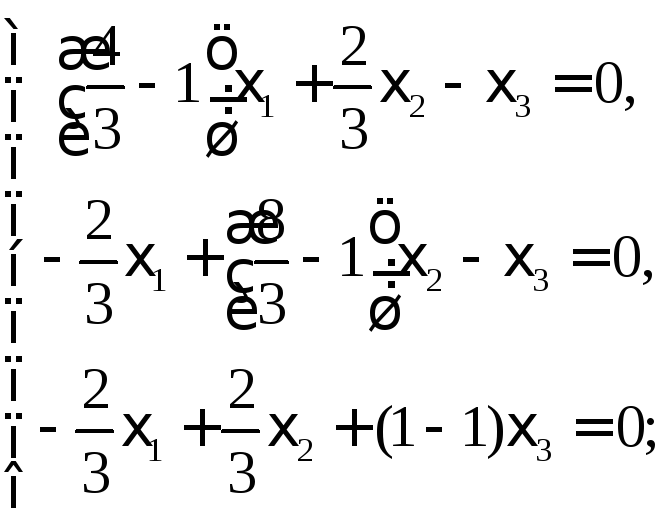
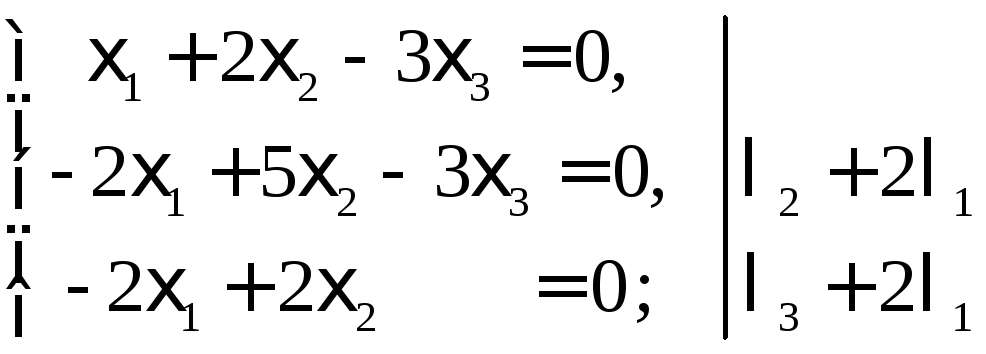
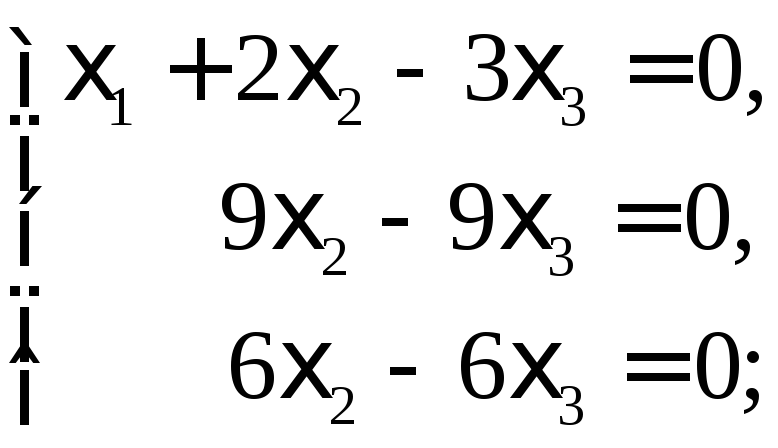
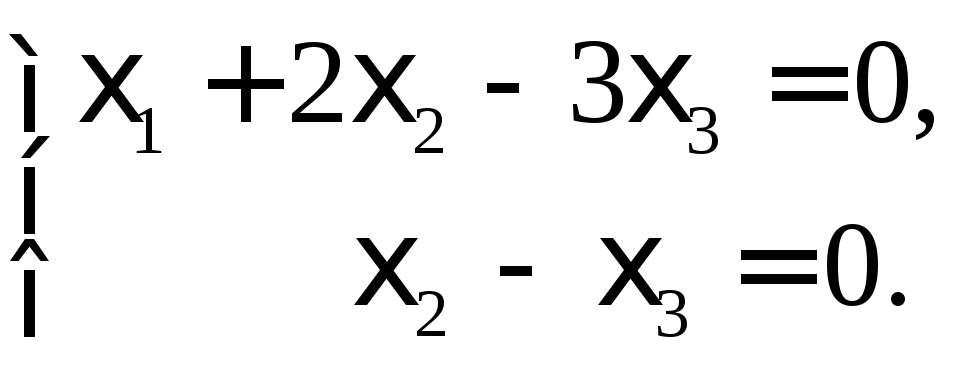
Множество решений полученной однородной СЛАУ есть линейное подпространство размерности 1, так как число неизвестных равняется n=3, а ранг матрицы 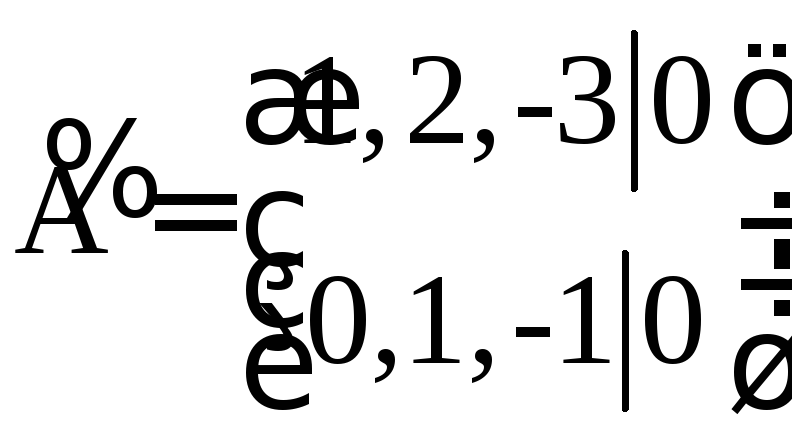равен двум. Следовательно, имеется одно линейно-независимое решение у полученной однородной СЛАУ. Неизвестное₃ объявим свободным и положим ₃=1. Тогда ₂=1 , ₁=1 и 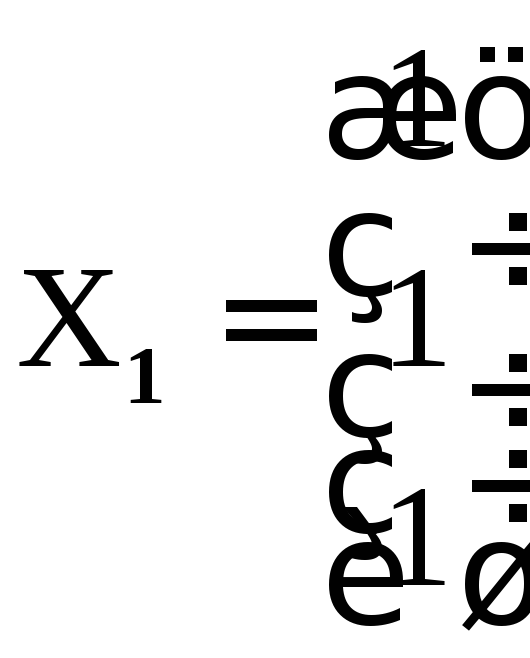– вектор-столбец координат собственного вектора, соответствующего собственному значению=1. Множество всех векторов, отвечающих собственному значению =1, имеет вид

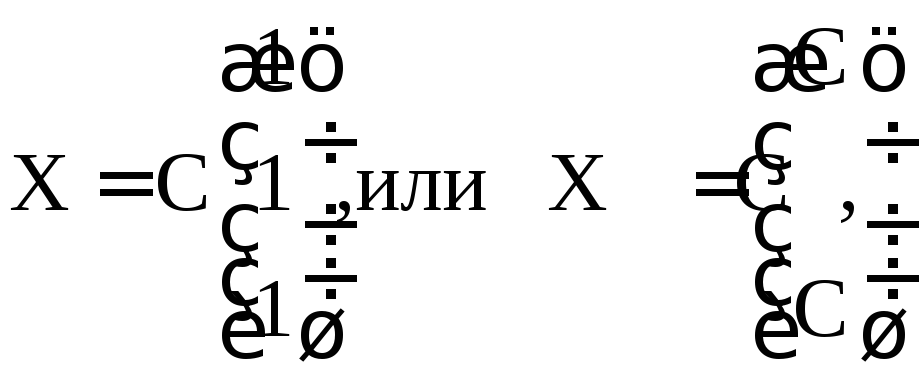
где C – произвольное число, отличное от нуля.

Собственное значение =2 приводит к системе

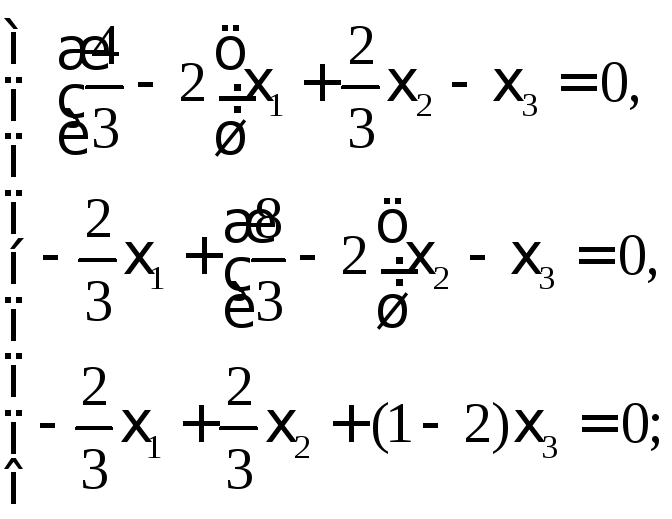
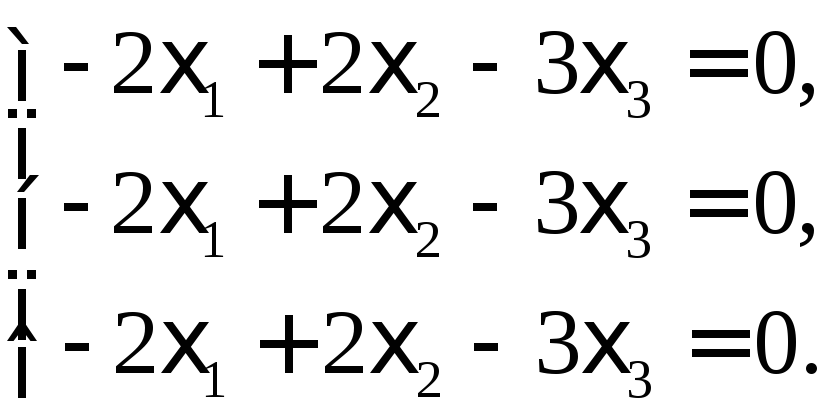
Эта система равносильна уравнению .

Имеем:

Итак, множество решений однородной СЛАУ есть линейное подпространство размерности 2. Следовательно, имеется два линейно-независимых решения, которые образуют фундаментальную систему решений (ФСР) однородной СЛАУ. Для нахождения ФСР однородной СЛАУ поступим следующим образом.

Неизвестные ₂ и ₃ объявим свободными. Положим ₂=1 и ₃= 0, тогда ₁=1. Вектор 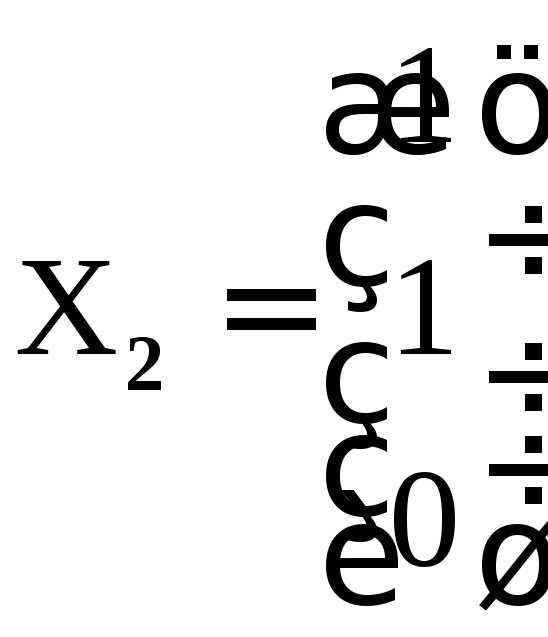является собственным (точнее, вектор-столбцом координат собственного вектора), соответствующим собственному значению=2.

Положим ₂=0 и ₃=1, тогда ₁= –3/2. Вектор 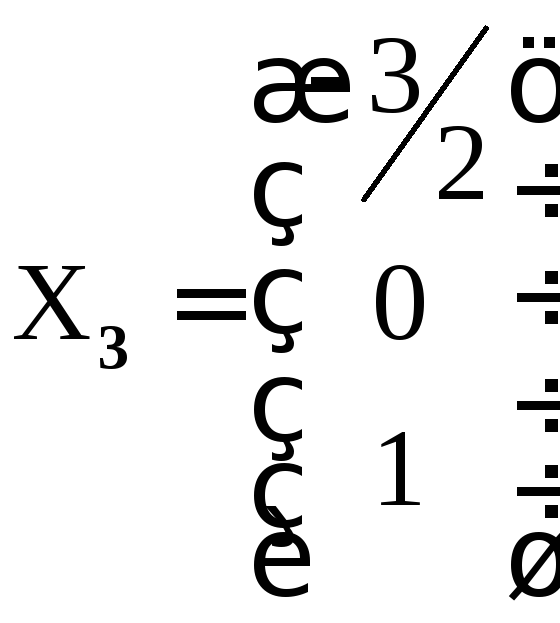– другой собственный вектор, соответствующий собственному значению=2. Векторы илинейно независимы. Множество всех собственных векторов, отвечающих собственному значению=2, имеет вид

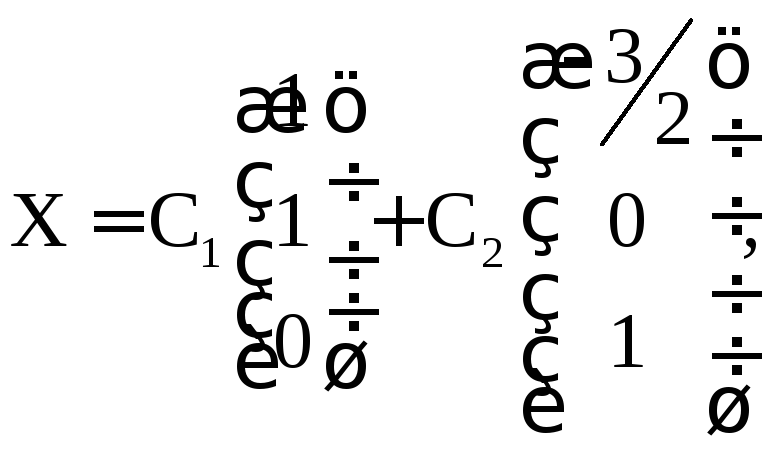
где – произвольные числа, такие что.

Пример 10. Привести матрицу Ак диагональному виду.

Решение. В примере 9 были найдены собственные числа ,,и отвечающие им собственные векторы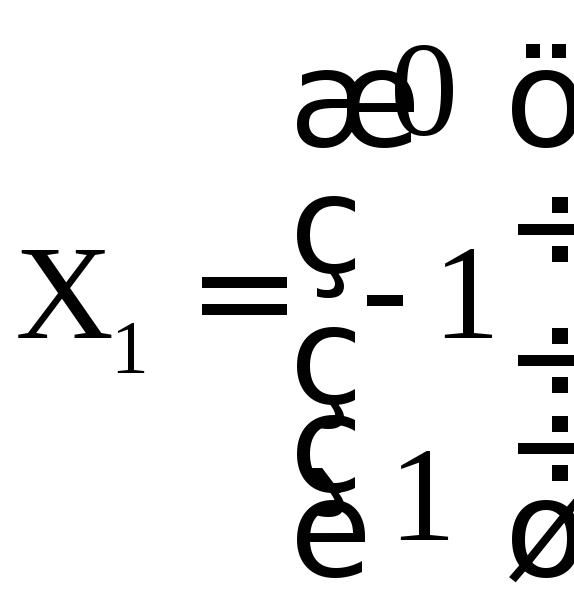,,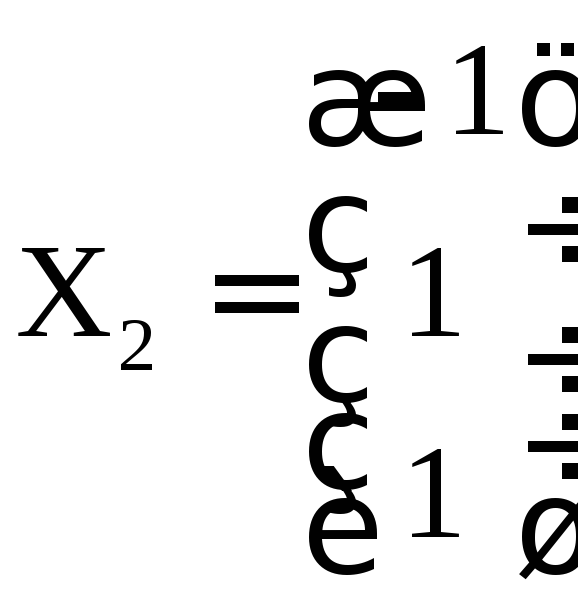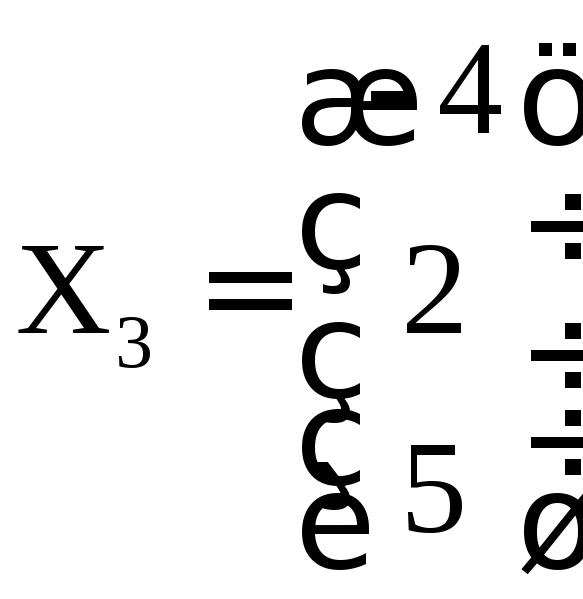матрицы.

Так как собственные векторы матрицы, отвечающие различным собственным значениям, линейно независимы, то векторы ,,образуют базис в.

Воспользуемся теоремой 8. Пусть – линейный оператор, которому в базисеотвечает матрицаA и пусть B – матрица того же оператора в базисе, состоящем из собственных векторов оператора A ,,Тогда матрицаB диагональная и BAC, где С – матрица перехода из базиса в базис.

Столбцы матрицы С есть координаты разложения нового базиса по старому.

Следовательно, .

.

.

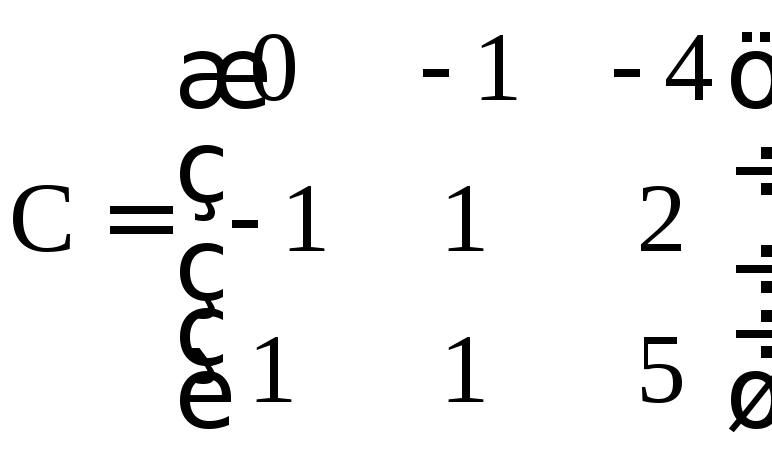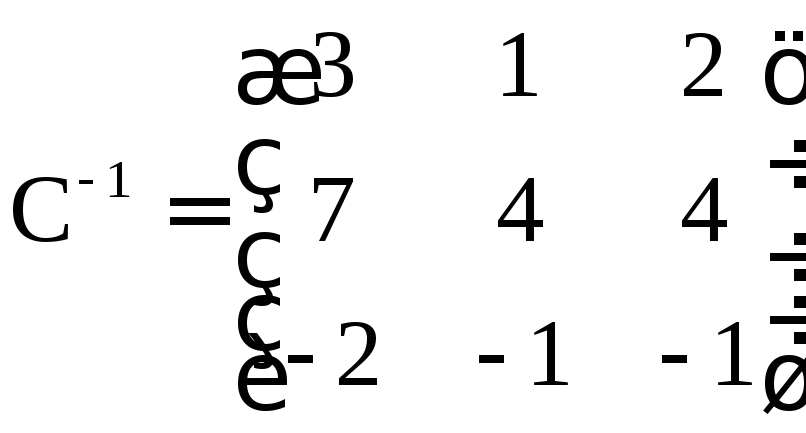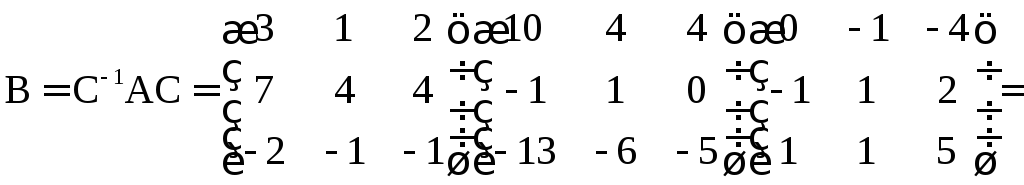
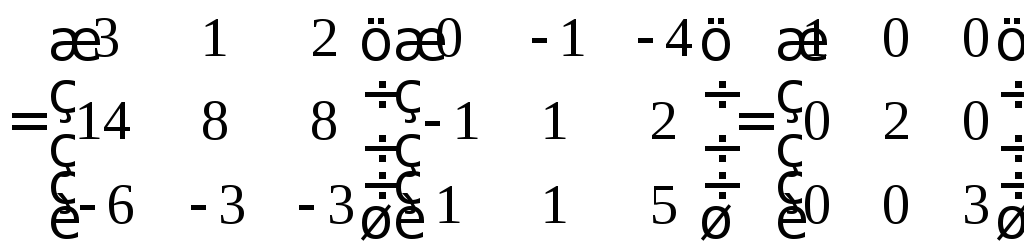Линейный оператор A:в евклидовом пространстве называется самосопряженным, если (A,)=(,A) для любых ,.

Теорема 15. Если – ортонормированный базис в евклидовом пространствеE и A:– самосопряженный оператор, то матрицаоператора A в базисеявляется симметричной:.

Теорема 16. Все собственные значения самосопряженного оператора являются вещественными числами.

Теорема 17. Если A:– самосопряженный оператор в евклидовом пространстве, то существует ортонормированный базис вE, состоящий из собственных векторов оператора A.