X. Элементы линейной алгебры

1. Арифметическое пространство

Рассмотрим множество всевозможных упорядоченных наборов из n чисел (действительных или комплексных) . На этом множестве введем понятие равенства двух элементов и две линейные операции: сложение и умножение на число. Скажем, что элементравен элементутогда и только тогда, когда

Сложение определим по правилу: если ,, то.

Умножение на число определим по правилу: если и – число (действительное или комплексное), то .

Множество всевозможных упорядоченных наборов с введенными выше операциями сложения и умножения на число называется n-мерным арифметическим пространством; будем обозначать его. Элементыпространстваназываются векторами. Векторназывается нулевым вектором.

Выражение называется линейной комбинацией векторов.

Система векторов называется линейно-зависимой, если найдутся числа, не все равные нулю и такие, что

. (1)

Если же равенство (1) возможно лишь при , то системаназывается линейно независимой.

Упорядоченная система, состоящая из n линейно независимых векторов пространства , называется базисом в.

Теорема 1. Система векторов ,…,образует базис вв том и только в том случае, если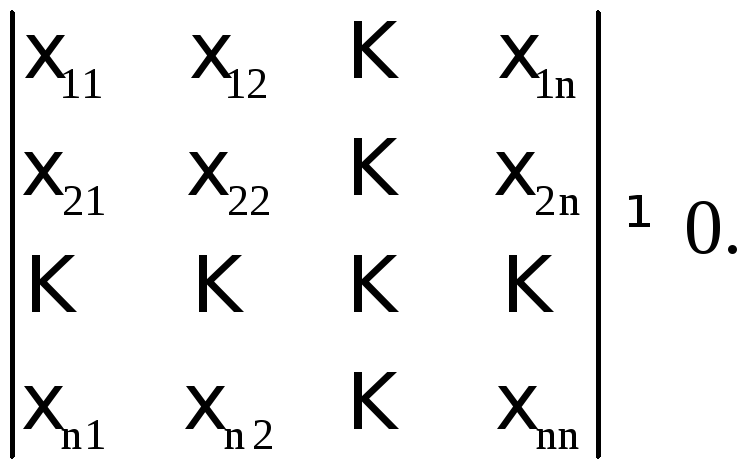

Система векторов ,, …образует базис в, который называется каноническим базисом.

Теорема 2. Пусть задана система векторов

,…,, иА – матрица, составленная из координат этих векторов

А .

Тогда вектора ,,…,линейно независимы вв том и только в том случае, если(Определение и свойства ранга матрицы см. гл.3, п.4).

Если – базис в, то любой векторможет быть представлен в виде линейной комбинации векторов:

(2)

причем такое представление определяется однозначно.

Равенство (2) называется разложением вектора x по базису .

Коэффициенты называются координатами вектораx в базисе .

Пример 1. Убедиться, что система векторов ,

, ,образует базис в . Найти разложение вектора в этом базисе.

Решение. Проверим, что образует базис:

следовательно, образуют базис в .

Найдем разложение вектора в этом базисе, то есть найдем такие, что

Это равенство приводит к системе уравнений

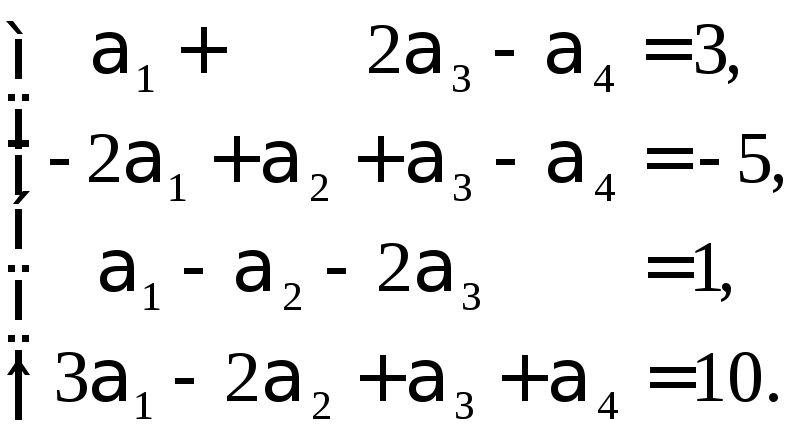
Решением этой системы является .

Таким образом, .

2. Линейное пространство

Пусть – некоторое множество, на котором введены две операции: сложение и умножение на число. Скажем, что множество замкнуто относительно операции сложения и умножения на число, если для любых ии любого вещественного (комплексного) числаПредположим, что операции сложения и умножения на число удовлетворяют следующим условиям:

1) ;

2) ;

3) существует элемент , такой, что для любого элемента (элемент называется нулевым);

4) для любого элемента существует элемент , такой что; при этом пишут, и (–) называется противоположным элементу x;

5) ;

6) ;

7) ;

8)

Множество называется линейным пространством, если в этом множестве введены понятия равенства двух элементов и операции сложения и умножения элемента на число. При этом предполагается, что множество замкнуто относительно операций сложения и умножения на число и для любых элементов из и для любого числа выполняются условия 1 – 8.

Если числа , о которых идет речь в определении линейного пространства, вещественные, то называют вещественным линейным пространством. Если комплексные числа, то называют комплексным линейным пространством. Элементы линейного пространства называются векторами.

Примером линейного пространства является . Другими примерами являются:;– множество всех многочленов степени не вышеn; – множество всех непрерывных нафункций с естественными операциями сложения и умножения на число.

Определение линейной зависимости и независимости системы векторов повторяет соответствующее определение для пространства . Максимальное число линейно независимых векторов пространстваV называется размерностью пространства и обозначается dimV. Например, dim=3 (векторы образуют максимальную линейно независимую систему),dim=n, dim= n+1 (здесь система многочленов образует максимальную линейно независимую систему векторов).

Пусть dimV = n. Упорядоченная система изn линейно независимых векторов пространства называется базисом в . Для линейных n- мерных пространств справедливо равенство (2).

Пусть и– линейные пространства и пусть задано взаимно- однозначное соответствие между пространствамии. Это соответствие называется изоморфизмом, если оно сохраняет линейную структуру пространств, то есть удовлетворяет следующим двум требованиям:

если то;

если и – произвольное число, то.

Пространства, между которыми можно установить изоморфизм, называются изоморфными.

Теорема 3. Конечномерные линейные пространства иизоморфны в том и только в том случае, если.

Пусть – n-мерное линейное пространство и – базис в. Изоморфизм между и можно установить по следующему правилу (элементыбудем записывать в виде столбца, а не строки):

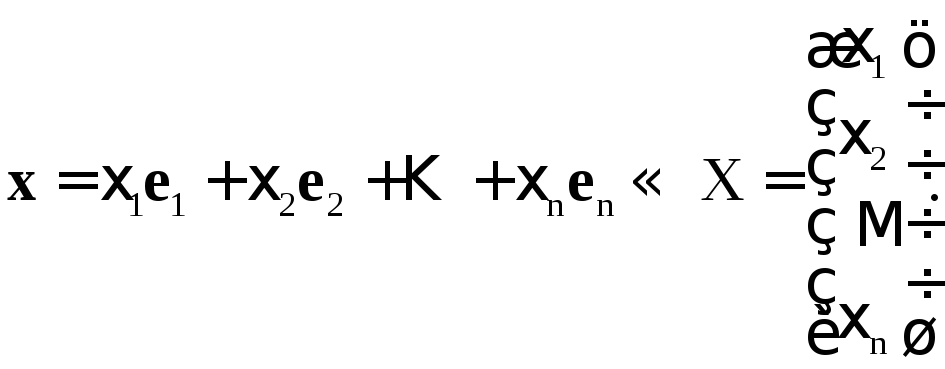
При этом X называется вектор-столбцом координат вектора x.

Теорема 4. Пусть – базис линейного пространства, – система векторовV и

(3)

Система векторов образует базис в том и только в том случае, если матрицаявляется невырожденной. При этом матрицаС, называется матрицей перехода от базиса к базису. Заметим, что по построению матрицы С, её столбцыравны координатам векторов базиса в базисе.

Теорема 5. Пусть базисы ,пространства связаны равенствами (3), иX – вектор-столбец координат вектора x в базисе ,– вектор-столбец координат в базисе . Тогда справедливо равенство

(4)

Пример 2. Пусть – базис линейного пространства и

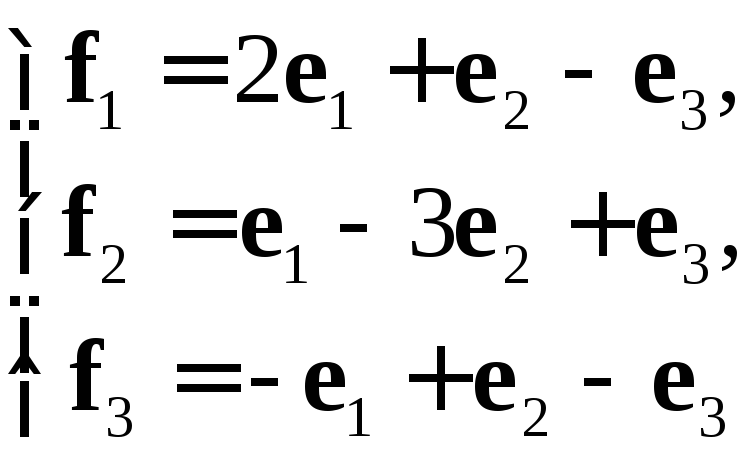
а) доказать, что образуют базис в;

б) найти разложение вектора в базисе.

Решение. а) Построим матрицу перехода от базиса к векторам. Для этого координаты векторав базисе

=(2,1,-1) поставим в первый столбец матрицы С, координаты вектора в базисепоставим во второй столбец матрицы С, координаты векторав базисепоставим в третий столбец матрицы С. То есть

Вычислим определитель матрицы перехода С.

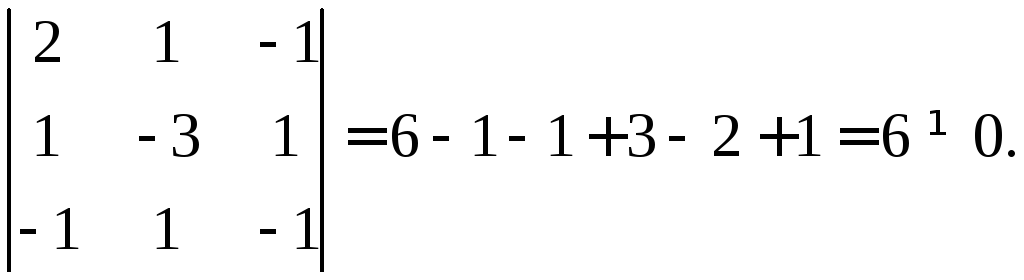
Так как определитель отличен от нуля, то образуют базис.

б) Найдем обратную матрицу:

.

Имеем

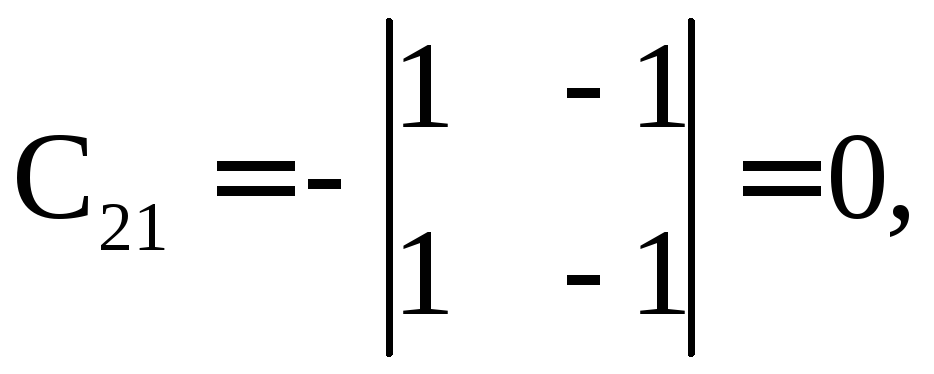
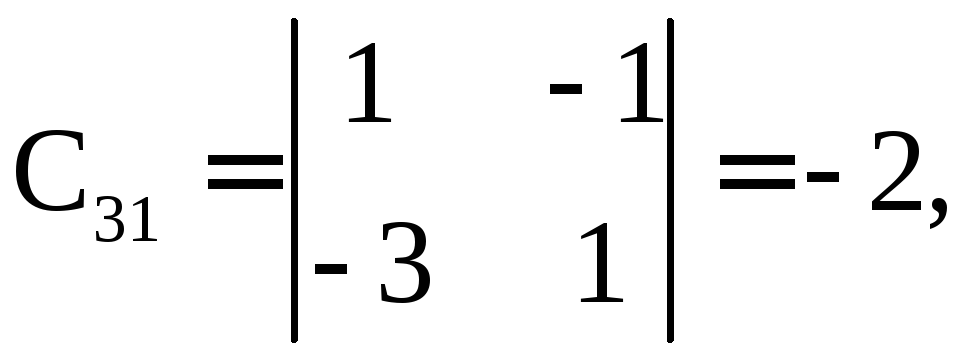
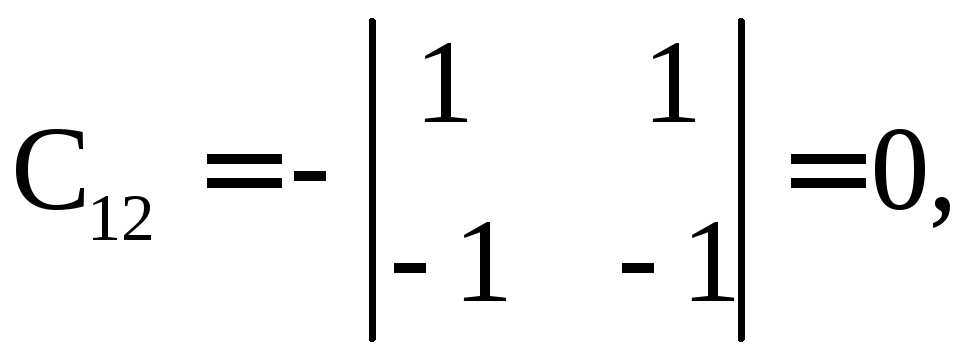
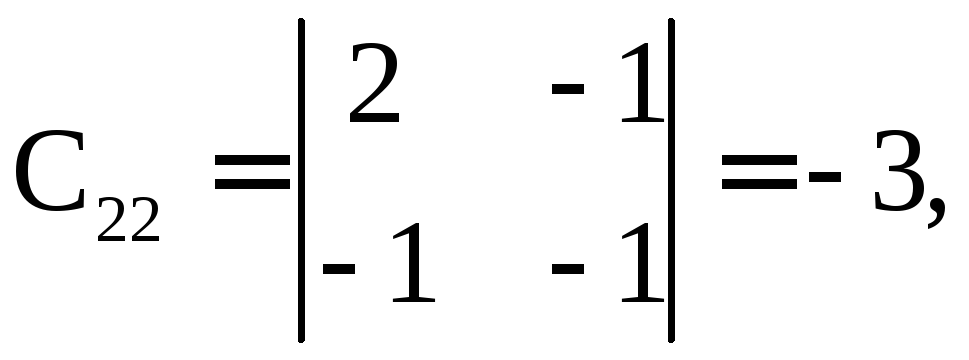
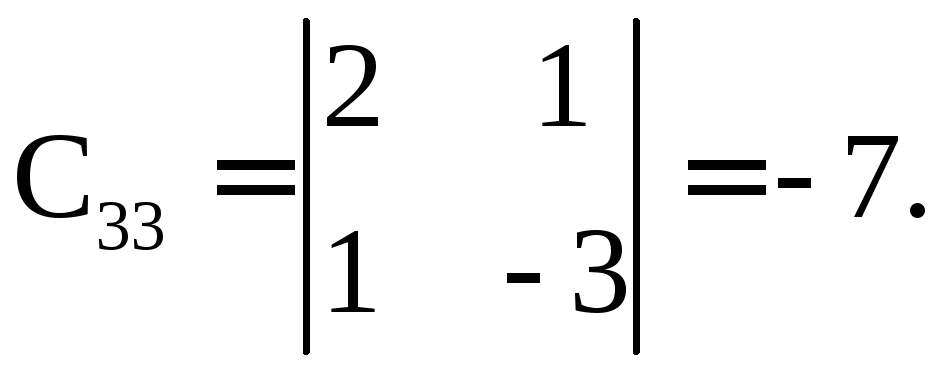
Таким образом,

.

–вектор-столбец координат x в базисе.

Вектор-столбец вектораx в базисе найдем по формуле

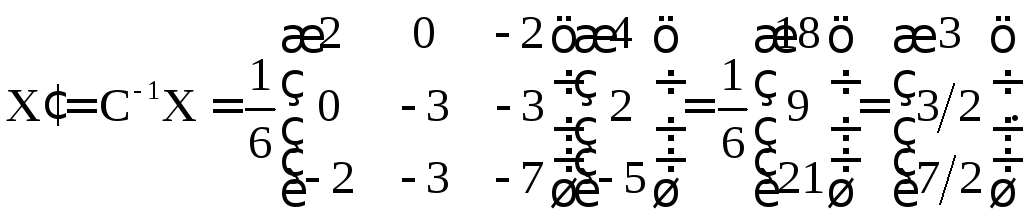
Итак,

Пусть – линейное пространство. Подмножество называется подпространством пространства, еслив свою очередь является линейным пространством.

Пример 3. Образует ли линейное подпространство пространства множество, заданное по правилу:

а)

б) ?

Решение. а) Пусть ,, тогда

Обозначим .

Имеем Следовательно,.

Для произвольного числа  имеем

Это говорит о том, что Из сказанного следует, что является подпространством пространства .

б) Пусть, тогдаРассмотрим вектор.

Имеем

Следовательно, не образует линейного пространства и поэтому не является подпространством пространства .