LabTAU7-9

2.Собрать в MatLab Simulink систему управления с дискретным ПИД–регулятором. Структурная схема в MatLab Simulink совпадает со схемой, используемой в лабораторной работе №5, за исключением применения вместо аналоговых – дискретных передаточной функции

иконтроллера (Discrete Transfer Fcn, Discrete PID-controller).

3.С помощью пакета NCD Blockset выполнить оптимизацию параметров дискретного ПИД-регулятора.

Отчет по лабораторной работе должен содержать:

– краткие теоретические сведения;

– расчет параметров регулятора;

– структурную схему исследованного регулятора;

– графики переходных процессов;

– выводы.

Варианты заданий

Исследуемая передаточная функция системы:

Контрольные вопросы

1.Каков порядок синтеза цифровых систем?

2.Как выполняется дискретная аппроксимация непрерывной части исследуемой системы?

21

3.Для чего используется формирующее звено?

4.Как выбирается тип регулятора?

5.Как проверить устойчивость синтезированной системы?

9. Исследование дискретного модального

регулятора

Цель работы: исследование дискретного модального регулятора средствами Matlab (пакет Simulink).

9.1. Методические указания

Анализ и синтез линейных систем обычно осуществляется одним из двух основных методов. Первый метод основан на использовании преобразования Лапласа и z-преобразования, передаточных функций, структурных схем и графов. Название второго метода – пространства состояний – отождествляют с современной теорией управления, поскольку подавляющее большинство современных методов проектирования систем управления основано на описании и моделировании систем в пространстве состояний.

Вшироком смысле метод пространства состояний, по крайней мере, при изучении цифровых систем управления имеет следующие преимущества перед традиционным частотным методом:

– описание в пространстве состояний является естественным и удобным для решения задач на ЭВМ;

– позволяет унифицировать описание цифровых систем с различными типами квантования;

– позволяет унифицировать описание одномерных и многомерных систем;

– может применяться к некоторым типам нелинейных и нестационарных систем.

Впространстве состояний непрерывная система описывается системой дифференциальных уравнений первого порядка, называемых уравнениями состояния. Для цифровых систем, содержащих только дискретные элементы, уравнения состояния – разностные уравнения первого порядка. Как уже говорилось, цифровая система может содержать аналоговые и цифровые элементы, и, следовательно,

22

уравнения состояния в общем случае будут состоять одновременно из дифференциальных и разностных уравнений первого порядка. Однако не должно складываться впечатление, что использование метода пространства состояний для анализа и синтеза систем управления всегда имеет очевидные преимущества. Достоинство хорошо известного частотного метода состоит в его компактности, и большое число задач проектирования реальных систем управления по-прежнему решается с использованием методов синтеза, основанных на определении передаточной функции.

Линейные дискретные системы описываются линейными разностными уравнениями. Пусть математическая модель объекта управления имеет следующий вид:

x[k + 1] = (T0)x[k] + u[k]; (9.1) где x[k] – n-мерный вектор состояния объекта управления; (T0) – матрица размерности n n; (T0) – матрица входа размерности n 1; u[k] – управляющее воздействие.

Если уравнения динамики непрерывной линейной стационарной системы записаны в виде

x(t) = Ax(t) + Bu(t);

матрицы A и B имеют такую же размерность, как матрицы (T0) и(T0).

Тогда, подобно решению скалярных дифференциальных уравнений, решение обозначенного уравнения представляется в виде

x(t) = eA(t )x( );

где матрица (t) = eA(t) называется переходной матрицей состояния системы.

С использованием обратного преобразования Лапласа переходную матрицу состояния можно записать следующим образом:

h i

(t) = L 1 (sI A) 1 :

Для линейной цифровой системы матрицы (T0) и (T0) имеют вид

23

Z T0

(T0) = (T0 )B( )d : (9.2)

0

Подробно метод синтеза по заданному расположению полюсов с помощью обратной связи по состоянию (скалярное управление) подробно описан в разд. лекций 10.4.

Синтез системы регулирования объектом (9.1) сводится к поиску управляющего воздействия, которое обеспечивает в замкнутой систе-

где G – матрица обратной связи размерности 1 n. В общем виде она принимает вид

k (z) = [Adj (zI )] ;

где 0(z) = jzI j – характеристическое уравнение разомкнутой системы.

Пример. Рассмотрим пример синтеза управляющего воздействия

Введем обратную связь по состоянию, реализовав ее с помощью датчиков углового перемещения и скорости. Управление осуществля-

Задачей синтеза является определение g1 и g2 таким образом, чтобы замкнутая цифровая система управления имела собственные значения 1 = 2 = 0. Важно подчеркнуть, что собственные значения замкнутой системы являются собственными значениями матрицы

(T0) (T0) G:

24

Необходимо отметить, что объем вычислений при определении переходной матрицы состояния обычно больше, чем при решении линейного дифференциального уравнения относительно зависимой переменной. Однако имеющаяся дополнительная информация позволяет проектировщику системы управления использовать более совершенные методы проектирования.

Вычисление переходной матрицы состояния может выполняться несколькими способами:

–на теореме Сильвестра;

–на методе Кэли-Гамильтона;

–разложением в бесконечный ряд;

–на методе частотной области и т.д.

В данном случае удобно использовать метод Кэли-Гамильтона, который подробно описан в пособии Марченко Ю.Н. Конспект лекций по курсу ¾Теория автоматического регулирования¿ / Изд-во Новокузнецкого филиала-института Кемеровского государственного университета. – Новокузнецк, 2002. – С. 65-66.

Запишем характеристическое уравнение

Корни характеристического уравнения: 1 = 1; 2 = 2. Так как матрица A второго порядка, то многочлен R( ) первого порядка:

R( ) = 0 + 1 .

В нашем случае

e t = 0 1; e 2t = 0 2 1:

Откуда

0 = 2e t e 2t;1 = e t e 2t:

25

Найдем матрицу (T0) с использованием выражения (9.2):

Характеристическое уравнение разомкнутой системы:

Так как пара матриц [ , ] полностью управляема, то с помощью обратной связи по состоянию собственные значения матрицы G можно задать произвольным образом. Пусть желаемое характеристическое уравнение замкнутой системы имеет вид c (z) = z2 = 0.

Вычислить выражение k (z). Листинг программы в пакете Maple: >with(linalg):

>M:=matrix([[z-1,-0.005],[0.01,z-1]]); >ADJM:=adjoint(M); >Theta:=matrix([[0.00001],[0.005]]); >k:=evalm(ADJM&*Theta);

Матрицу обратной связи определим из соотношения (9.4)

26

Вычислим вектор G с использованием выражения (9.3) Листинг программы в пакете Maple:

>K:=matrix([[0.000015, 0.00001],[-0.005, 0.005]]); >invK:=inverse(K);

>Delta:=vector([1.015, -2]); >G:=-evalm(Delta&*invK);

G = 39400 321; 2 :

Таким образом, выражение для управляющего воздействия имеет вид

u [kT0] = 39400 x1 [kT0] 321; 2 x2 [kT0] :

9.2. Использование MatLab

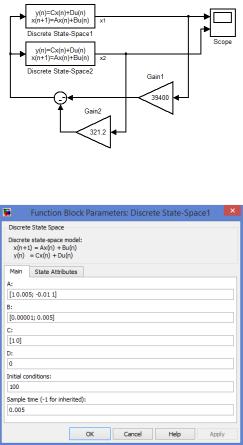
Провести моделирование цифровой части можно в пакете MatLab Simulink. Для этого удобно использовать блок Discrete State-Space (рис. 9.1). На вход данного блока подается управляющее воздействие.

Настройки блока Discrete State-Space1 приведены на рис. 9.2. На выходе данного блока мы получаем сигнал x1 [kT0]. Для того, чтобы получить сигнал x2 [kT0], необходимо дублировать блок и изменить параметр С (матрица выхода) с [1 0] на [0 1].

9.3. Задание к лабораторной работе

1.Осуществить синтез регулятора для объекта управления в соответствии с вариантом задания (см. табл. 9.1).

2.Собрать в MatLab Simulink структурную схему системы с дискретным модальным регулятором и проверить полученные результаты.

Отчет должен содержать:

– краткие теоретические сведения;

27

–расчетную часть;

–структурные схемы моделирования в Simulink;

–графики переходных процессов в системе;

–выводы.

Рис. 9.1. Схема синтезированной системы

Рис. 9.2. Настройки блокапараметров Discrete State-Space

Контрольные вопросы

1. Запишите стандартную форму уравнений в пространстве состояний. Поясните физический смысл уравнений.

28

2.Что представляет собой переходная матрица состояния систе-

мы?

3.Опишите вычисление переходной матрицы состояния системы методом Кэли-Гамильтона.

4.Как осуществить синтез регулятора для системы с несколькими управляющими воздействиями?

5.Как осуществить синтез регулятора с помощью обратной связи по выходу?

Варианты заданий

29