
LabTAU7-9
.pdf
УДК 681.51.01(07.07)
Составители: Радионов И.А., Мотиенко Т.А.
Методические указания к выполнению лабораторных работ № 7–9 по дисциплине ¾Теория автоматического управления¿. – Таганрог: Изд-во ЮФУ, 2014. – 30 с.
Представлен лабораторный практикум по ряду базовых разделов дисциплины ¾Теория автоматического управления¿. К каждой работе прилагаются краткие теоретические сведения и рекомендации по использованию пакета MATLAB.
Указания предназначены для студентов направления подготовки 27.03.03 ¾Системный анализ и управление¿.
Табл. 3. Ил. 8.
Рецензент С.В. Поликарпов, канд. техн. наук, доцент кафедры информационной безопасности телекоммуникационных систем ЮФУ.
7. МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ СИСТЕМ
Цель работы: исследование методов моделирования дискретных систем средствами Matlab (пакет Simulink).
7.1. Методические указания
Экстраполятор нулевого порядка
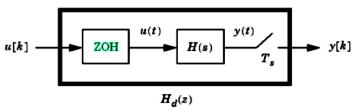
Дискретизация с экстраполятором нулевого порядка Hd(z) непрерывной LTI-модели H(s) изображена на следующей блок-схеме.
Рис. 7.1. Дискретизация с экстраполятором нулевого порядка
ZOH-устройство генерирует непрерывный входной сигнал u(t), поддерживая каждую величину u[k] постоянной в течение одного периода:
u (t) = u [k] ; kTs t (k + 1) Ts:
Сигнал u(t) подается непрерывной системе H(s), получающийся выход y(t) отбирается каждые Ts секунд, для формирования y[k].
Для данной дискретной системы Hd(z) преобразование d2c построит непрерывную систему H(s), чья ZOH-дискретизация совпадает с Hd(z). Это обратное действие имеет следующие ограничения:
–d2c не может работать с LTI-моделями с полюсами в z=0;
–отрицательные вещественные полюса в области s отображаются парой комплексных полюсов в области z. В результате преобразование d2c дискретной системы с отрицательными вещественными полюсами построит непрерывную систему с более высоким порядком.
Экстраполятор первого порядка
FOH отличается от ZOH механизмом экстраполяции. Для перевода входной последовательности и[к] в непрерывный вход u(t) FOH
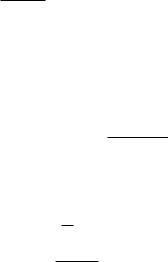
использует линейную интерполяцию:
u (t) = u [k] + t kTs (u [k + 1] u [k]) ; kTs t (k + 1) Ts: Ts
Этот метод является более точным, чем ZOH, для систем, управляемых гладкими входами.
Преобразование Тастина
Преобразование Тастина или билинейное преобразование описывается формулой
z= esTs 1 + sTs=2 1 sTs=2
ииспользуется для соотнесения передаточных функций в областях z
иs. В преобразовании с2d дискретизация Hd(z) непрерывной функ-
ции H (s) получается
Hd (z) = H (s0) ; где s0 = 2 z 1 :
Ts z+1
Аналогично преобразование полагается на обратное соответствие
H (s) = Hd (z0) где z0 = 1+sTs=2 :
1 sTs=2
Устойчивость и переходная характеристика
Для непрерывных систем поведение определяется расположением полюсов на s-плоскости. Например, система неустойчива, если полюса расположены в правой полуплоскости. Поведение дискретных систем можно анализировать, исходя из расположения полюсов на плоскости z. Характеристики плоскости z могут быть соотнесены с характеристиками плоскости s в соответствии с выражением:
z = esT ;
где T – время выборки; s – место на плоскости S; z – место на плоскости Z.
Мнимая ось (граница области устойчивости на плоскости S) переходит в окружность единичного радиуса (граница области устойчивости на плоскости Z) jzj = l. Система будет устойчивой, если все полюса расположены внутри единичной окружности, и неустойчивой, если хотя бы один полюс расположен вне ее.
Для анализа переходной характеристики применяются те же три уравнения, которые используются и для непрерывных систем:
4
! |
|
|
4:6 |
; ! |
|
1:8 |
; = v |
|
|
ln Mp/ |
2 |
|
|
; |
|
n |
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
n |
Tr |
u |
|
|
|
|
||||||
|
|
Ts |
u |
1 + |
ln Mp |
|
|
|
|
||||||
|
|
|
|
|
|
|
u |
/ |
|
|
|
||||
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
||
где – скорость затухания; !n – собственная частота (радиан/сек); Ts – время стабилизации; Tr – время нарастания; Mp – максимальное перерегулирование.
Собственная частота (!n) на плоскости z-plane измеряется в радиан/выборка, но при использовании приведенных выше уравнений в качестве единицы измерения Wn нужно брать радиан/с.
7.2. Использование MatLab
Использование функции c2d
ВMatlab существует функция c2d, отвечающая за преобразование заданной непрерывной системы в дискретную систему. В качестве моделей могут быть указаны TF, SS, или ZPK-модели. Функция d2c осуществляет обратное преобразование. Команда поддерживает несколько методов дискретизации, включая экстраполятор нулевого порядка (ZOH), экстраполятор первого порядка (FOH), а также приближение Тастина. Синтаксис:
1. Sysd = c2d (sysc, Ts), где Ts = период выборки; 2. Sysc = d2c (sysd).
Втаком виде команда выполняет ZOH-преобразование по умолчанию. Чтобы использовать альтернативные конверсионные схемы, следует определить желаемый метод как дополнительный параметр:
1. Sysd = c2d (sysc, Ts, ’foil’), где ’foil’ экстраполятор первого порядка;
2. Sysc = d2c (sysd, ’tustin’), где ’tustin’ приближение Тастина. Следующий пример иллюстрирует свойство d2c с реальными от-
рицательными полюсами. Рассмотрим модель ZPK: >> hd = zpk([], -0.5, 1, 0.1)
Zero/pole/gain:
1
5
(Z+0.5)
Sampling time: 0.1
Применим d2c для преобразования этой модели в непрерывную: >> hc = d2c(hd)
В результате получим модель второго порядка. Zero/pole/gain:
4.621(s+149.3)
(Sˆ2+13.86s+1035)
Если снова провести дискретизацию: >> c2d(hc, 0.1)
Получится оригинальная дискретная система (с сокращаемой парой полюс/нуль в z =-0.5):
Zero/pole/gain:
(Z+0.5)
(Z+0.5)ˆ2 Sampling time: 0.1
Можно изменить время квантования TF, SS, или ZPK-модели sys1, используя команду: Sys2 = d2d (sysl, Ts).
Новый период квантования Ts не должен быть кратным предыдущему. Реакцию на единичный скачок для систем с различным периодом квантования можно получить следующим образом:
>>h1 = tf ([1 0.4], [1 -0.7], 0.1);
>>h2 = d2d (hl, 0.25) ;
>>step (h1, ’–’, h2, ’–’)
Чтобы дискретизировать передаточную функцию
H (s) = e 0;25s |
10 |
|
s3 + 3s + 10 |
||
|
с использованием экстраполяции нулевого порядка и интенсивности замеров 10 Гц, следует выполнить:
>>h = tf (10 [, 1 3 10], ’inputdelay’, 0.25);
>>hd = c2d (рука, 0.1)
Это позволит получить дискретную передаточную функцию Transfer function:
6
0.01187 zˆ2 + 0.06408 z + 0.009721 z^(12)*
zˆ3 - 1.655 zˆ2 + 0.7408 z Sampling time: 0.1
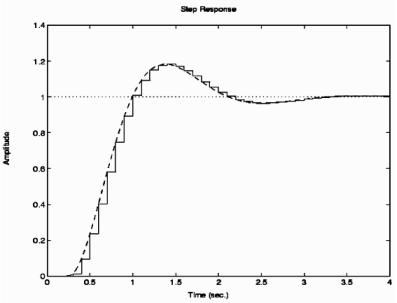
Здесь входная задержка в H (s) в 2.5 превышает период квантования в 0.1 секунды. Соответственно дискретизированная модель hd наследует входную задержку в два периода квантования, что подтверждается значением hd. Остаточная задержка размером в полупериод разделена в коэффициентах hd алгоритмом дискретизации. Реакции на скачок непрерывных и дискретизированных моделей сравниваются командой:
>> step(h, ’–’, hd, ’–’)
График приведен ниже на рис. 7.2.
Рис. 7.2. Реакции на скачок непрерывных и дискретизированных ПФ
Следует отметить, что преобразование Тастина только для задержек, которые кратны периоду квантования. Поэтому для моделей с задержками предпочтительно использовать zoh и foh методы дискре-
7

тизации.
Использование функции c2dm
Для построения дискретной модели заданной (в пространстве состояний или в форме передаточной функции) системы можно также использовать команду c2dm, записанную одним из следующих способов:
[numDz,denDz] = c2dm (num,den,Ts,’zoh’) [F,G,H,J] = c2dm (A,B,C,D,Ts,’zoh’)
Время Ts должно быть меньше 30BW1 , где BW – полоса частот замкнутой системы.
Пример: Пусть есть непрерывная передаточная функция
X (s) |
= |
1 |
; |
||
|
|
|
|
||
F (s) |
Ms2 + bs + k |
||||
где M = 1; b = 10; k = 20 F (s) = 1.
Приняв BW >1 рад/с, выберем Ts = 1=100 с. Теперь выполним следующие команды:
М=1;
b=10;
k=20;
num=[1]; den=[M b k]; Ts=l/100;
[numDz,denDz]=c2dm(num,den,Ts,’zoh’)
Получим следующие матрицы для числителя и знаменателя дискретной передаточной функции:
numDz = 1.0е-04 * 0 0.4837 0.4678 denDz =
1.0000 -1.9029 0.9048 Исходя из вида этих матриц, можно записать передаточную функ-
цию: |
|
|
|
|
X (s) |
= |
0; 0001 (0; 4837z + 0; 4678) |
: |
|
|
|
|
||
|
F (s) |
z2 1; 9029z + 0; 9048 |
||
8

Таким образом, была получена передаточная функция в дискретной форме.
Пример. Пусть есть следующая модель в пространстве состоя-
ний:
v |
= |
k/M |
b/M |
v |
+ |
1=M |
[F ] ; |
x |
|
0 |
1 |
x |
|
0 |
|
y = |
1 0 |
|
x |
+ [0] [F ] : |
v |
Все константы те же, что и раньше.
Приведенные ниже команды преобразовывают непрерывную модель в дискретную:
М=1;
b=10;
k=20;
А=[0 1;-к/М -b/М]; В=[0;1/М]; С=[1 0];
D=[0];
Ts=l/100;
[F,G,H,J] = c2dm(A,B,C,D,Ts,’zoh’)
Запуск этого кода в командном окне Matlab приведет к получению следующих матриц:
F =
0.9990 0.0095 -0.1903 0.9039 G = 0.0000 0.0095
H = 1 0 J = 0
Исходя из вида матриц, можно получить дискретную форму модели:
v (k) |
|
0; 1903 |
0; 9039 |
|
v (k 1) |
|
|
0; 0095 |
|
|
|
|
x (k) |
= |
0; 9990 |
0; 0095 |
|
x (k 1) |
+ |
|
0 |
|
[F (k |
|
1)] ; |
9
y (k |
|
1) = |
1 0 |
|
x (k 1) |
+ [0] [F (k |
|
1)] : |
|
|
|
v (k 1) |
|
|
Таким образом, получена дискретная модель в форме пространства состояний.
Устойчивость и переходная характеристика
Пусть есть дискретная передаточная функция:
Y (z) |
1 |
|
|
|
= |
|
: |
F (z) |
z2 0; 3z + 0; 5 |
||
Запишем команды: numDz=[l]; denDz=[l -0.3 0.5]:
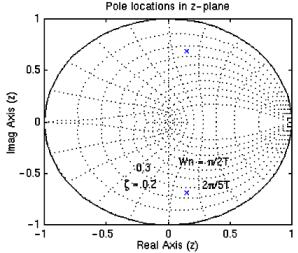
pzmap(numDz.denDz) axis([-l 1 -1 1])
zgrid
Рис. 7.3. Отображение нулей и полюсов ПФ
Запуск этого кода в командном окне приведет к отображению графика, изображенного на рис. 7.3:
10
