
- •Содержание:
- •1. Введение
- •1.1. Характеристики и параметры фильтров
- •1.2. Конструирование функций передачи фильтров
- •1.3. Синтез базовой матрицы низкочувствительных фильтров
- •2. Конверторные фильтры
- •2.1. Синтез лестничныхLc-фильтров
- •2.2. Конверторные фильтры нижних и верхних частот
- •2.3. Полосовые конверторные фильтры
- •3. Техническое задание
- •4. Структурная схема
- •5. Расчет элементов
- •6. Принципиальная схема
- •7. Анализ схемы
- •8. Метод монте-карло
- •9. Выбор типов элементов
- •10. Вывод
- •11. Список использемой литературы
2.3. Полосовые конверторные фильтры
Чтобы конверторная модель полосового
лестничного LC-фильтра
(см. рис. 2.3) не содержала избыточное
число реактивных элементов (конденсаторов),
все строки матрицы (2.8), за исключением
0-й строки у фильтров нечеткого порядка,
умножаются на оператор , в результате
чего схемы полосовых конверторных
фильтров четного (6-го) и нечетного (5-го)
порядков примут вид, показанный на рис.
2.10,аиб. В этих схемах
, в результате
чего схемы полосовых конверторных
фильтров четного (6-го) и нечетного (5-го)
порядков примут вид, показанный на рис.
2.10,аиб. В этих схемах –i-й
конвертор сопротивления с двумя
конденсаторами
–i-й
конвертор сопротивления с двумя
конденсаторами и
и (
( );
); – резисторы,
имитирующие соответствующие катушки
индуктивности схемы рис. 2.3;
– резисторы,
имитирующие соответствующие катушки
индуктивности схемы рис. 2.3; – резисторы,
которые совместно сi-м
иj-м конверторами
имитируют соответствующие конденсаторы
схемыLC-фильтра
(заземленный конденсатор
– резисторы,
которые совместно сi-м
иj-м конверторами
имитируют соответствующие конденсаторы
схемыLC-фильтра
(заземленный конденсатор реализуется
одним конвертором
реализуется
одним конвертором совместно с
резистором
совместно с
резистором );
); и
и – это
преобразованные
– это
преобразованные и
и . В схеме фильтра
четного порядка (рис. 2.10,а) входная
суперемкость
. В схеме фильтра
четного порядка (рис. 2.10,а) входная
суперемкость (емкость
(емкость LC-фильтра)
реализуется конвертором
LC-фильтра)
реализуется конвертором совместно с
конденсатором
совместно с
конденсатором . Конвертор
. Конвертор , в отличие от
, в отличие от , содержит один
конденсатор
, содержит один
конденсатор и три резистора
и три резистора ,
, ,
, .
.
Составив матрицу проводимостей схемы конверторного фильтра (используя матрицу подсхемы рис. 2.7), путем сопоставления элементов этой матрицы и соответствующей матрицы LC-фильтра можно получить соотношения, связывающие параметры элементов этих схем:
 (2.14)
(2.14)
где
 – центральная
частота фильтра;
– центральная
частота фильтра; – денормирующее
сопротивление;
– денормирующее
сопротивление; – параметр,
одинаковый для всех конверторов
– параметр,
одинаковый для всех конверторов ; параметр
; параметр относится
только к фильтру нечетногопорядка,
а параметры, отмеченные «*» в верхнем
индексе, – только к фильтру четного
порядка;
относится
только к фильтру нечетногопорядка,
а параметры, отмеченные «*» в верхнем
индексе, – только к фильтру четного
порядка; и
и ;
; и
и ;
; и
и ;
; и
и ;
; и
и ;
; и
и .
.

Рис. 2.10. Полосовые конверторные фильтры:
а – 6-го порядка; б – 5-го порядка
Если полосовой LC-прототип
(см. рис. 2.3) оптимизирован по величине
коэффициентов динамической перегрузки , то и его
конверторная модель (рис. 2.10) не будет
иметь динамических перегрузок вκ-х
(1,2, …) узлах. Однако на выходах
операционных усилителей, составляющих
конверторы сопротивления,
, то и его
конверторная модель (рис. 2.10) не будет
иметь динамических перегрузок вκ-х
(1,2, …) узлах. Однако на выходах
операционных усилителей, составляющих
конверторы сопротивления, дБ (
дБ ( ).
Оптимизация
).
Оптимизация выполняется
на этапе расчета схемы конверторного
фильтра путем соответствующего выбора
параметров элементов конверторов.
выполняется
на этапе расчета схемы конверторного
фильтра путем соответствующего выбора
параметров элементов конверторов.
3. Техническое задание
C0610с;
Исходные данные содержатся в таблице 5.13.
Таблица 5.13
|
|
|
|
|
|
|
|
|
30 0,0800718 |
2,12408 1,5578596 |
72,73 0,1398629 |
1,3648140 1,3662128 |
1,4828197 |
0,8995567 |
0,8231179 |
Граничная частота полосы пропускания
 кГц.
кГц.
 рад/с.
рад/с.
4. Структурная схема
Руководствуясь (рис. 2.1,а) и соотношениями (2.5), составим схемуLC-фильтра 6-го порядка

Рис.2.8.1 Схема лестничногоLC- фильтр 6-го порядка

Рис.2.8.2 Схема конверторного ФВЧ 6-го порядка
5. Расчет элементов
Связь между параметрами элементов конверторного ФНЧ-А (рис. 2,б) и параметрами элементов LC-ФНЧ-прототипа (рис. 2,а) описывается базовыми соотношениями (2.11), на основании которых, используя соотношения (2.5), можно выполнить расчет схемы (рис.2,б) в указанной ниже последовательности.
а)
Зададимся денормирующим сопротивлением
![]() и вычислим
и вычислим
 .
.
 =
52.879 кОм
=
52.879 кОм
При выборе значения
 учитываем
наличие такого значения в ряду номинальных
значений, а также технологические и
эксплуатационные ограничения на
минимальные и максимальные значения
параметров резисторов и конденсаторов.
Поскольку для фильтров типаaиc
учитываем
наличие такого значения в ряду номинальных
значений, а также технологические и
эксплуатационные ограничения на
минимальные и максимальные значения
параметров резисторов и конденсаторов.
Поскольку для фильтров типаaиc , емкость
, емкость равна емкости
равна емкости .
.
б) Рассчитаем сопротивления резисторов, имитирующих индуктивности схемы LC-фильтра:
 ,
,
где
 ;
; при четномnи
при четномnи приn
нечетном.
приn
нечетном.
 *103
*103
 *103
*103
 *103
*103
 *103
*103
 *103
*103
Если для всех
конверторов задать одинаковые значения
сопротивлений
 и одинаковые
емкости
и одинаковые
емкости , то сопротивление
резистора
, то сопротивление
резистора i-го
конвертора (
i-го
конвертора ( )
определится из соотношения
)
определится из соотношения

(схема конвертора сопротивления приведена на рис. 2.4).
R22к *103(R8 см. рис.3)
*103(R8 см. рис.3)
R44к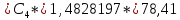 *103(R12 см. рис.3)
*103(R12 см. рис.3)
R66к *103(R16 см. рис.3)
*103(R16 см. рис.3)
Сопротивление резистора
 , шунтирующего
конденсатор
, шунтирующего
конденсатор , выбираем из
условия
, выбираем из
условия , а сопротивление
резистора
, а сопротивление
резистора , включенного
параллельно конденсатору
, включенного
параллельно конденсатору , вычислим из
соотношения
, вычислим из
соотношения
 либо
либо
 ,
,
что непринципиально,
если сопротивление неинвертирующего
входа ОУ ,
а точнее
,
а точнее
 , гораздо больше
, гораздо больше (
( ).
Поскольку на этом этапе проектирования
тип ОУ не выбран, предварительно примем
).
Поскольку на этом этапе проектирования
тип ОУ не выбран, предварительно примем .
Сопротивления
.
Сопротивления
 и
и уточним при
экспериментальном исследовании фильтра
(п. 5).
уточним при
экспериментальном исследовании фильтра
(п. 5).
 =4490,2224*103
=4490,2224*103
д)
Чтобы подключение внешней нагрузки
не привело к изменению параметров
фильтра, эта нагрузка должна подключаться
через буферный усилитель (рис. 5.2).
Поскольку номинальный коэффициент
передачи конверторного
фильтра (КФ), как и LC-прототипа,
равен 0,5 ( ),
путем задания одинаковых значений
сопротивлений в цепи отрицательной
обратной связи ОУ (
),
путем задания одинаковых значений
сопротивлений в цепи отрицательной
обратной связи ОУ ( )
можно повысить его до единицы.
)
можно повысить его до единицы.
В фильтрах четного порядка можно обойтись без буферного усилителя, снимая выходной сигнал фильтра с зажима 4 выходного конвертора (см. рис. 2.4), однако при этом ухудшаются частотные свойства этого конвертора, что сказывается на частотных свойствах всего фильтра.
е)
Результаты расчета фильтра с
граничной частотой кГц:
кГц:
 пФ,
пФ,
 *103,
*103,
 ,
, ,
, ,
, ,
, *103,
*103,
 ,
, ,
, ,
, *103,
*103,
 .
.
3. Поскольку параметры
 известны, а
известны, а дБ получили в
результате расчета буферного усилителя,
остается определить только граничную
частоту полосы режекции из выражения
дБ получили в
результате расчета буферного усилителя,
остается определить только граничную
частоту полосы режекции из выражения
 .
.
Внесем эти данные в строку “Расчетные” табл. 5.7.







