2.3. Геометрические вероятности

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l /Длина L.

Естественно, что геометрическую интерпретацию можно проводить не только на отрезке. Пусть плоская фигура D расположена в области . В области  случайно выбирается точка Х. Этот выбор можно интерпретировать, как бросание точки Х в область D. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке области , вероятность попадания брошенной точки на фигуру D пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно , ни от формы D. При этом попадание точки в область  – достоверное событие, а в D – случайное. Полагая, что все точки области  равноправны, все элементарные события являются равновозможными.

Рис. 2.1. Диаграмма области D

Пусть событие A = {XD}, то есть точка принадлежит области D, то геометрическая вероятность события А определится отношением площади D к площади 

. (2.1)

Если области  и D – линейны или объемны, то в этом случае

,

где l – длина, а V – объем соответствующей области.

Геометрическая вероятность обладает всеми свойствами, присущими классическому (и другим) определению:

1. Геометрическая вероятность любого события заключена между нулем и единицей, то есть

0  Р(А)  1.

2. Геометрическая вероятность невозможного события равна нулю, то есть

Р() = 0.

3. Геометрическая вероятность достоверного события равна единице, то есть

Р() = 1.

4. Геометрическая вероятность суммы несовместимых событий равна сумме вероятностей этих событий, то есть если АВ = , то

Р(А +В) = Р(А) + Р(В).

Пример. На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Решение. Разобьем отрезок ОА точками С и D на 3 равные части. Требование задачи будет выполнено, если точка В(х) попадет на отрезок CD длины L/3. Искомая вероятность P=(L/3)/L = l/3.

Пример. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Решение. Площадь кольца (фигуры g)

S_g = (10² – 5²) = 75.

Площадь большого круга (фигуры G)

S_G = 10² = 100.

Искомая вероятность

.

Пример. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t (t < T). Найти вероятность того, что сигнализатор сработает за время Т, если каждое из устройств пошлет по одному сигналу.

Решение. Обозначим моменты поступления сигналов первого и второго устройств соответственно через х и у. В силу условия задачи должны выполняться двойные неравенства: (0  x  T, 0  y  T,). Введем в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки квадрата ОТAT (рис. 2.2). Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов поступления сигналов.

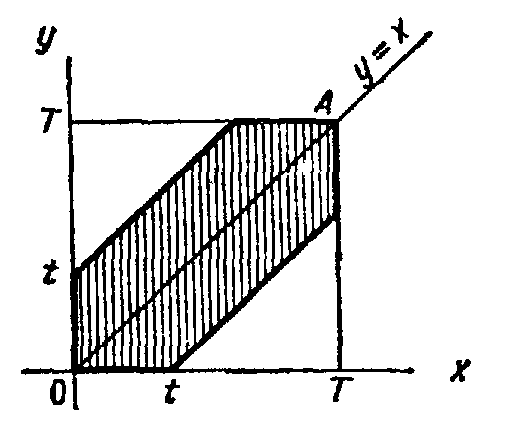
Рис. 2.2

Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t, т.е. если у – х < t при у > х и х – у < t при x > у, или, что то же,

y < x + t при у > х, (2.2)

у > x – t при у < x. (2.3)

Неравенство (2.2) выполняется для тех точек фигуры G, которые лежат выше прямой у=х и ниже прямой y = x + t, неравенство (2.3) имеет место для точек, расположенных ниже прямой у = х и выше прямой у = х – t.

Как видно из рис. 2.2, все точки, координаты которых удовлетворяют неравенствам (2.2) и (2.3), принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими моментами времени х и у.

Искомая вероятность

.

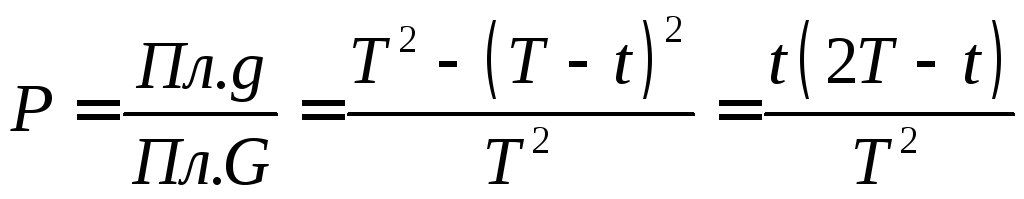Пример. В круг радиусом R вписан правильный треугольник. Найти вероятность тог, что точка, брошенная в этот круг, попадет в данный треугольник.

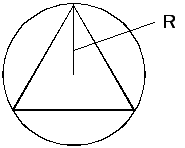
Рис. 2.3

Решение. .

Пример. Стержень разламывается на две части в случайной точке, равномерно распределенной по длине стержня. Найти вероятность того, что меньший обломок имеет длину, не превосходящую одной трети длины стержня.

Решение. Обозначим длину стержня l, а расстояние точки разлома от одного (фиксированного) конца стержня – х. Тогда описанное событие произойдет тогда и только тогда, когда либо х  l/3, либо x  2l/3. Искомая вероятность равна отношению (см. рис. 2.4).

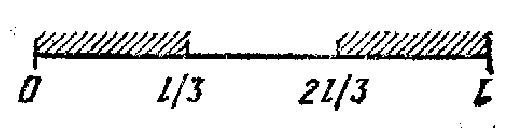
Рис. 2.4

Пример. Задача Бюффона. На плоскость, расчерченную параллельными прямыми, находящимися на расстоянии а друг от друга, случайно брошена игла длины l < a. Найти вероятность пересечения иглы с какой-нибудь из параллельных прямых.

Решение. Обозначим у расстояние от середины иглы до ближайшей прямой, х – острый угол между иглой и перпендикуляром к параллельным прямым (рис. 2.5). Координаты (х, у), определяющие положение иглы относительно параллельных прямых, удовлетворяют условиям 0  х  /2, 0  y  l/2. На плоскости (х, у) они образуют прямоугольник . Попадание точки (х, у) в заштрихованную область А (см. рис. 2.6) приводит к пересечению иглы с одной из параллельных прямых. По формуле (2.1) искомая вероятность равна

.

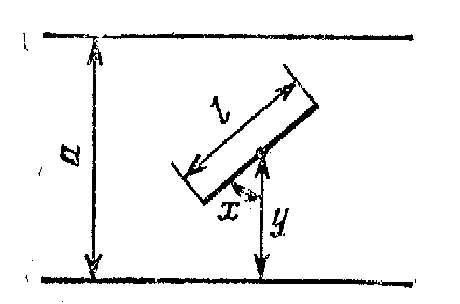
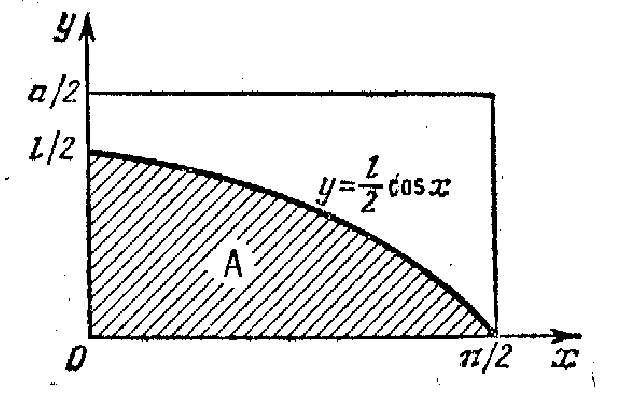
Рис. 2.5 Рис. 2.6

Замечание 1. Приведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область g – часть области G, равна

. (2.4)

Замечание 2. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.