7.10. Начальные и центральные теоретические моменты

Рассмотрим дискретную случайную величину X, заданную законом распределения:

X	1	2	5	100
р	0,6	0,2	0,19	0,01

Найдем математическое ожидание X:

М(X) = 10,6 + 20,2 + 50,19+ 100 0,01 =2,95.

Напишем закон распределения X²:

X2	1	4	25	10000
р	0,6	0,2	0,19	0,01

Найдем математическое ожидание X²:

М(X²) = 10,6 + 40,2 + 250,19 + 100000,01 = 106,15.

Видим, что М(X²) значительно больше М(X). Это объясняется тем, что после возведения в квадрат возможное значение величины X², соответствующее значению х = 100 величины X, стало равным 10 000, т.е. значительно увеличилось; вероятность же этого значения мала (0,01).

Таким образом, переход от М(X) к М(X²) позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина X имела несколько больших и маловероятных значений, то переход к величине X², а тем более к величинам X³, X⁴ и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).

Определение. Начальным моментом порядка k случайной величины X называют математическое ожидание величины X^k:

v_k = M(X^k).

В частности,

v₁ = M(X), v₂ = M(X²).

Пользуясь этими моментами, формулу для вычисления дисперсии D(X) = М(X²) – [М(X)]² можно записать так:

. (7.5)

Кроме моментов случайной величины X целесообразно рассматривать моменты отклонения X – М(X).

Определение. Центральным моментом порядка k случайной величины X называют математическое ожидание величины (X – М(X))^k:

.

В частности,

. (7.6)

. (7.7)

Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (7.5) и (7.7), получим

.

Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы:

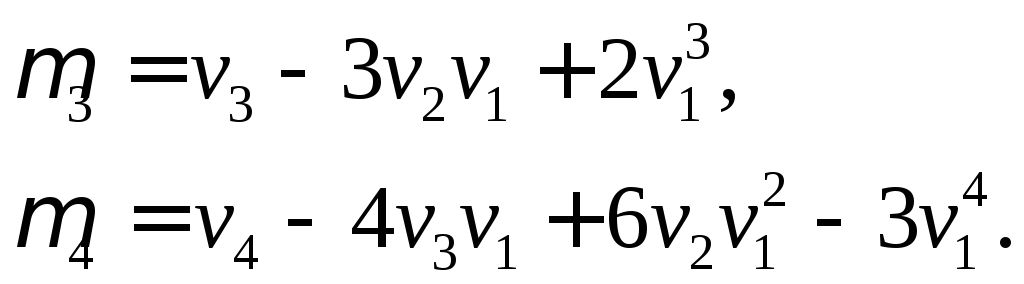
Моменты более высоких порядков применяются редко.

Замечание. Моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.

8. Закон больших чисел

8.1. Предварительные замечания

Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли (имеются и другие теоремы, которые здесь не рассматриваются). Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим. Для доказательства этих теорем мы воспользуемся неравенством Чебышева.