12.2. Вероятность попадания в заданный интервал показательно распределенной случайной величины
Найдем вероятность попадания в интервал (а, и) непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения
.
Используем
формулу (??)
.
Учитывая, что
,
,
получим
. (12.1)
Значения функции е–х находят по таблице.
Пример. Непрерывная случайная величина X распределена по показательному закону
.
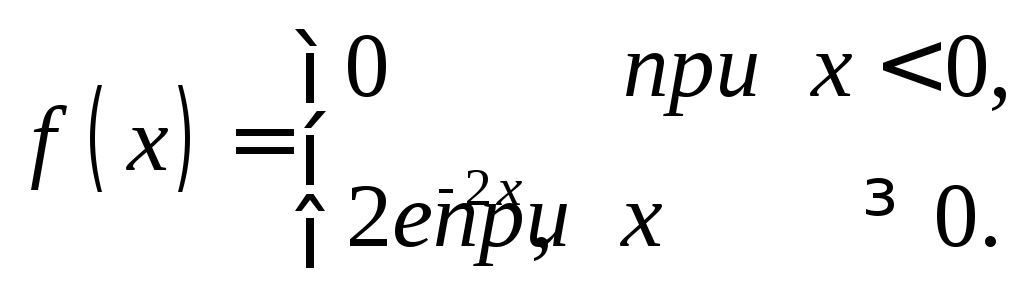Найти вероятность того, что в результате испытания X попадает в интервал (0,3, 1).
Решение. По условию, = 2. Воспользуемся формулой (12.1):
§ 3. Числовые характеристики показательного распределения
Пусть непрерывная случайная величина X распределена по показательному закону
.
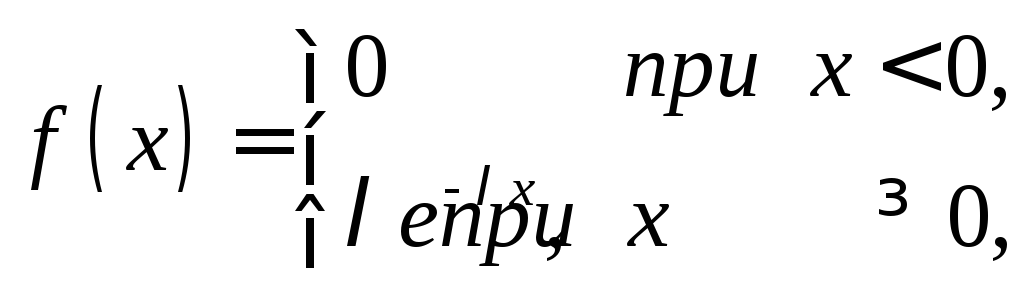Найдем математическое ожидание:
.
Интегрируя по частям, получим
. (12.2)
Таким образом, математическое ожидание показательного распределения равно обратной величине параметра X.
Найдем дисперсию:
.
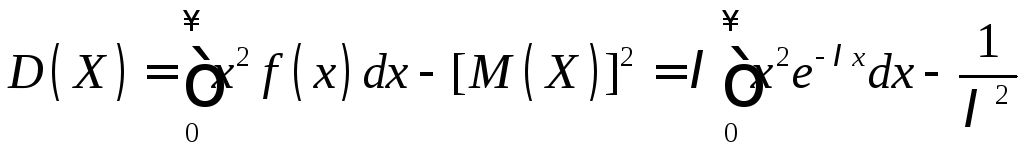Интегрируя по частям, получим
.
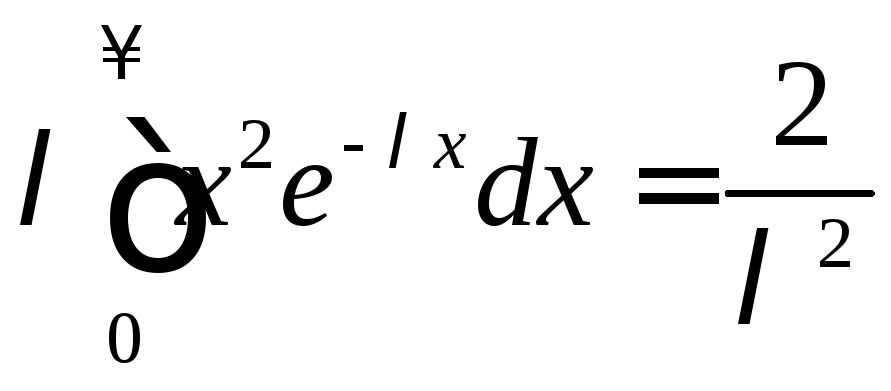Следовательно,
.
Найдем среднее квадратическое отклонение,
для чего извлечем квадратный корень из
дисперсии:
. (12.3)
Сравнивая
(12.2) и (12.3), заключаем, что
,
т.е. математическое ожидание и среднее
квадратическое отклонение показательного
распределения равны между собой.
Пример. Непрерывная случайная величина X распределена по показательному закону
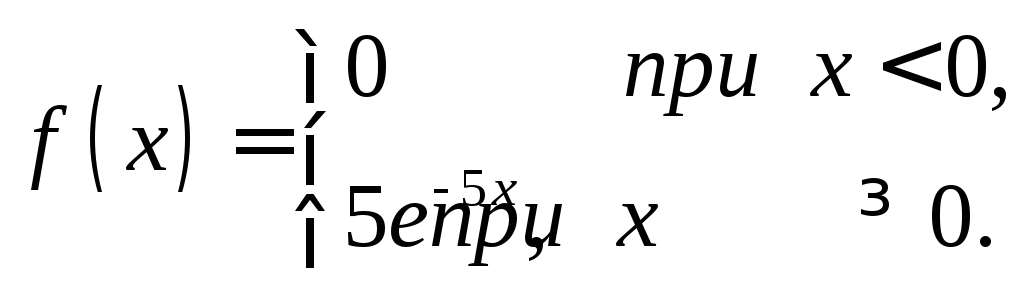
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Решение.
По условию,
= 5. Следовательно,
;
.
Замечание
1. Пусть на практике изучается показательно
распределенная случайная величина,
причем параметр
неизвестен. Если математическое ожидание
также неизвестно, то находят его оценку
(приближенное значение), в качестве
которой принимают выборочную среднюю
.
Тогда приближенное значение параметра
находят с помощью равенства
.
Замечание 2. Допустим, имеются основания предположить, что изучаемая на практике случайная величина имеет показательное распределение. Для того чтсбы проверить эту гипотезу, находят оценки математического ожидания и среднего квадратического отклонения, т.е. находят выборочную среднюю и выборочное среднее квадратическое отклонение. Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой, поэтому их оценки должны различаться незначительно. Если оценки окажутся близкими одна к другой, то данные наблюдений подтверждают гипотезу о показательном распределении изучаемой величины; если же оценки различаются существенно, то гипотезу следует отвергнуть.
Показательное распределение широко применяется в приложениях, в частности в теории надежности, одним из основных понятий которой является функция надежности.
12.4. Функция надежности
Будем называть элементом некоторое устройство независимо от того, «простое» оно или «сложное».
Пусть элемент начинает работать в момент времени t0=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t, то, следовательно, за время длительностью t наступит отказ.
Таким образом, функция распределения F(t) = P(T < t) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т.е. вероятность противоположного события Т > t, равна
. (12.4)
Функцией
надежности R(t)
называют функцию, определяющую вероятность
безотказной работы элемента за время
длительностью t:
.