11.13. Распределение «хи квадрат»

Пусть X_i (i = 1, 2, ..., n) – нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее ческое отклонение – единице. Тогда сумма квадратов этих величин

.

распределена по закону ² («хи квадрат») с k = n степенями свободы; если же эти величины связаны одним линейным соотношением, например , то число степеней свободыk = n – 1.

Плотность этого распределения

.

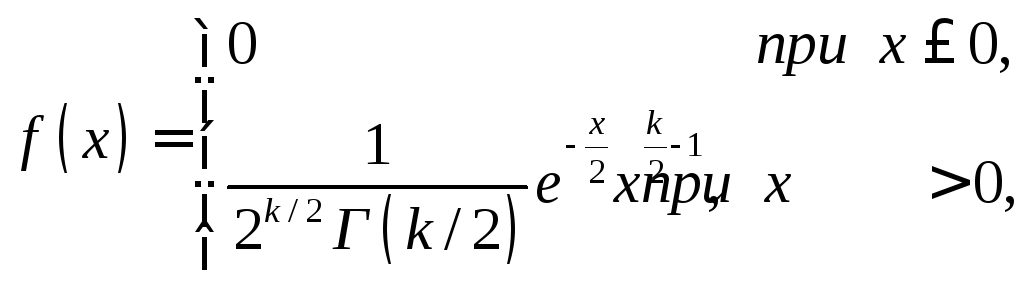где 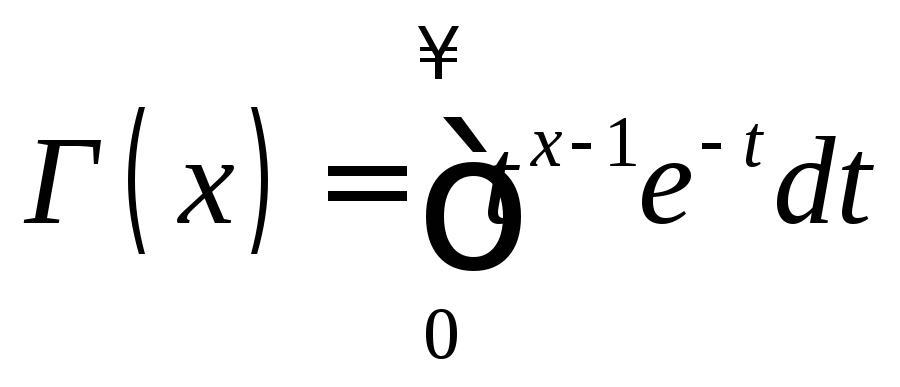– гамма-функция; в частности,

Г(x) = (n + 1) = n!.

Отсюда видно, что распределение «хи квадрат» определяется одним параметром – числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

11.14. Распределение Стьюдента

Пусть Z – нормальная случайная величина, причем M(Z) = 0, (Z) = 1, а V – независимая от Z величина, которая распределена по закону ² с k степенями свободы. Тогда величина

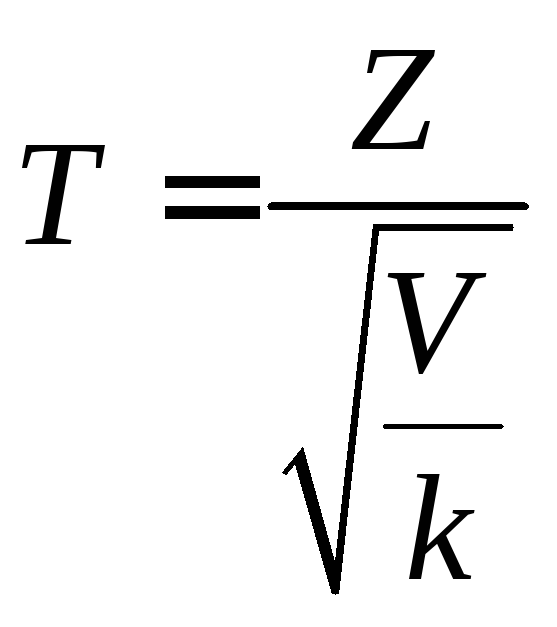(11.16)

имеет распределение, которое называют t-распределением или распределением Стьюдента (псевдоним английского статистика В. Госсета), с k степенями свободы.

Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

11.15. Распределение f Фишера – Снедекора

Если U и V – независимые случайные величины, распределенные по закону ² со степенями свободы k₁ и k₂, то величина

(11.17)

имеет распределение, которое называют распределением F Фишера–Снедекора со степенями свободы k₁ и k₂ (иногда его обозначают через V²).

Плотность этого распределения

.

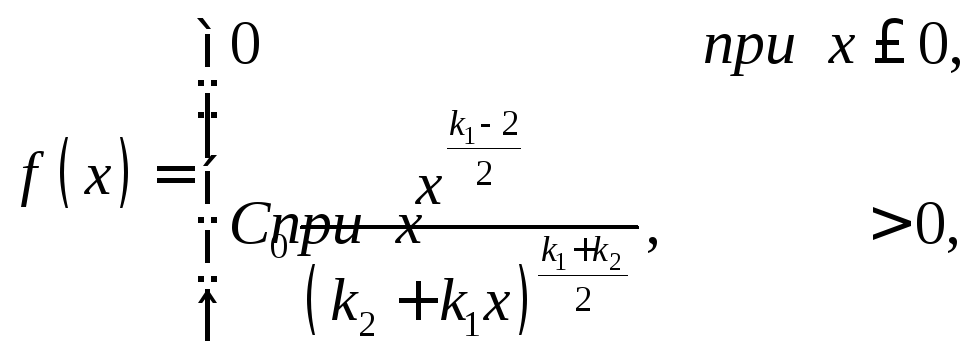где

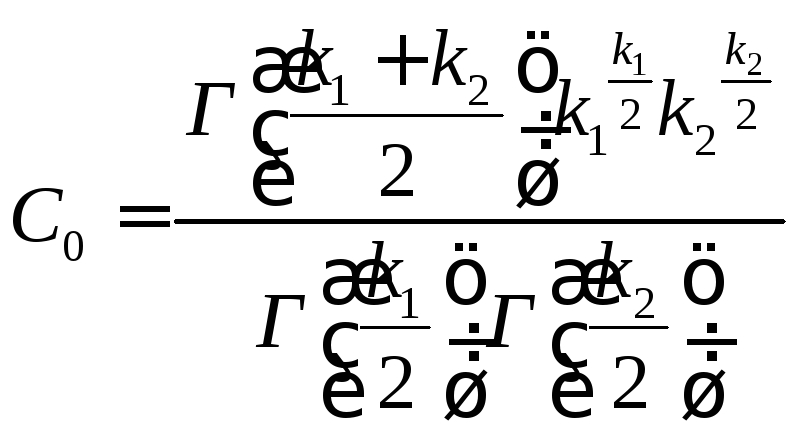
Видно, что распределение F определяется двумя параметрами – числами степеней свободы.

12. Показательное распределение

12.1. Определение показательного распределения

Определение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

.

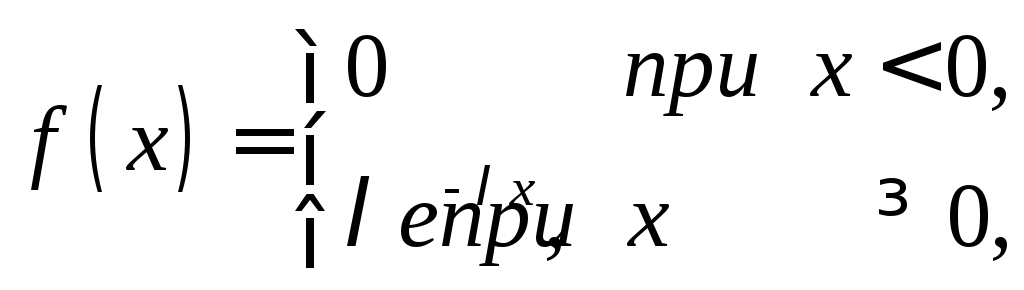где  – постоянная положительная величина.

Видно, что показательное распределение определяется одним параметром . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т.д. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.

Найдем функцию распределения показательного закона:

.

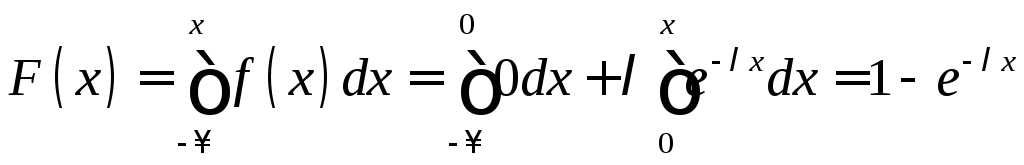Итак,

.

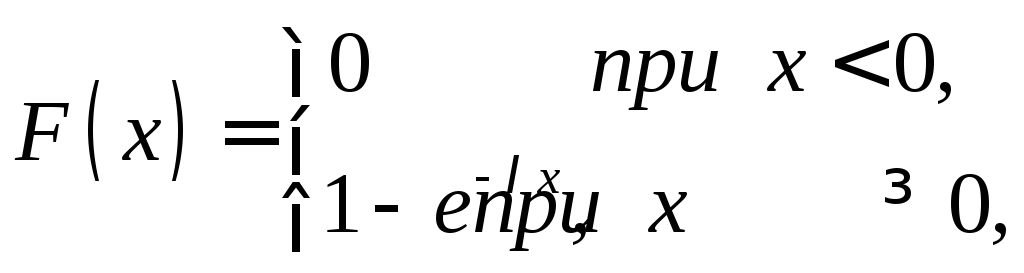Мы определили показательный закон с помощью плотности распределения; ясно, что его можно определить, используя функцию распределения.

Графики плотности и функции распределения показательного закона изображены на рис. 12.1.

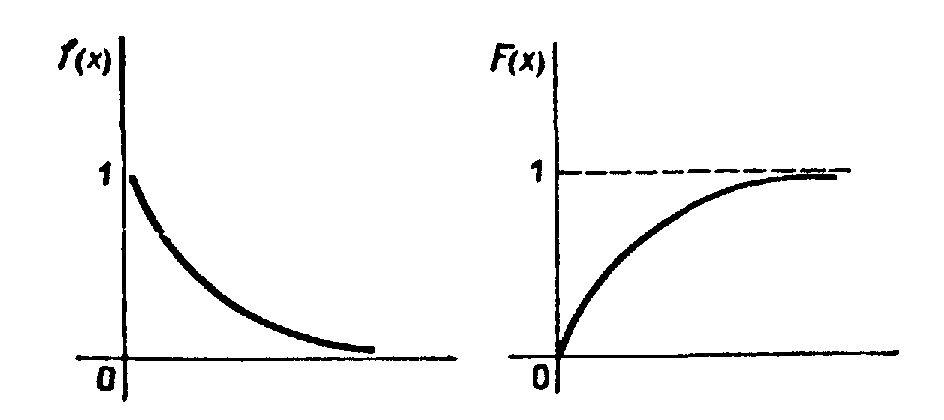
Рис. 12.1

Пример. Написать плотность и функцию распределения показательного закона, если параметр  = 8.

Решение. Очевидно, искомая плотность распределения

.

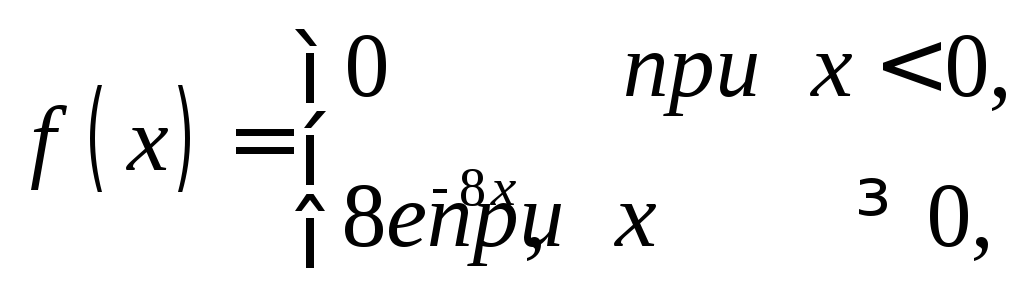Искомая функция распределения .
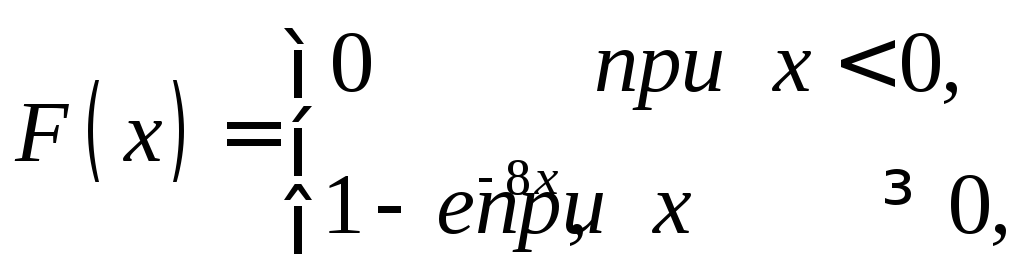