
- •Теория вероятностей и математическая статистика Основные понятия теории вероятностей Рекомендуемая литература
- •1.1. Предмет теории вероятностей
- •1.2. Области применения теории вероятностей
- •1.3. Краткая историческая справка
- •1.4. Испытания и события. Виды событий
- •1.5. Алгебра событий
- •1.6. Классическое определение вероятности
- •1.7. Основные формулы комбинаторики
- •Лекция №2. Основные понятия и определения
- •2.1. Относительная частота. Устойчивость относительной частоты
- •2.2. Ограниченность классического определения вероятности. Статистическая вероятность
- •2.3. Геометрические вероятности
- •2.4. Теорема сложения вероятностей
- •2.5. Полная группа событий
- •2.6. Противоположные события
- •2.7. Принцип практической невозможности маловероятных событий
- •2.8. Произведение событий. Условная вероятность
- •2.9. Теорема умножения вероятностей
- •2.10. Независимые события. Теорема умножения для независимых событий
- •2.10. Вероятность появления хотя бы одного события
- •Лекция №3 следствия теорем сложения и умножения
- •3.1. Теорема сложения вероятностей совместных событий
- •3.2. Формула полной вероятности
- •3.3. Вероятность гипотез. Формулы Бейеса
- •4. Повторение испытаний
- •4.1. Формула Бернулли
- •4.2. Предельные теоремы в схеме Бернулли
- •4.3. Локальная и интегральная теоремы Муавра-Лапласа
- •4.3. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
- •5. Случайные величины
- •5.1. Понятие случайной величины. Закон распределения случайной величины
- •5.2. Закон распределения дискретной случайной величины. Многоугольник распределения
- •5.3. Биномиальное распределение
- •5.4. Распределение Пуассона
- •5.5. Геометрическое распределение
- •5.6. Гипергеометрическое распределение
- •6. Математическое ожидание дискретной случайной величины
- •6.1. Числовые характеристики дискретных случайных величин
- •6.2. Математическое ожидание дискретной случайной величины
- •6.3. Вероятностный смысл математического ожидания
- •6.4. Свойства математического ожидания
- •6.5. Математическое ожидание числа появлений события в независимых испытаниях
- •7. Дисперсия дискретной случайной величины
- •7.1. Целесообразность введения числовой характеристики рассеяния случайной величины
- •7.2. Отклонение случайной величины от ее математического ожидания
- •7.3. Дисперсия дискретной случайной величины
- •7.4. Формула для вычисления дисперсии
- •7.5. Свойства дисперсии
- •7.6. Дисперсия числа появлений события в независимых испытаниях
- •7.7. Среднее квадратическое отклонение
- •7.8. Среднее квадратическое отклонение суммы взаимно независимых случайных величин
- •7.9. Одинаково распределенные взаимно независимые случайные величины
- •7.10. Начальные и центральные теоретические моменты
- •8. Закон больших чисел
- •8.1. Предварительные замечания
- •8.2. Неравенство Чебышева
- •8.3. Теорема Чебышева
- •8.4. Сущность теоремы Чебышева
- •8.5. Значение теоремы Чебышева для практики
- •8.6. Теорема Бернулли
- •Функция распределения вероятностей случайной величины
- •9.1. Определение функции распределения
- •9.2. Свойства функции распределения
- •9.3. График функции распределения
- •10. Плотность распределения вероятностей непрерывной случайной величины
- •10.1. Определение плотности распределения
- •10.2. Вероятность попадания непрерывной случайной величины в заданный интервал
- •10.3. Закон равномерного распределения вероятностей
- •11. Нормальное распределение
- •11.1. Числовые характеристики непрерывных случайных величин
- •11.2. Нормальное распределение
- •11.3. Нормальная кривая
- •11.4. Влияние параметров нормального распределения на форму нормальной кривой
- •11.5. Вероятность попадания в заданный интервал нормальной случайной величины
- •11.6. Вычисление вероятности заданного отклонения
- •11.7. Правило трех сигм
- •11.8. Понятие о теореме Ляпунова. Формулировка центральной предельной теоремы
- •11.9. Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс
- •11.10. Функция одного случайного аргумента и ее распределение
- •11.11. Математическое ожидание функции одного случайного аргумента
- •11.12. Функция двух случайных аргументов. Распределение суммы независимых слагаемых. Устойчивость нормального распределения
- •11.13. Распределение «хи квадрат»
- •11.14. Распределение Стьюдента
- •11.15. Распределение f Фишера – Снедекора
- •12. Показательное распределение
- •12.1. Определение показательного распределения
- •12.2. Вероятность попадания в заданный интервал показательно распределенной случайной величины
- •§ 3. Числовые характеристики показательного распределения
- •12.4. Функция надежности
- •12.5. Показательный закон надежности
- •12.6. Характеристическое свойство показательного закона надежности
11.10. Функция одного случайного аргумента и ее распределение
Предварительно заметим, что далее, вместо того чтобы говорить «закон распределения вероятностей», будем часто говорить кратко – «распределение».
Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X:
Y = (X).
Далее показано, как найти распределение функции по известному распределению дискретного и непрерывного аргумента.
1. Пусть аргумент X – дискретная случайная величина.
а) Если различным возможным значениям аргумента X соответствуют различные возможные значения функции Y, то вероятности соответствующих значений X и Y между собой равны.
Пример 1. Дискретная случайная величина X задана распределением
-
X
2
3
p
0,6
0,4
Найти распределение функции Y = X2.
Решение. Найдем возможные значения Y: у1 = 22 = 4; у2 = 32 = 9. Напишем искомое распределение Y:
-
Y
4
9
p
0,6
0,4
б) Если различным возможным значениям X соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.
Пример 2. Дискретная случайная величина X задана распределением
-
X
- 2
2
3
p
0,4
0,5
0,1
Найти распределение функции Y = X2.
Решение. Вероятность возможного значения у1 = 4 равна сумме вероятностей несовместых событий Х = - 2, Х = 2, т.е. 0,4 + 0,5= 0,9. Вероятность возможного значения у2 = 9 равна 0,1. Напишем искомое распределение Y:
-
Y
4
9
p
0,9
0,1
2. Пусть аргумент X – непрерывная случайная величина. Как найти распределение функции Y = (X), зная плотность распределения случайного аргумента X? Доказано: если y = (X) – дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой х = (у), то плотность распределения g(y) случайной величины Y находится с помощью равенства
![]() . (11.7)
. (11.7)
Пример 3. Случайная величина X распределена нормально, причем ее математическое ожидание а = 0. Найти распределение функции Y = Х3.
Решение. Так как функция y = x3 дифференцируема и строго возрастает, то можно применить формулу (11.7). Найдем функцию, обратную функции y = x3:
![]() .
.
Найдем
![]() .
По условию,
.
По условию,
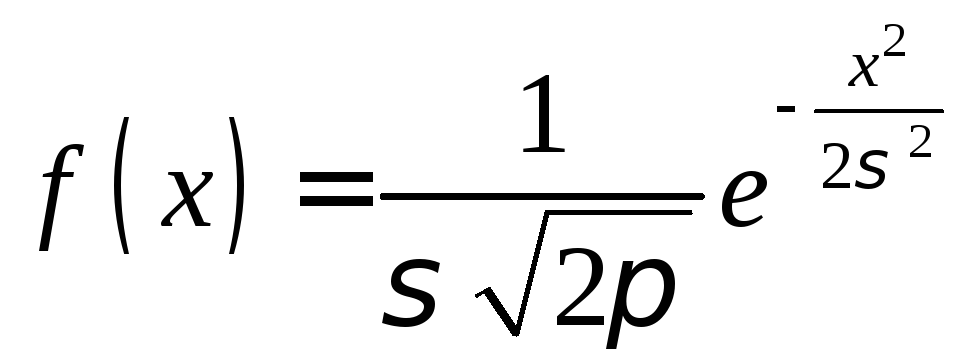 .
.
поэтому
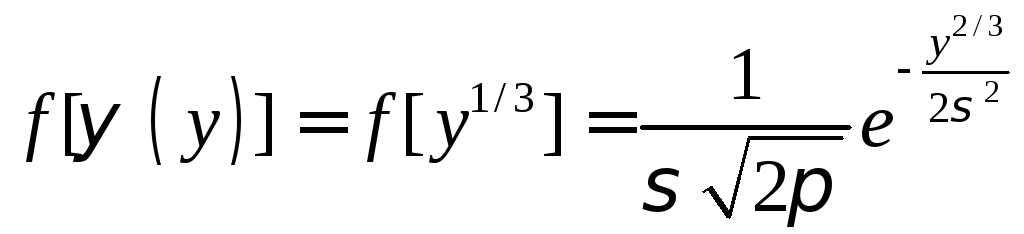 . (11.8)
. (11.8)
Найдем производную обратной функции по у:
![]() . (11.9)
. (11.9)
Найдем искомую плотность распределения, для чего подставим (11.) и (11.9) в (11.7):
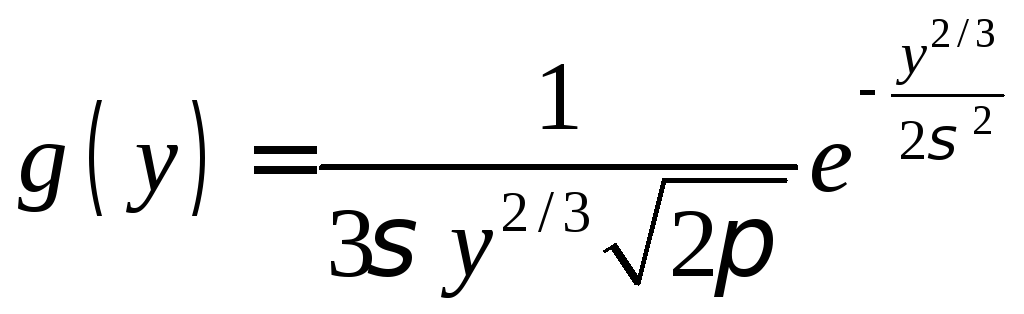 .
.
Замечание. Пользуясь формулой (11.7), можно доказать, что линейная функция Y = АХ + В нормально распределенного аргумента X также распределена нормально, причем для того чтобы найти математическое ожидание Y, надо в выражение функции подставить вместо аргумента X его математическое ожидание а:
М(Y) = Aa + B;
для того чтобы найти среднее квадратическое отклонение Y, надо среднее квадратическое отклонение аргумента X умножить на модуль коэффициента при X:
(Y) = |A| (X).
Пример 4. Найти плотность распределения линейной функции Y = 3Х + 1, если аргумент распределен нормально, причем математическое ожидание X равно 2 и среднее квадратическое отклонение равно 0,5.
Решение. Найдем математическое ожидание Y:
М(Y) = 32 + 1 = 7.
Найдем среднее квадратическое отклонение Y:
(Y) = 30,5 = 1,5.
Искомая плотность распределения имеет вид
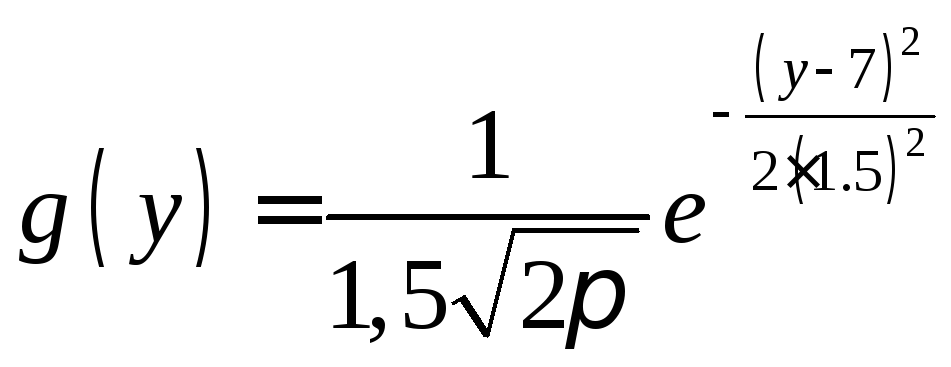 .
.
