11.4. Влияние параметров нормального распределения на форму нормальной кривой

Выясним, как влияют на форму и расположение нормальной кривой значения параметров а и . Известно, что графики функций f(х) и f(x – а) имеют одинаковую форму; сдвинув график f(х) в положительном направлении оси х на а единиц масштаба при а > 0 или в отрицательном направлении при а < 0, получим график f(x – а). Отсюда следует, что изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает.

По-иному обстоит дело, если изменяется параметр  (среднее квадратическое отклонение). Как было показано ранее, максимум дифференциальной функции нормального распределения равен . Отсюда следует, что с возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании  нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу.

Подчеркнем, что при любых значениях параметров а и  площадь, ограниченная нормальной кривой и осью х, остается равной единице.

На рис. 11.8 изображены нормальные кривые при различных значениях  и а = 0. Чертеж наглядно иллюстрирует, как изменение параметра  сказывается на форме нормальной кривой. Заметим, что при а = 0 и  = 1 нормальную кривую 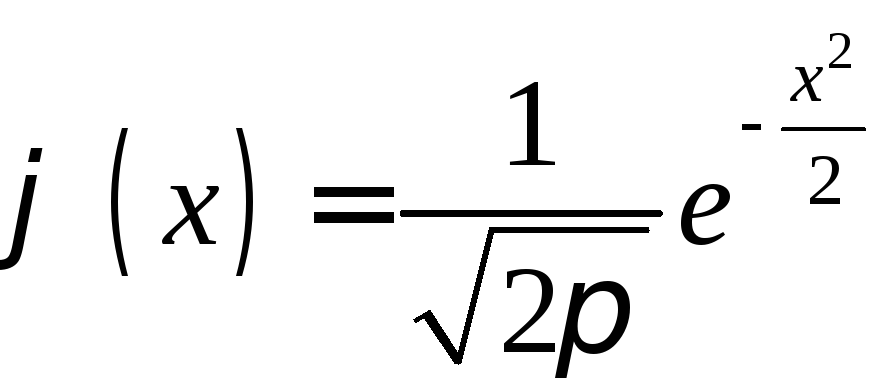называютнормированной.

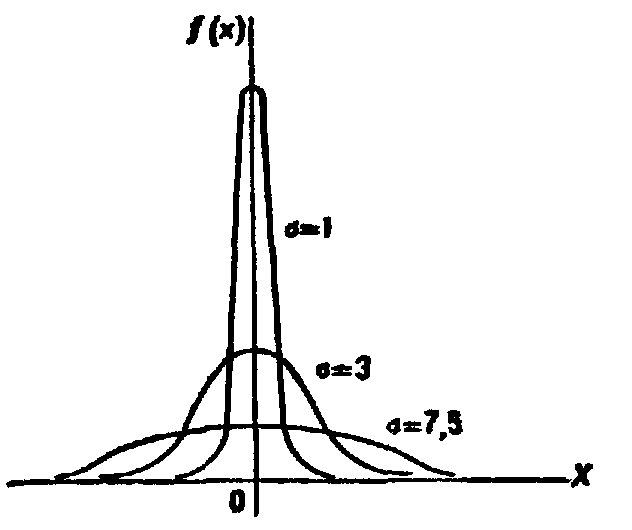
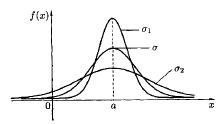
Рис. 11.8

Нормальному закону подчиняются ошибки измерений, величины износа деталей в механизмах, рост человека, ошибки стрельбы, вес клубней картофеля, величина шума в радиоприемном устройстве, колебания курса акций и т.д.

11.5. Вероятность попадания в заданный интервал нормальной случайной величины

Уже известно, что если случайная величина X задана плотностью распределения f(х), то вероятность того, что X примет значение, принадлежащее интервалу (, ), такова:

.

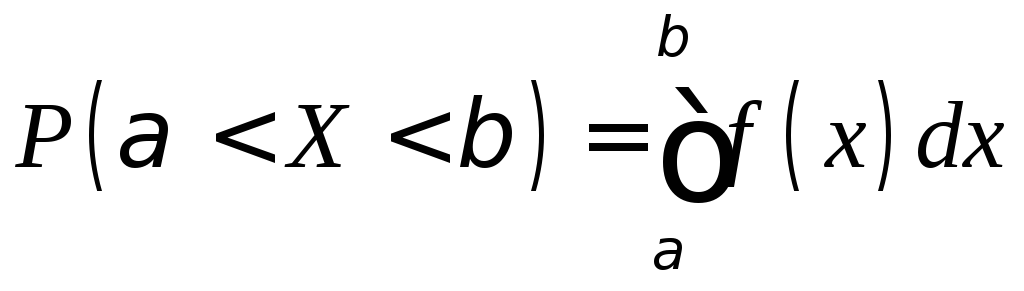Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (, ), равна

.

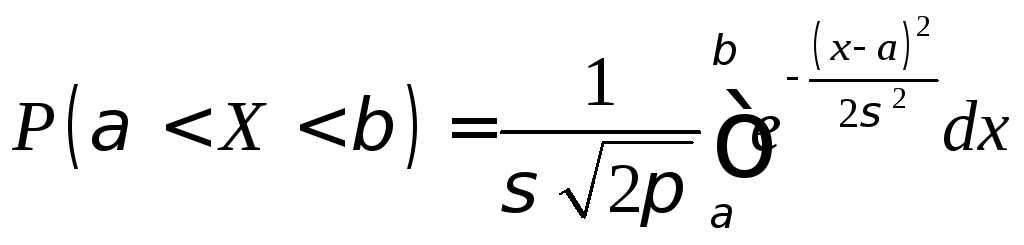Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную z = (x – а)/. Отсюда x = z + a, dx = dz. Найдем новые пределы интегрирования. Если х =, то z = ( – а)/; если х = , то z = ( – а)/.

Таким образом, имеем

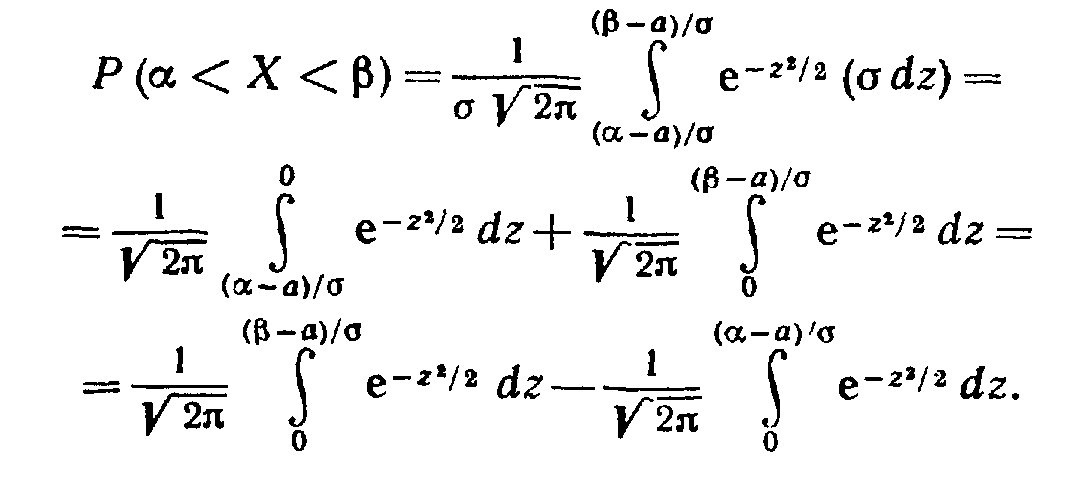
Пользуясь функцией Лапласа 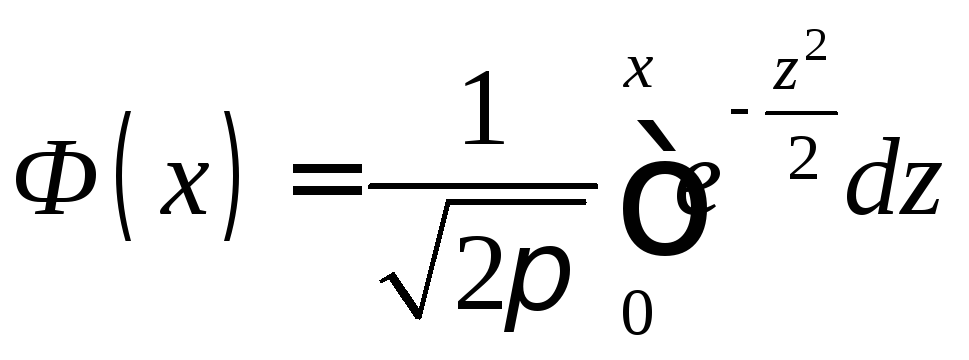окончательно получим

. (11.4)

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10, 50).

Решение. Воспользуемся формулой (11.4). По условию,  = 10,  = 50, а = 30,  = 10, следовательно,

.

По таблице приложения 2 находим Ф(2) = 0,4772. Отсюда искомая вероятность

Р(10 < X < 50) = 20,4772 = 0,9544.

11.6. Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа , т.е. требуется найти вероятность осуществления неравенства |Х – а| < .

Заменим это неравенство равносильным ему двойным неравенством

–  < Х – а < , или а –  < X < а + .

Пользуясь формулой (11.4), получим

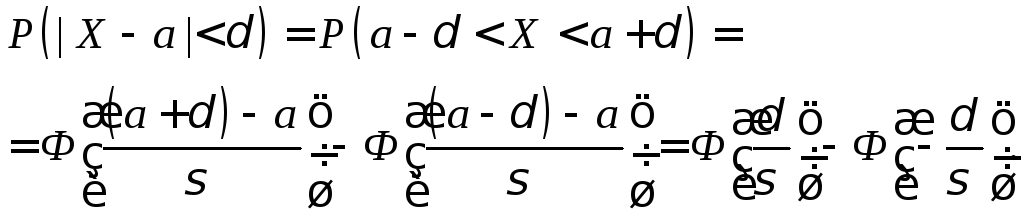
Приняв во внимание равенство (функция Лапласа – нечетная), окончательно имеем

. (11.5)

В частности, при а = 0

.

На рис. 11.9 наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (–, ), больше у той величины, которая имеет меньшее значение . Этот факт полностью соответствует вероятностному смыслу параметра  ( есть среднее квадратическое отклонение; оно характеризует рассеяние случайной величины вокруг ее математического ожидания).

Замечание. Очевидно, события, состоящие в осуществлении неравенств |X – а| <  и |Х – а|  , – противоположные. Поэтому, если вероятность осуществления неравенства |X – а| <  равна р, то вероятность неравенства |Х – а|   равна 1 – р.

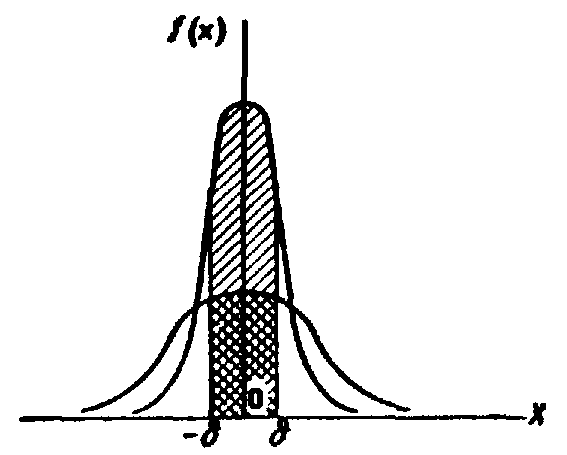
Рис. 11.9

Пример. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение X соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение. Воспользуемся формулой (11.5) . По условию, = 3, а = 20,  = 10. Следовательно,

.

По таблице приложения 2 находим Ф(0,3) = 0,1179. Искомая вероятность

.

Пример. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с параметром  = 10 мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.

Решение. По формуле (11.5) находим:

.

Вероятность того, что ошибка (погрешность) превышает 2 мм в одном опыте (измерении), равна

.

По теореме умножения вероятность того, что во всех трех опытах ошибка измерения превышает 2 мм, равная 0,84148³  0,5958. Следовательно, искомая вероятность равна 1 – 0,5958 = 0,4042.