10.3. Закон равномерного распределения вероятностей

При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений. Рассматрим закон равномерного распределения вероятностей.

Определение. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину X, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, X имеет равномерное распределение.

Найдем плотность равномерного распределения f(х), считая, что все возможные значения случайной величины заключены в интервале (а, b), на котором функция f(х) сохраняет постоянные значения. По условию, X не принимает значений вне интервала (а, b), поэтому f(х) = 0 при х < а и х > b.

Найдем постоянную С. Так как все возможные значения случайной величины принадлежат интервалу (а, b), то должно выполняться соотношение

.

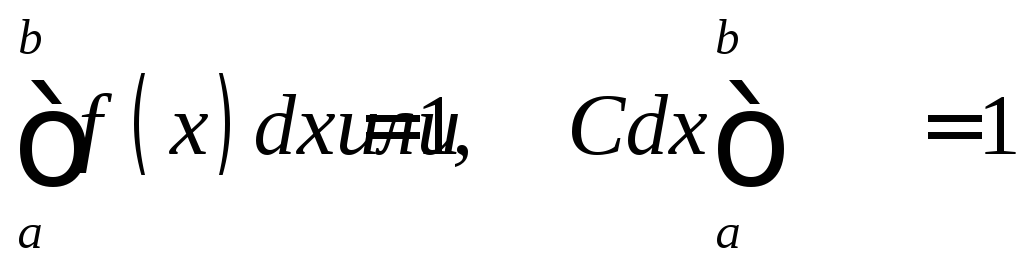Отсюда

.

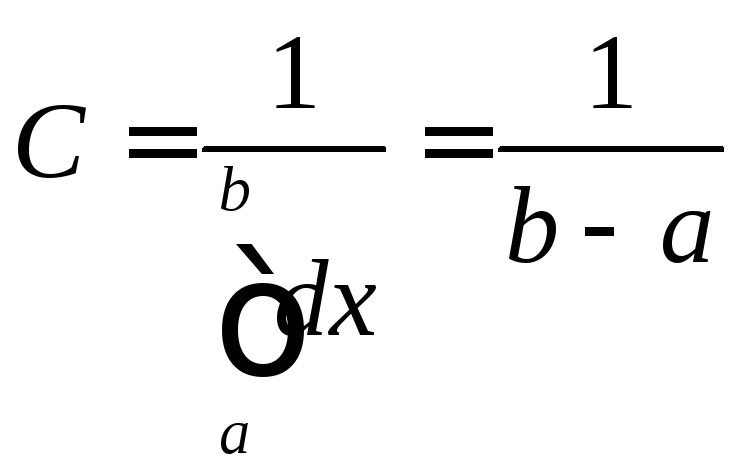Итак, искомая плотность вероятности равномерного распределения

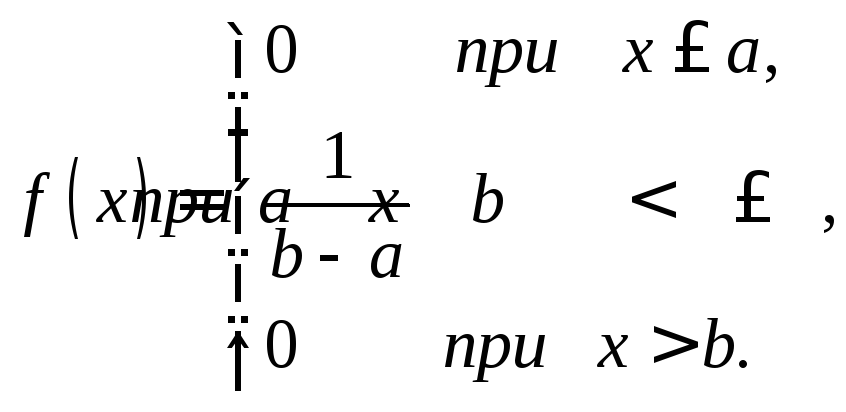
График плотности равномерного распределения изображен на рис. 10.4, а график функции распределения – на рис. 10.3.

Рис. 10.4

Замечание. Обозначим через R непрерывную случайную величину, распределенную равномено в интервале (0, 1), а через r – ее возможные значения. Beроятность попадания величины R (в результате испытания) в интервал (с, d), принадлежащий интервалу (0, 1), равна его длине:

Р(с < R < d) = d – c.

Действительно, плотность рассматриваемого равномерного распределения

f(r) = 1/(1 – 0) =1.

Следовательно, вероятность попадания случайной величины R в интервал (с, d)

.

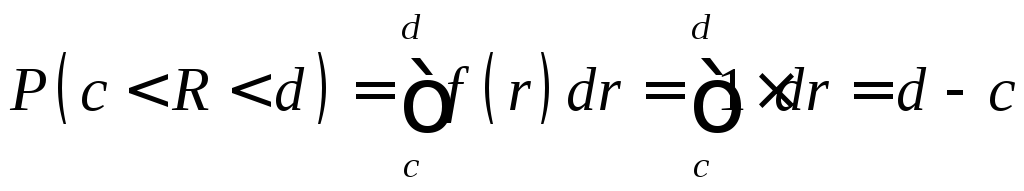Далее случайная величина R используется неоднократно.

К случайным величинам, имеющим равномерное распределение, относятся: время ожидания пассажиром транспорта, курсирующего с определенным интервалом: ошибка округления числа до целого (она равномерно распределена на отрезке [-0,5; 0,5]). И вообще случайные величины, о которых известно, что все ее значения лежат внутри некоторого интервала и все они имеют одинаковую вероятность (плотность).

Дискретная с.в.Х имеет равномерное распределение, если она принимает целочисленные значения 1, 2, 3, …, n с вероятностью p_m = P{X = m} = 1/n, где m = 1, 2, 3, …, n. В этом случае . Так приn = 5, многоугольник распределения имеет вид, представленный на рис. 10.5, M[X] = 3.

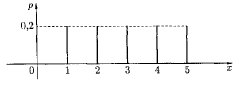
Рис. 10.5

11. Нормальное распределение

11.1. Числовые характеристики непрерывных случайных величин

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Пусть непрерывная случайная величина X задана плотностью распределения f(х). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот отрезок на n частичных отрезков длиной x₁, x₂, ..., x_n и выберем в каждом из них произвольную точку х_i (i = 1, 2, ..., n). Необходимо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений х_i на вероятности попадания их в интервал  х_i (напомним, что произведение f(х)x приближенно равно вероятности попадания X в интервал x):

.

Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл .

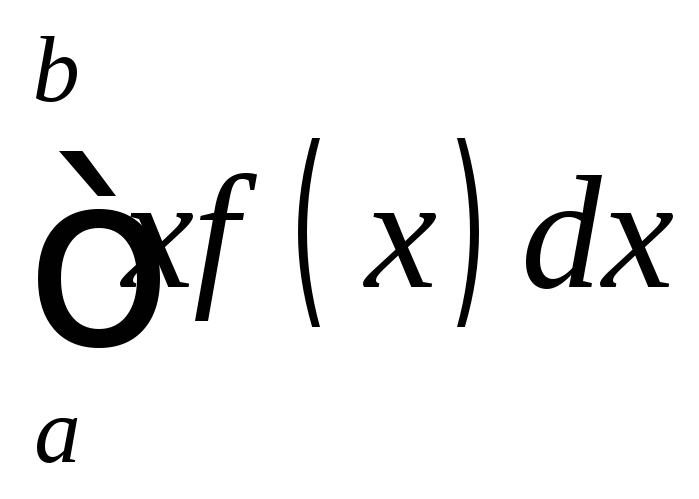Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл

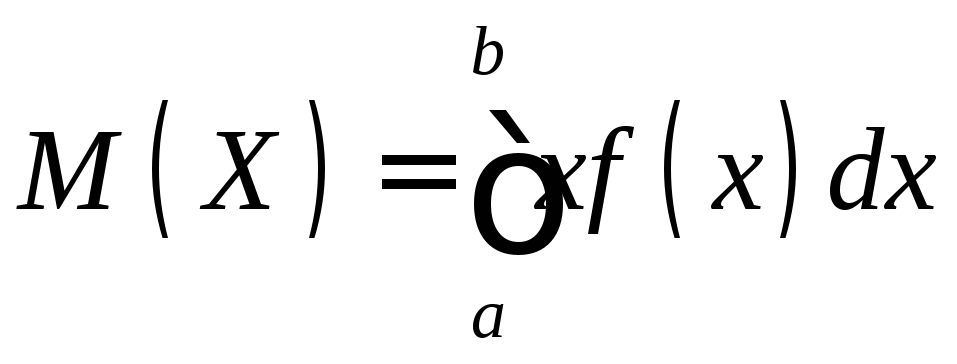. (11.1)

Если возможные значения принадлежат всей оси Ох, то

.

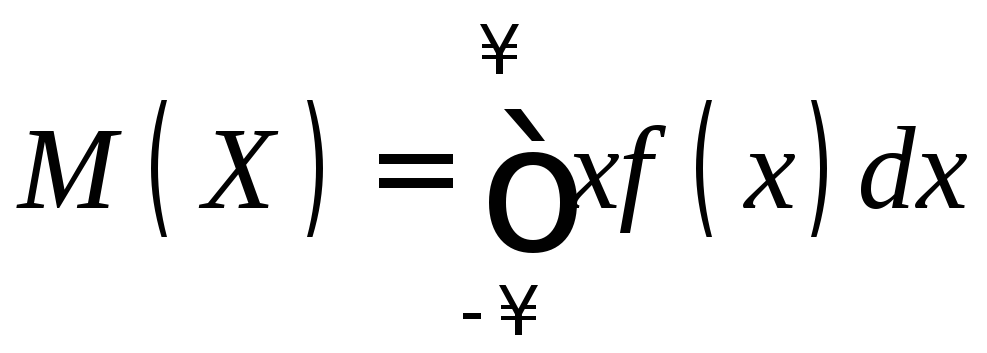Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл 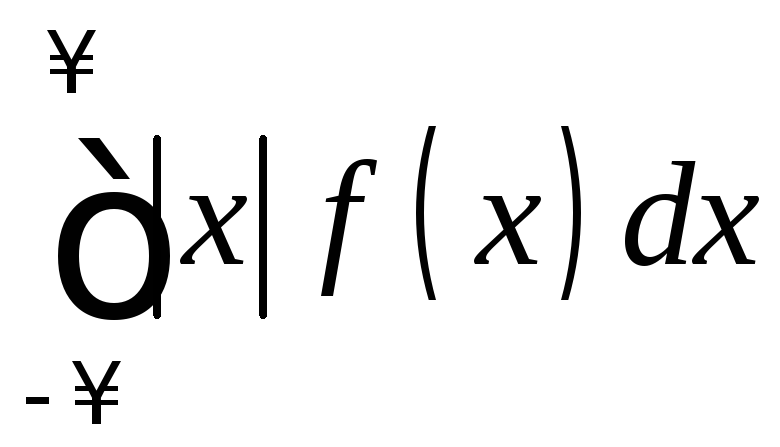. Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к –, а верхнего – к +.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Определение. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку [а, b], то

;

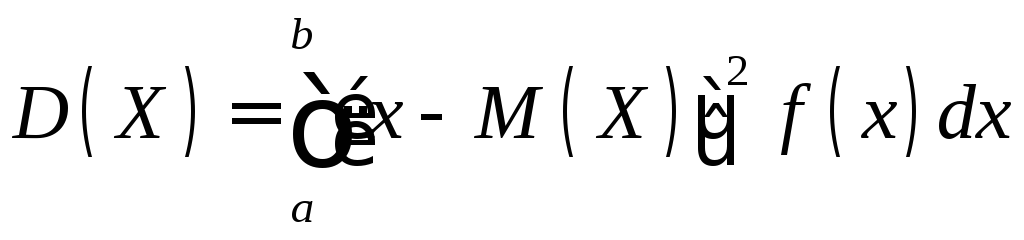если возможные значения принадлежат всей оси х, то

.

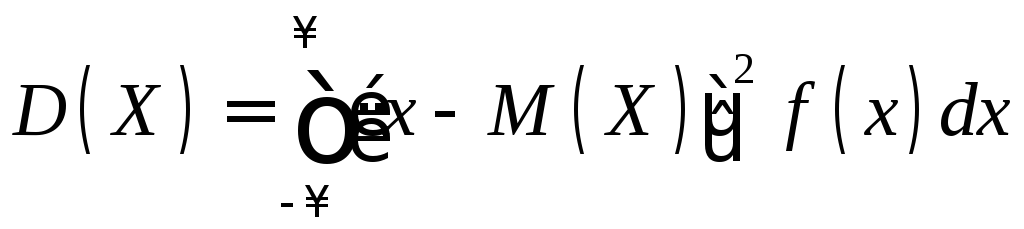Определение. Среднее кеадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

.

Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

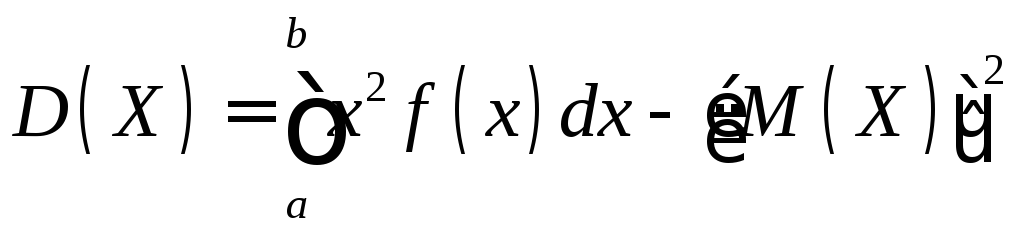, (11.2)

.

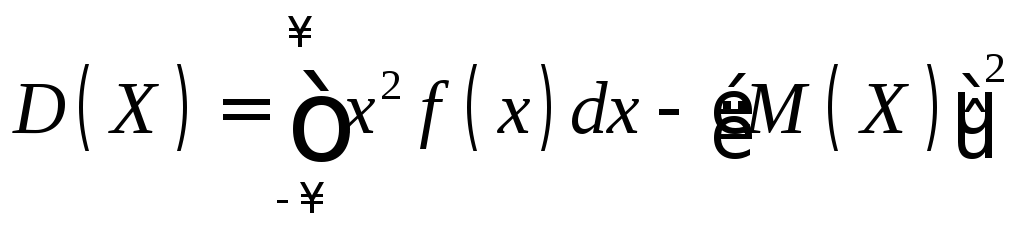Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения

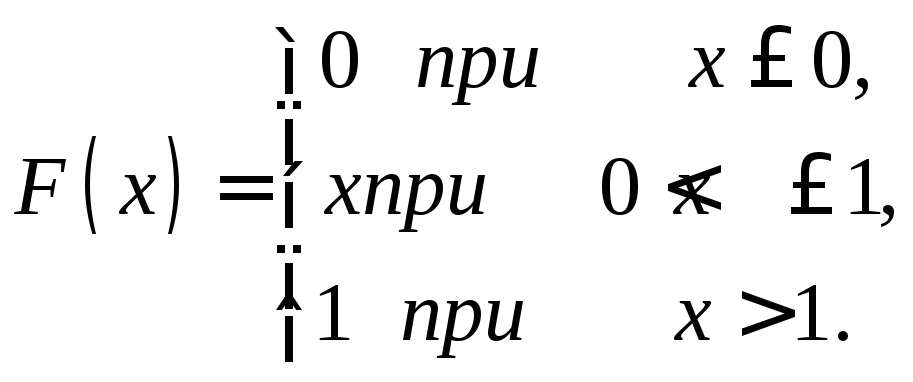
Решение. Найдем плотность распределения:

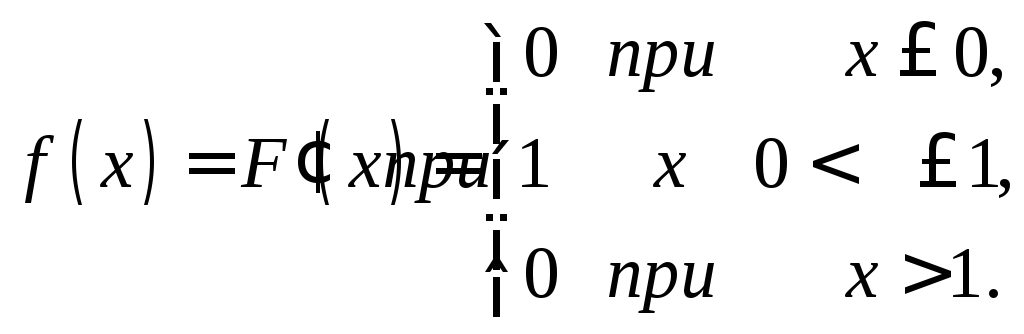
Найдем математическое ожидание по формуле (11.1):

.

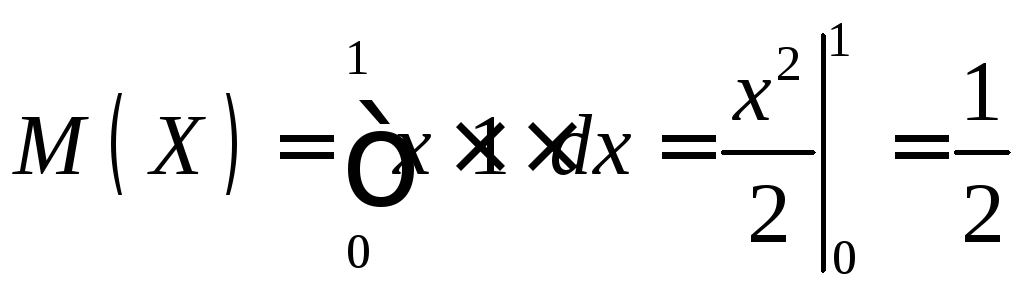Найдем дисперсию по формуле (11.2):

.

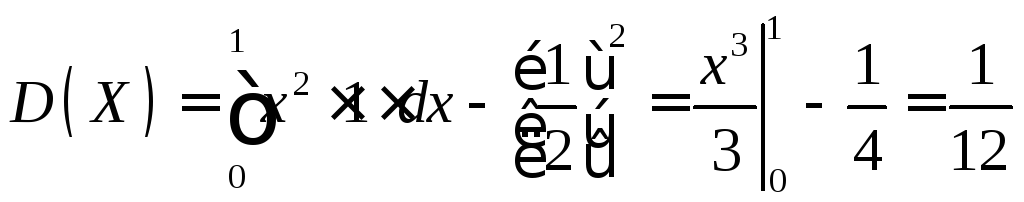Пример 2. Найти математическое ожидание н дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (а, b).

Решение. Найдем математическое ожидание X по формуле (11.1), учитывая, что плотность равномерного распределения f(x) = 1/(b – a)

.

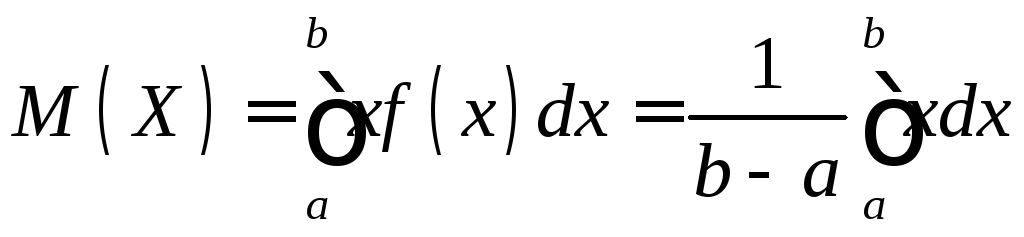Выполнив элементарные преобразования, получим

.

Найдем дисперсию X по формуле (11.2):

.

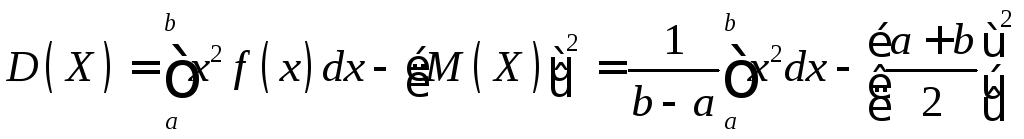Выполнив элементарные преобразования, получим

.

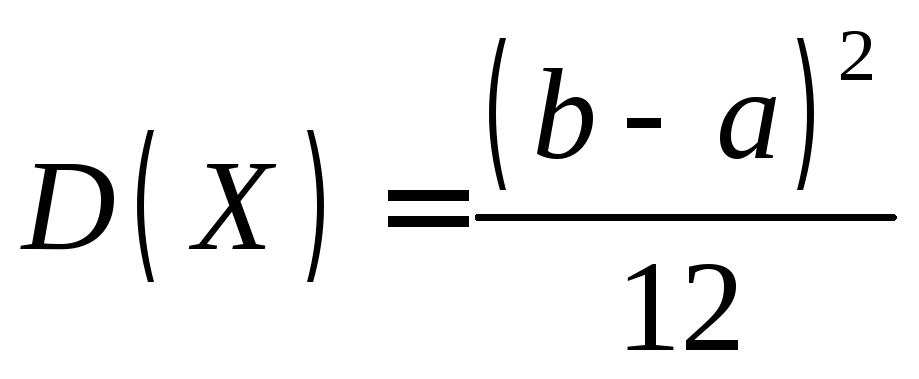Замечание 3. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0, 1), т.е. если а = 0, b = 1, как следует из примера 2, соответственно равны M(R) =1/2, D(R) = 1/12. Этот же результат был получен в примере 1 по заданной функции распределения случайной величины R.

Определение. Модой д.с.в. Х называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями, обозначается через М₀Х. Для н.с.в. М₀Х – точка максимума (локального) плотности f(x).

Если мода единственна, то распределение с.в. называют унимодальным, в противном случае – полимодальным (рис. 11.1).

Определение. Медианой М_еХ н.с.в. Х называется такое ее значение х_р, для которого

, (11.3)

то есть одинаково вероятно, окажется ли с.в. Х меньше х_р или больше х_р (рис. 11.1).

С помощью функции распределения F(x) равенство (11.3) можно записать в виде F(М_еХ) = 1 – F(М_еХ). Отсюда F(М_еХ) = 1/2.

Для д.с.в. медиана обычно не определяется.

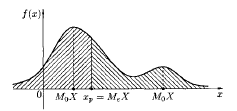
Рис. 11.1

Математическое ожидание и дисперсия являются частными случаями следующих более общих понятий – моментов с.в.

Определение. Начальным моментом порядка k с.в. Х называется м.о. k-й степени этой величины, обозначается через v_k.

Таким образом, по определению v_k = M[X^k]. Для д.с.в. начальный момент выражается суммой

,

а для н.с.в. – интегралом

.

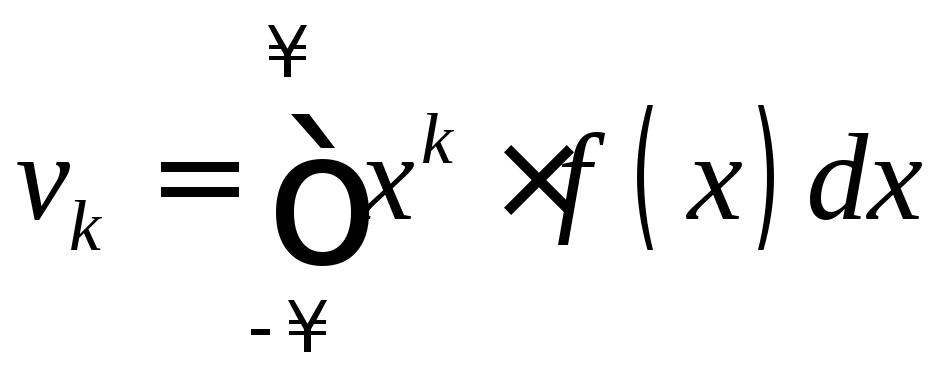В частности, v₁ = M[X], то есть начальный момент первого порядка есть м.о.

Определение. Центральным моментом порядка k с.в. Х называется м.о. величины (X – M[X])^k, обозначается через _k.

Таким образом, по определению _k = М(X – M[X])^k. В частности, ₂ = D[X], то есть центральный момент второго порядка есть дисперсия, ₁ = М(X – M[X]) = 0.

Для д.с.в. центральный момент равен

,

а для н.с.в.:

.

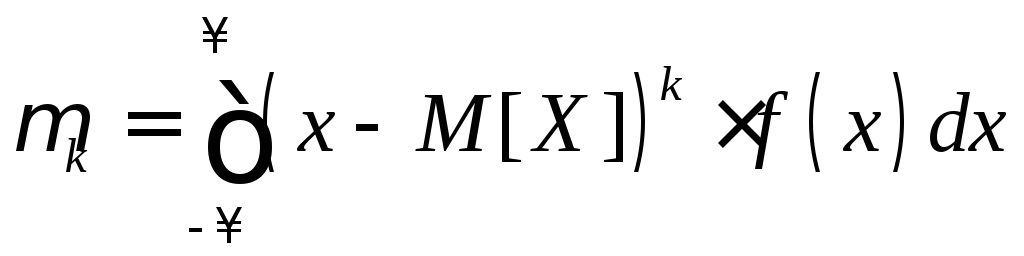Среди моментов высших порядков для н.с.в. особое значение имеют центральные моменты 3-го и 4-го порядков, называемые соответственно коэффициентами асимметрии и эксцесса.

Определение. Коэффициентом асимметрии («скошенности») А с.в. Х называется величина

.

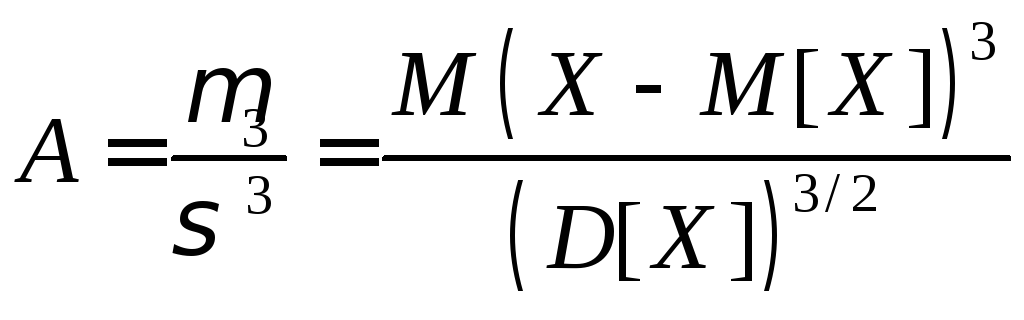Если А > 0, то кривая распределения более полога справа от М₀Х (рис. 11.2). Если А < 0, кривая распределения более полога слева от М₀Х (рис. 11.3).

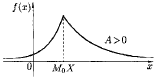
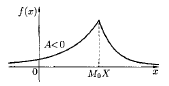
Рис. 11.2 Рис. 11.3

Определение. Коэффициентом эксцесса («островершинности») Е с.в. Х называется величина

.

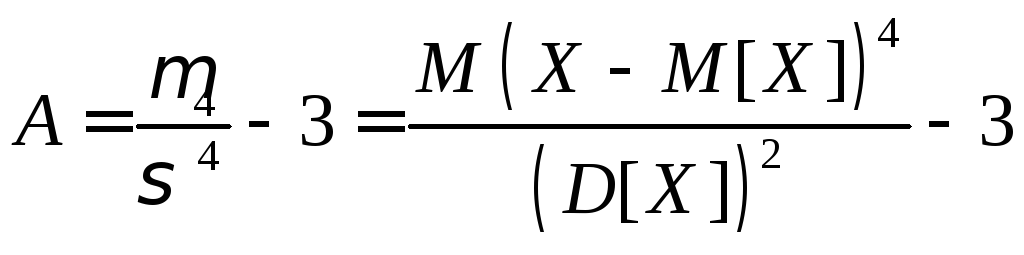Величина Е характеризует островершинность или плосковершинность распределения. Для нормального закона распределения А = 0, Е = 0; остальные распределения сравниваются с нормальным: если E > 0 – более островершинные, а распределения «плосковершинные» имеют E < 0 (рис. 11.4).

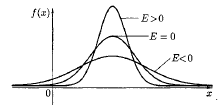
Рис. 11.4

Кроме рассмотренных выше числовых характеристик с.в., в приложениях используются так называемые квантили.

Определение. Квантилью уровня р с.в.Х называется решение уравнения

,

где р – некоторое число, 0< p < 1.

Квантили х_0,25, х_0,5, х_0,75 имеют свои названия: нижняя квантиль, медиана (М_еХ = х_0,5), верхняя квантиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0,25 (рис. 11.5).

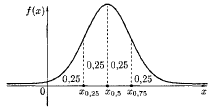
Рис. 11.5