1.5. Алгебра событий

Определение. Назовем алгеброй событий любое множество F с выделенной в нем совокупностью подмножеств М, такое что:

а) вместе с подмножеством А в М входит дополнение ,

б) вместе с любой счетной совокупностью подмножеств А₁, А₂, …, A_n, ... в М входит их объединение .

В силу равенства

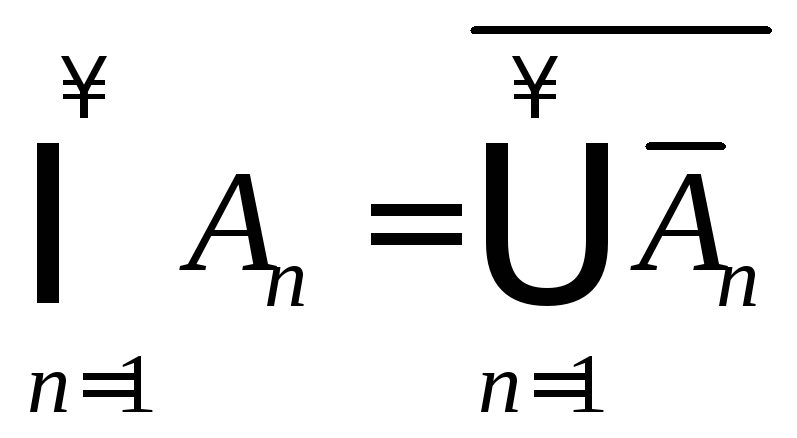
отсюда следует, что вместе с любой счетной совокупностью подмножеств А₁, А₂, …, A_n, ... в М входит их пересечение .

Если множество F конечно, условие б) можно заменить более простым условием б'): вместе с подмножествами А и В в М входит их объединение.

Определение. Объединение двух подмножеств А и В из совокупности М называется суммой соответствующих событий и обозначается А + В. Событие А + В происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В.

В более общем случае объединением или суммой событий А_k называется событие A, которое означает появление хотя бы одного из событий А_k.

Определение. Пересечение подмножеств А и В из совокупности М называется произведением соответствующих событий и обозначается АВ. Событие АВ происходит тогда и только тогда, когда происходят оба события А и В.

В более общем случае пересечением или произведением событий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

.

Определение. Если АВ = , события А и В называются несовместными, а если АВ   – совместными.

Определение. События А и В называются противоположными, если подмножества А и В взаимно дополнительны в М. Пишут .

Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие. Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

Определение. Если А  В, где А  М и В  М, то говорят, что событие В – следствие события А или что А влечет за собой В.

Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

Определение. Выбор элемента х в F назовем испытанием. Если х  А, А  М, то скажем, что при этом испытании произошло событие А. Если рассматриваемое событие произошло, то поставим ему в соответствие цифру 1, а если не произошло – поставим 0. Используя данные выше определения, получим следующие таблицы операций над событиями:

	А + В					АВ
В А	0	1			В А	0	1			А
0	0	1			0	0	0			0	1
1	1	1			1	0	1			1	0

Определение. Разностью событий А и В называется событие С, которое происходит тогда и только тогда, когда происходит событие А, но не происходит событие В.

Определение. Дополнительным к событию А называется событие , означающее, что событиеА не происходит.

Операции над событиями удобно иллюстрировать диаграммами Эйлера – Венна (рис. 2).

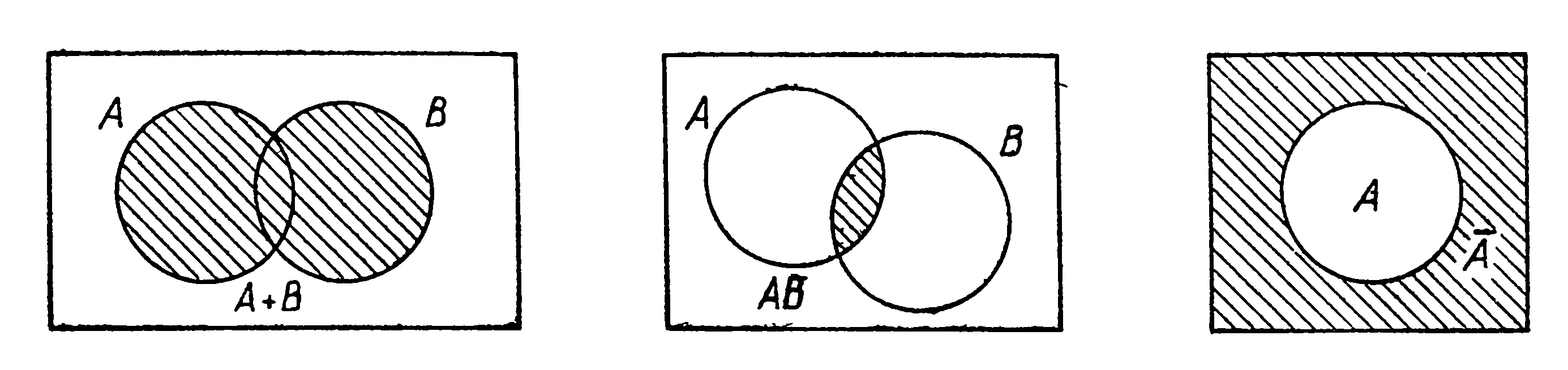
а) б) в)

Рис. 2

Пример. Событие А означает, что хотя бы одна пуля при четырех выстрелах попадает в цель. Что означает событие ?

Решение. Событие означает, что ни одна из четырех пуль не попала в цель.

Пример. Известно, что события А и В произошли, а событие С не произошло. Определим, произошло или не произошло событие .

Решение. Используя таблицы операций над событиями получим:

А	В	С
1	1	0	0	1	1	1	1

Значит, событие произошло.

Пример. Доказать, что .

Доказательство. Воспользуемся тем, что событие (см. рис. 2,б). Тогда. Но событие, так как событие- достоверное. Таким образом,.

Пример. Из 25 студентов группы 20 человек увлекаются спортом (событие А), 9 – музыкой (событие В), 6 – музыкой и спортом (событие А В). Построим диаграмму Эйлера — Венна и покажем, что означают события .

Решение. Строим диаграмму Эйлера — Венна (рис. 3).

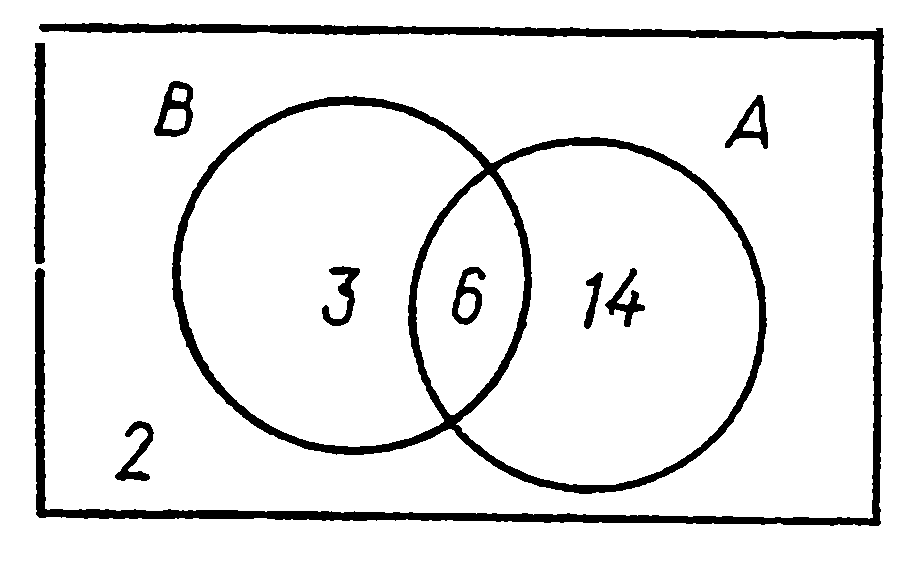
Круги обозначают события А и В, пересечение кругов – событие АВ. Пересечению кругов соответствует число студентов, увлекающихся музыкой и спортом, т.е. 6 человек. События означают соответственно, что 14 студентов увлекаются только спортом, а 3 – только музыкой. Значит, музыкой или спортом увлекаются 23 студента, и потому событие означает, что только двое из студентов не имеют этих увлечений.

Исходя из этих общих понятий, можно дать определение вероятности.