4.3. Локальная и интегральная теоремы Муавра-Лапласа

В тех случаях, когда число испытаний n велико, а вероятность р не близка к нулю (р  0, р  1), для вычисления биномиальных вероятностей используют теоремы Муавра – Лапласа. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытаний достаточно велико.

(Напомним, что функцию (х) называют асимптотическим приближением функции f(x), если ).

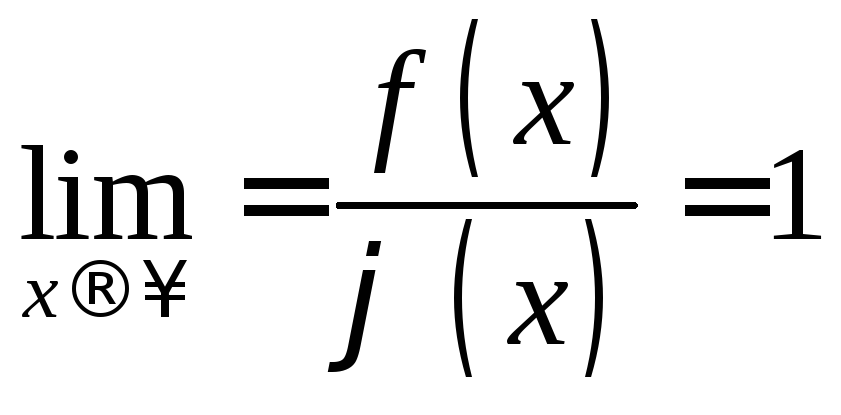Заметим, что для частного случая, а именно для р = 1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра-Лапласа.

Доказательство локальной теоремы Лапласа довольно сложно, поэтому приведем лишь формулировку теоремы и примеры, иллюстрирующие ее использование.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции

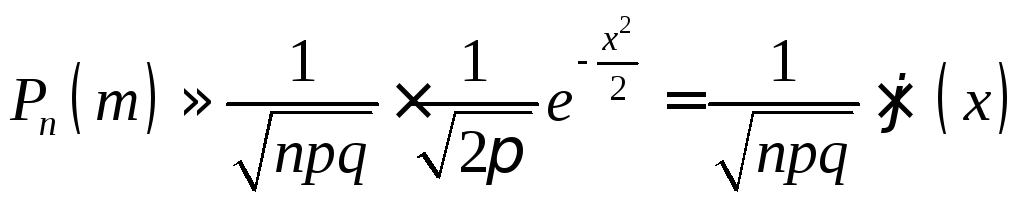, (4.6)

где 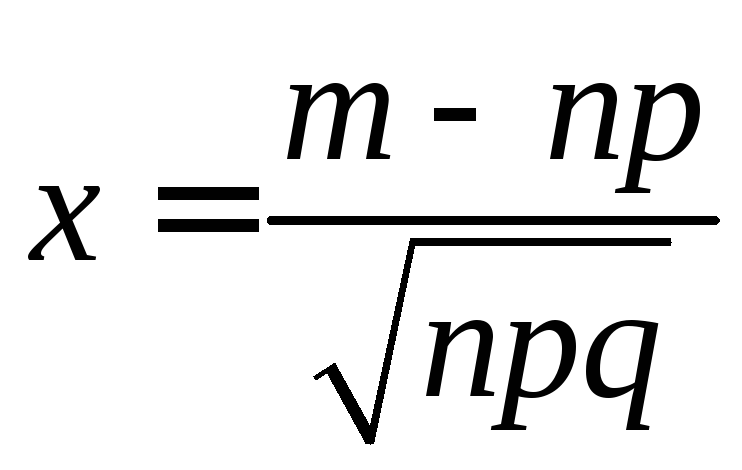. Выражение

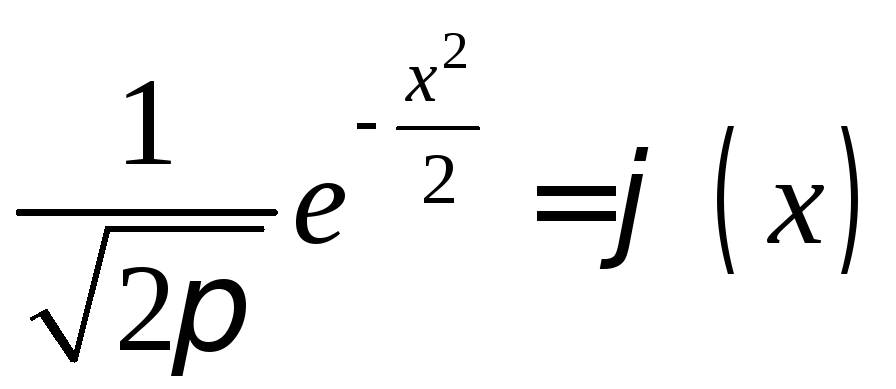(4.7)

называется функцией Гаусса, а ее график – кривой вероятностей (рис. 4.2).

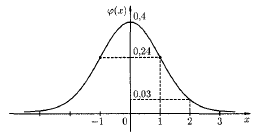
Рис. 4.2.

Для функции (х) составлены таблицы значений, соответствующие положительным значениям аргумента х. Пользуясь таблицей, следует учитывать, что:

а) функция (х) четная, то есть (- х) = (х);

б) при х  4 можно считать, что (х) = 0.

Для отрицательных значений аргумента пользуются теми же таблицами, так как функция (х) четна.

Пример. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение. По условию, n = 400; m = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа:

.

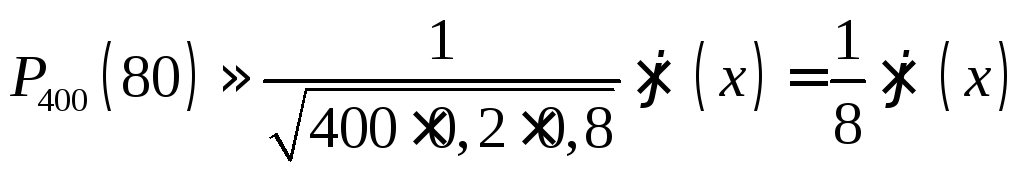Вычислим определяемое данными задачи значение х:

.

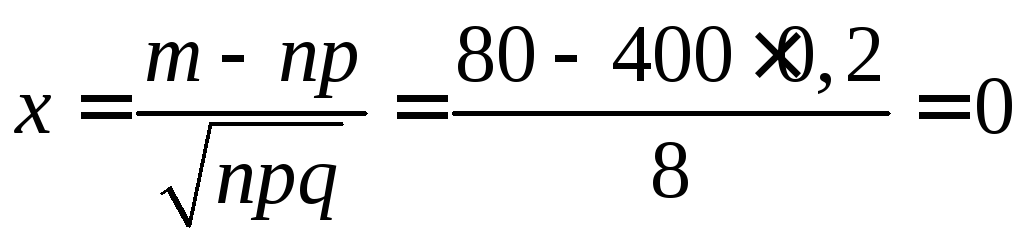По таблице приложения 1 находим (0) = 0,3989. Искомая вероятность

.

Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):

Р₄₀₀(80) = 0,0498.

Пример. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.

Решение. Здесь n = 200; m = 160; р = 0,7; q = 0,3. Применим фориулу (4.6). Имеем , следовательно,, учитывая, что(3,09)  0,0034, получаем .

Пример. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. По условию, n = 10; m = 8; р = 0,75; q = 0,25. Воспользуемся асимптотической формулой Лапласа:

.

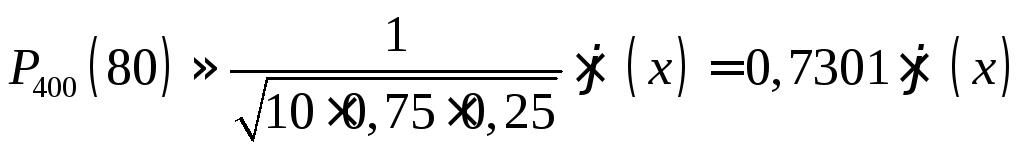Вычислим определяемое данными задачи значение х:

.

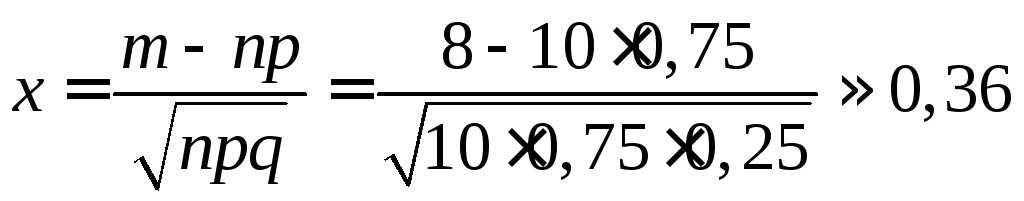По таблице приложения 1 находим (0,36) = 0,3739. Искомая вероятность

Р₁₀(8) = 0,73010,3739 = 0,273.

Формула Бернулли приводит к иному результату, а именно Р₁₀(8) = 0,282. Столь значительное расхождение ответов объясняется тем, что в настоящем примере n имеет малое значение (формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях n).

Интегральная теорема Лапласа. Вновь предположим, что производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). В тех случаях, когда требуется вычислить верятностьтого, что в n независимых испытаниях событие А появится не менее k₁ раз, но не более k₂ раз, то есть P_n(k₁  m  k₂) или P_n(k₁; k₂), используют интегральную теорему Муавра-Лапласа (является частным случаем более общей теоремы – центральной предельной теоремы).

Теорема (Интегральная теорема Муавра-Лапласа). Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁  m  k₂) того, что событие А появится в n испытаниях от k₁ до k₂ раз, может быть найдена по приближенной формуле

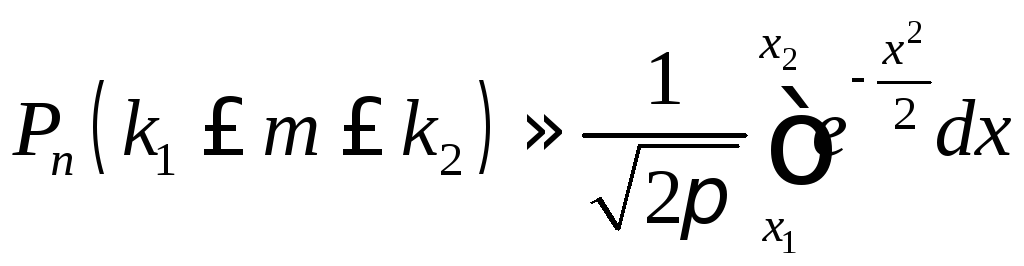, (4.8)

где 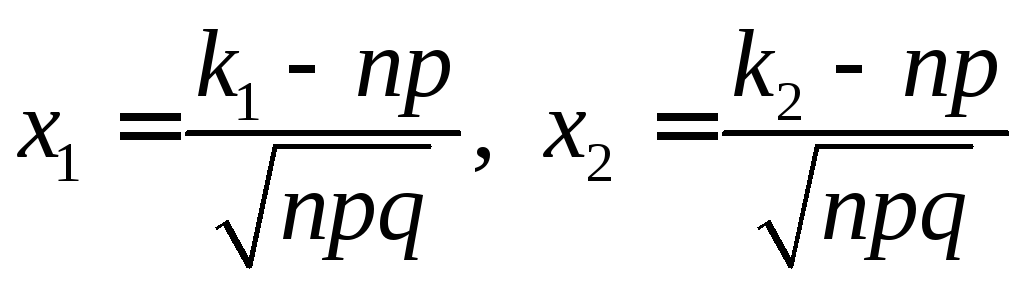. Равенство (4.8) тем точнее, чем большеn.

Используя функцию Гаусса (4.7), равенство (4.8) можно записать в виде

.

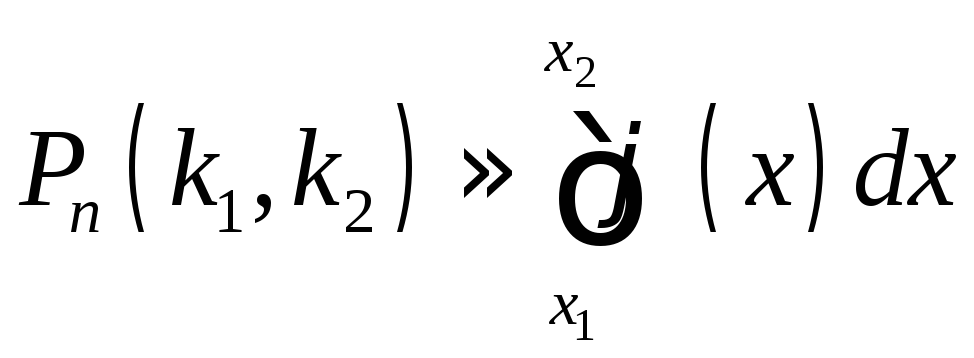При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как этот неопределенный интеграл не выражается через элементарные функции. Для упрощения вычислений, при использовании формулы (4.8), вводят специальную функцию

, (4.9)

называемую нормированной функцией Лапласа.

Функция (4.9) нечетна:

.

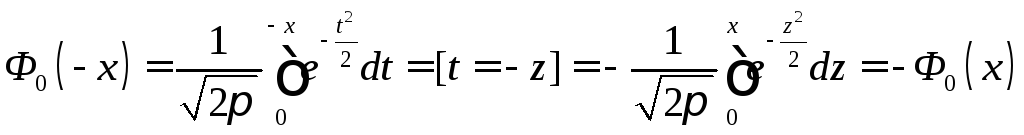При х  5 можно считать, что Ф₀(х) = 0,5, график функции Ф₀(х) приведен на рис. 4.3.

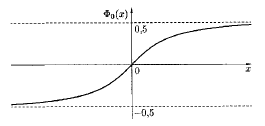
Рис. 4.3.

Выразим правую часть равенства (4.8) через функцию Лапласа (4.9):

.

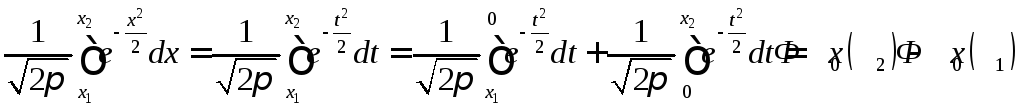Равенство (4.8) принимает вид

, (4.10)

где .

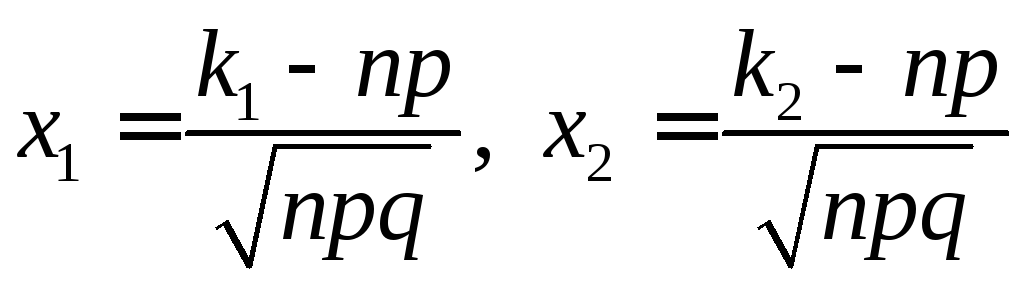Формулу (4.10) обычно используют на практике. Наряду с нормированной функцией Лапласа (4.9) использую функцию

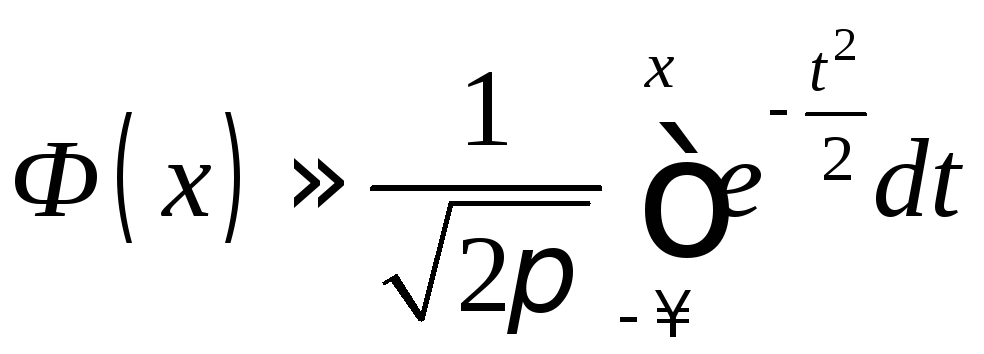, (4.11)

называемую также функцией Лапласа. Для нее справедливо равенство Ф(-х) + Ф(х) = = 1. Она связана с функцией Ф₀(х) формулой

. (4.12)

Имеются таблицы приближенных значений функций Ф₀(х) и Ф(х) (интеграл не берется в элементарных функциях), которые приводятся в большинстве учебников по теории вероятностей.

Приближенную формулу для вычисления вероятности P_n(k₁  m  k₂) (4.8) можно записатьв виде

, (4.13)

где .

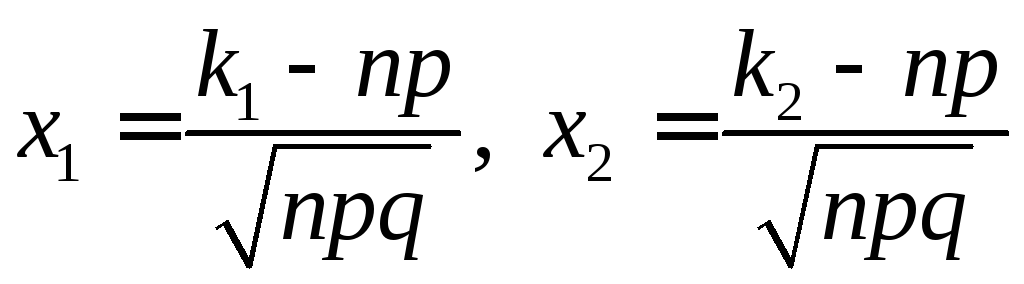Приведем примеры, иллюстрирующие применение интегральной теоремы Лапласа.

Пример. Проверкой установлено, что цех в среднем выпускает 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого цеха. Если среди них окажется более 10 изделий не высшего сорта, то вся партия изделий бракуется, то есть возвращается в цех. Какова вероятность того, что партия будет принята?

Решение. Здесь n = 200, p = 0,04 (вероятность негодного изделия), q = 0,96. Вероятность принятия всей партии, то есть P₂₀₀(0  m  10), можно найти по формуле (4.13); здесь k₁ =0, k₂ = 10. Находим, что

, .

.

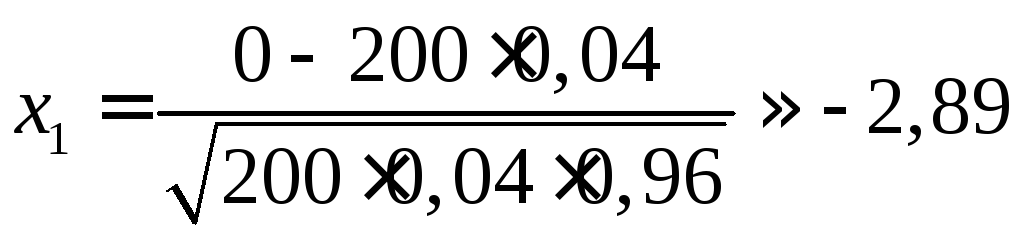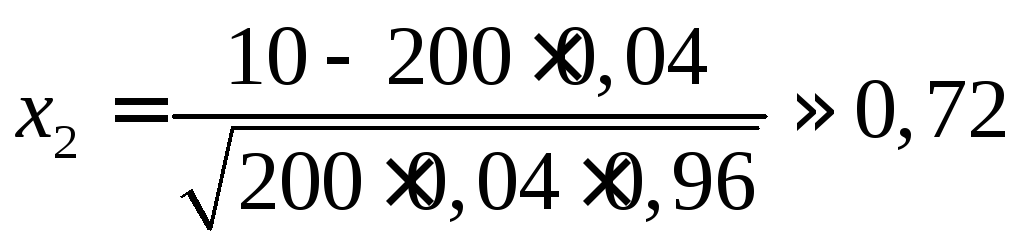Заметим, что

.

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию, р = 0,2; q = 0,8; n = 400; k₁ = 70; k₂ = 100. Воспользуемся интегральной теоремой Лапласа:

Р₄₀₀(70, 100)  Ф(х₂) – Ф(х₂).

Вычислим нижний и верхний пределы интегрирования:

; .

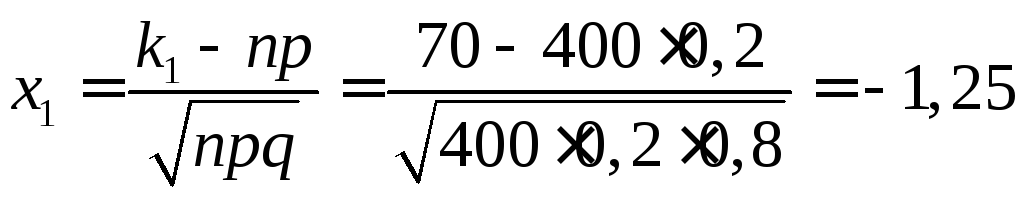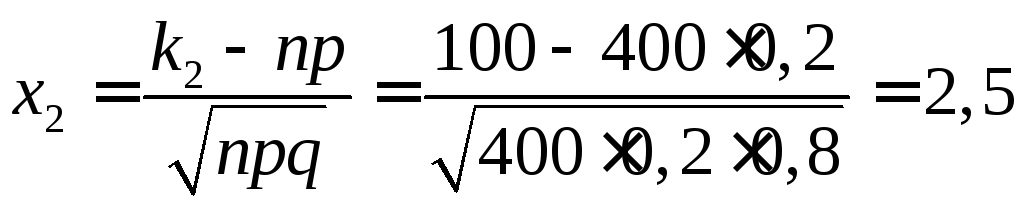Таким образом, имеем

Р₄₀₀(70, 100) = Ф(2,5) – Ф(–1,25) = Ф(2,5) + Ф(1,25).

По таблице приложения находим:

Ф(2,5) = 0,4938; Ф(1,25) = 0,3944.

Искомая вероятность

Р₄₀₀(70, 100) = 0,4938 + 0,3944 = 0,8882.

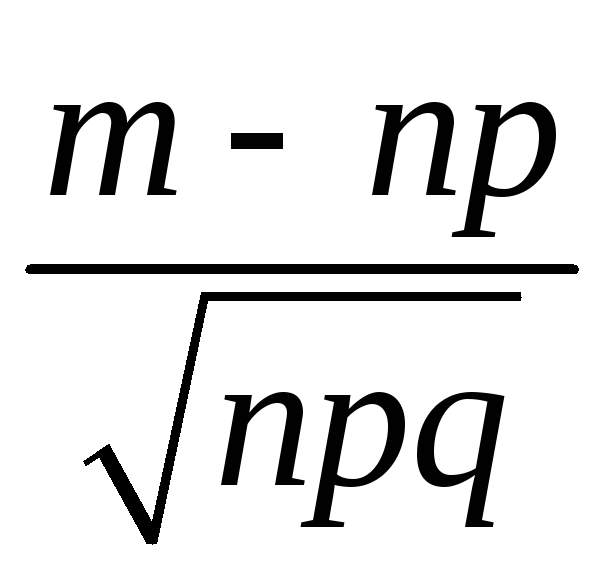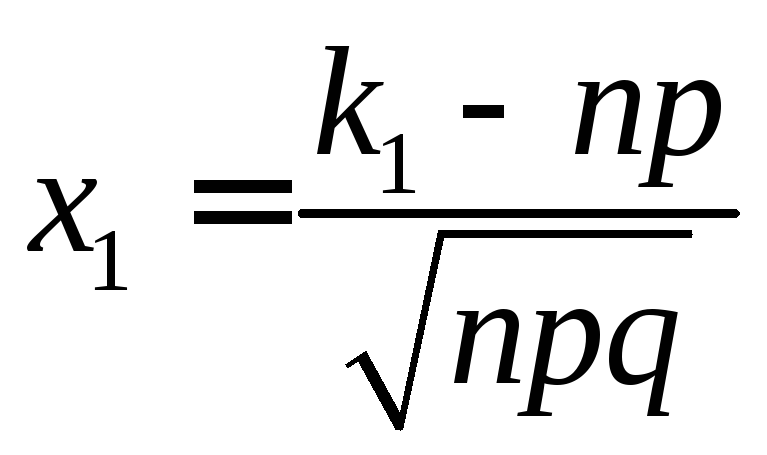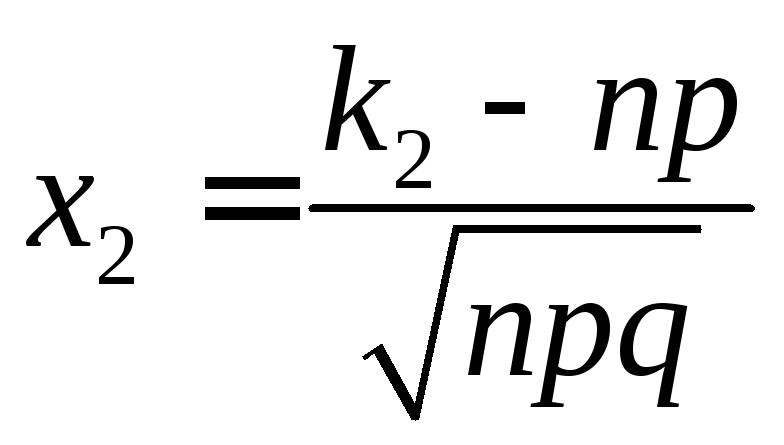Замечание. Обозначим через m число появлений события А при n независимых испытаниях, в каждом из которых вероятность наступления события А постоянна и равна р. Если число m изменяется от k₁ до k₂, то дробь изменяется отдо. Следовательно, интегральную теорему Лапласа можно записать и так:

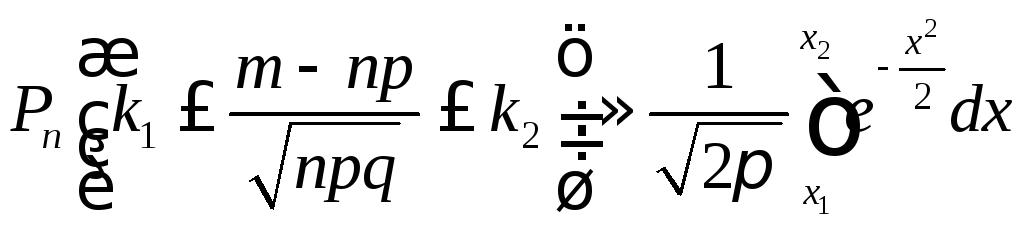. (4.14)

Эта форма записи используется ниже.