Лекция №3 следствия теорем сложения и умножения

3.1. Теорема сложения вероятностей совместных событий

Была рассмотрена теорема сложения для несовместных событий. Рассмотрим теорему сложения для совместных событий.

Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример. А – появление четырех очков при бросании игральной кости; В – появление четного числа очков. События А и В – совместные.

Пусть события А и В совместны, причем даны вероятности этих событий и вероятность их совместного появления. Как найти вероятность события А + В, состоящего в том, что появится хотя бы одно из событий А и В? Ответ на этот вопрос дает теорема сложения вероятностей совместных событий.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р(А + В) = Р(А) + Р(В) – Р(АВ).

Доказательство. Поскольку события А и В, по условию, совместны, то событие А + В наступит, если наступит одно из следующих трех несовместных событий: илиАВ. По теореме сложения вероятностей несовместных событий,

. (3.1)

Событие А произойдет, если наступит одно из двух несовместных событий: илиАВ. По теореме сложения вероятностей несовместных событий имеем

.

Отсюда

. (3.2)

Аналогично имеем

Отсюда

. (3.3)

Подставив (3.2) и (3.3.) в (3.1), окончательно получим

Р(А + В) = Р(А) + Р(В) – Р(АВ). (3.4)

В справедливости формул можно наглядно убедиться на рис. 3.1.

Рис. 3.1

Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми.

Для независимых событий

Р(А + В) = Р(А) + Р(В) – Р(А)Р(В);

для зависимых событий

Р(А + В) = Р(А) + Р(В) – Р(А)Р_А(В).

Замечание 2. Если события А и В несовместны, то их совмещение есть невозможное событие и, следовательно, Р(АВ) = 0. Формула (3.4) для несовместных событий принимает вид

Р(А + В) = Р(А) + Р(В).

Мы вновь получили теорему сложения для несовместных событий. Таким образом, формула (3.4) справедлива как для совместных, так и для несовместных событий.

Пример. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: р₁ = 0,7; р₂ = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы.

Вероятность события АВ (оба орудия дали попадание)

Р(АВ) = Р(А)Р(В) = 0,70,8 = 0,56.

Искомая вероятность

Р(А + В) = Р(А) + Р(В) – Р(АВ) = 0,7 + 0,8 – 0,56 = 0,94.

Замечание 3. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой Р = 1 – q₁q₂. В самом деле, вероятности событий, противоположных событиям А и В, т.е. вероятности промахов, таковы:

q₁ = 1 – р₁ = 1 – 0,7 = 0,3; q₂ = 1 – p₂= 1 – 0,8 = 0,2.

Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна

Р = 1 – q₁q₂ = 1 – 0,30.2 = 0,94.

Как и следовало ожидать, получен тот же результат.

Можно получить формулу вероятности суммы трех и большего числа совместных событий; для трех событий она имеет вид

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС). (3.5)

Справедливость равенства поясняет рис. 3.2.

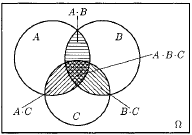
Рис. 3.2.

Проще, однако, найти вероятность суммы нескольких совместных событий P(S) = P(A₁ +A₂ + … +A_n), используя равенство , где- противоположно событиюS. Тогда . Этот прием можно использовать и при решении задач.

Пример. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?

Решение. Введем события: А – появление шестерки на первой кости, В – на второй кости. Тогда А + В – появление хотя бы одной шестерки при бросании костей события А и В совместные.

.

Следовательно, . Или то же самое можно получить по формуле (3.4):.