Неравенство Коши — Буняковского — Шварца и неравенство треугольника

В данном выше определении угла остался один пробел: для того, чтобы был определён, необходимо, чтобы выполнялось неравенствоЭто неравенство действительно выполняются в произвольном евклидовом пространстве, оно называетсянеравенством Коши — Буняковского — Шварца. Из этого неравенства, в свою очередь, следует неравенство треугольника: Неравенство треугольника, вместе с перечисенными выше свойствами длины, означает, что длина вектора являетсянормой на евклидовом векторном пространстве, а функция задаёт на евклидовом пространстве структуруметрического пространства (эта функция называется евклидовой метрикой). В частности, расстояние между элементами (точками) икоординатного пространствазадаётся формулой

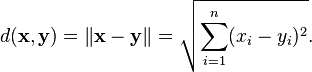
48. Ортонормированная система векторов евклидового пространства

Ортонормированные базисы

Ортонормированный базис в евклидовом (векторном) пространстве — это базис, состоящий из попарно ортогональных векторов единичной нормы. Ортонормированные базисы наиболее удобны для вычислений. Так, например, скалярное произведение векторов с координатами ив ортонормированном базисе можно вычислять по формулеВ любом евклидовом пространстве существует ортонормированный базис. Выбрав в двух евклидовых пространствах ортонормированные базисы и переведя один из них в другойлинейным отображением, можно доказать, что любые два евклидовых пространства одинаковой размерности изоморфны (в частности, -мерное евклидово пространство изоморфносо стандартным скалярным произведением).

49. Линейный оператор и его матрица. Линейное преобразование в координатах.

Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(x)=n  и пусть e₁,  e₂, ..., e_n - базис в X. Обозначим через A e₁ = (a₁₁,...,a_n1), ... , A e_n = (a_1n,...,a_nn) образы базисных векторов e₁,  e₂, ..., e_n .

Матрица

Столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно каждая  квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения

с одной стороны, связывают координаты образа y = A x с координатами прообраза X, с другой стороны,  описывают действие оператора, заданного матрицей A.

Линейное преобразование в координатах

Рассмотрим линейное преобразование-мерного линейного пространства, заданное в некотором базисеМатрицей (10.2) Координаты вектораИ его образаИзвестны: (10.3) Зависимость между координатами векторов х и у выражается формулами (10.4) Формулы (10.4) можно записать в матричном виде гдеОпределяется формулой (10.2), а-формулами (10.5) Если переменныеСвязаны с переменнымиФорму Лами (10.4), то будем говорить, что задано линейное однородное преобразование переменных с матрицей, переводящее переменныеВ переменные . Оно обладает теми же свойствами, что и линейное преобразование -мерного линейного пространства. Линейное однородное преобразование переменных (10.4) или (10.5) называется невырожденным, если Замечание. При рассмотрении линейных преобразований (линейных операторов) пользуются и другими обозначениями. ЕслиГде Линейное преобразование (линейный оператор) с матрицей А в некотором базисе, то пишутУсловия 1) и 2), определяющие линейное преобразование, мож Но записать в виде

50. Матрица оператора в различных базисах. Подобные матрицы

Связь между матрицами одного и того же линейного оператора в разных базисах

     Если в базисе линейный операторимеет матрицуA, в базисе - матрицуB, а S - матрица перехода от первого базиса ко второму, то

Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что:

Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных координатных системах; при этом матрица Р является матрицей перехода от одной системы к другой.

Если две матрицы подобны, то говорят, что одна из матриц может быть получена преобразованием подобия из другой. Если при этом одна из матриц диагональная, то про вторую матрицу говорят, что она может быть диагонализована.

51. Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора

Определитель стоящий в левой части уравнения (4) образует многочлен n-ой степени относительно , он называется характеристическим многочленом, а уравнение (4) характеристическим уравнением линейного оператора  .

Пусть линейный оператор, действующий в линейном пространстве.

Число называетсясобственным значением, а ненулевой вектор соответствующимсобственным вектором линейного оператора , если они связаны между собой соотношением.

52. Собственные векторы и значение симметричной матрицы.

Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Пусть —линейное пространство над полем ,—линейное преобразование.

Собственным вектором линейного преобразования называется такой ненулевойвектор , что для некоторого

Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. она равна её транспонированной матрице: